19.2: Momentum angular alrededor de un punto para una partícula

Momentum angular para una partícula puntual

Considera una partícula puntiforme de masa m que se mueve con una velocidad\(\overrightarrow{\mathbf{V}}\) (Figura 19.1) con impulso\( \overrightarrow{\mathbf{p}}=m \overrightarrow{\mathbf{v}}\).

Figura\(\PageIndex{1}\): Una partícula puntiforme y su momento angular alrededor de S.Considere un punto\(S\) ubicado en cualquier lugar del espacio. Dejar\(\overrightarrow{\mathbf{r}}_{S}\) denotar el vector desde el punto\(S\) hasta la ubicación del objeto.

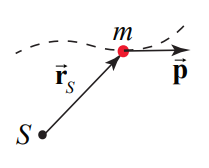
Definir el momento angular\(\overrightarrow{\mathbf{L}}_{s}\) alrededor del punto\(S\) de una partícula puntiforme como el producto vectorial del vector desde el punto\(S\) hasta la ubicación del objeto con el momento de la partícula,

\[\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{r}}_{S} \times \overrightarrow{\mathbf{p}} \nonumber \]

Las unidades SI derivadas para el momento angular son\(\left[\mathrm{kg} \cdot \mathrm{m}^{2} \cdot \mathrm{s}^{-1}\right]=[\mathrm{N} \cdot \mathrm{m} \cdot \mathrm{s}]=[\mathrm{J} \cdot \mathrm{s}]\). No hay un nombre especial para este conjunto de unidades.

Debido a que el momento angular se define como un vector, comenzamos por estudiar su magnitud y dirección. La magnitud del momento angular alrededor\(S\) viene dada por

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=\left|\overrightarrow{\mathbf{r}}_{S}\right||\overrightarrow{\mathbf{p}}| \sin \theta \nonumber \]

donde\(θ\) está el ángulo entre los vectores y\(\overrightarrow{\mathrm{p}}\), y se encuentra dentro del rango\([0 \leq \theta \leq \pi]\) Análogamente a la magnitud del par, hay dos formas de determinar la magnitud del momento angular alrededor de S.

Figura\(\PageIndex{2}\): (a) Brazo de momento. b) Componente perpendicular del impulso.

Definir el brazo de momento\(r_{S}^{\perp}\),, (Figura\(\PageIndex{1a}\)), como la distancia perpendicular desde el punto\(S\) a la línea definida por la dirección del momento. Entonces

\[r_{S}^{\perp}=\left|\overrightarrow{\mathbf{r}}_{S}\right| \sin \theta \nonumber \]

De ahí que la magnitud del momento angular sea el producto del brazo de momento con la magnitud del momento,

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=r_{s}^{\perp}|\overrightarrow{\mathbf{p}}| \nonumber \]

Alternativamente, vamos a\(|\overrightarrow{\mathbf{p}}|\) denotar la magnitud de la componente del momento perpendicular a la línea definida por la dirección del vector\(\overrightarrow{\mathbf{r}}_{S}\). A partir de la geometría mostrada en la Figura\(\PageIndex{1b}\),

\[p_{S}^{\perp}=|\overrightarrow{\mathbf{p}}| \sin \theta \nonumber \]

Así, la magnitud del momento angular es el producto de la distancia desde\(S\) la partícula con\(p_{S}^{\perp}\),

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=\left|\overrightarrow{\mathbf{r}}_{s}\right| p_{s}^{\perp} \nonumber \]

Regla de la mano derecha para la dirección del momento angular

Definiremos la dirección del momento angular alrededor del punto\(S\) mediante una regla de la mano derecha. Dibuja los vectores\(\overrightarrow{\mathbf{r}}_{S} \text { and } \overrightarrow{\mathbf{p}}\) para que sus colas se toquen. Después dibuja un arco partiendo del vector\(\overrightarrow{\mathbf{r}}_{S}\) y terminando sobre el vector\(\overrightarrow{\mathrm{p}}\). (Hay dos arcos de este tipo; elige el más corto.) Este arco es en el sentido de las agujas del reloj o en sentido antihorario. Enrilla los dedos de tu mano derecha en la misma dirección que el arco. Tu pulgar derecho apunta en la dirección del momento angular.

Figura 19.3 La regla de la derecha para determinar la dirección del momento angular alrededor\(S\).

Recuerde que, como en todos los productos vectoriales, la dirección del momento angular alrededor\(S\) es perpendicular al plano formado por\(\overrightarrow{\mathbf{r}}_{S} \text { and } \overrightarrow{\mathbf{p}}\).

Ejemplo\(\PageIndex{1}\): Angular Momentum: Constant Velocity

Una partícula de masa\(m=2.0 \mathrm{kg}\) se mueve como se muestra en la Figura 19.4 con una velocidad uniforme\(\overrightarrow{\mathbf{v}}=3.0 \mathrm{m} \cdot \mathrm{s}^{-1} \hat{\mathbf{i}}+3.0 \mathrm{m} \cdot \mathrm{s}^{-1} \hat{\mathbf{j}}\). En el tiempo t, la partícula pasa por el punto (2.0 m, 3.0 m). Encuentra la dirección y la magnitud del momento angular alrededor del punto\(S\) (el origen) en el tiempo t.

Figura 19.4 Ejemplo 19.4

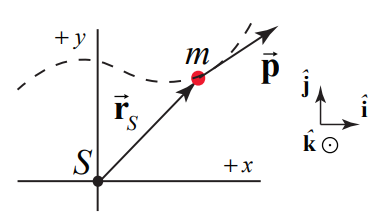
Solución

Elija coordenadas cartesianas con vectores unitarios mostrados en la figura anterior. El vector desde el punto\(S\) hasta la ubicación de la partícula es\(\overrightarrow{\mathbf{r}}_{S}=2.0 \mathrm{m} \hat{\mathbf{i}}+3.0 \mathrm{m} \hat{\mathbf{j}}\). El vector\(\overrightarrow{\mathbf{L}}_{O}\) de momento angular de la partícula sobre el origen\(S\) viene dado por:

\ [\ begin {alineado}
\ overrightarrow {\ mathbf {L}} _ {S} &=\ overrightarrow {\ mathbf {r}} _ {S}\ veces\ overrightarrow {\ mathbf {p}} =\ overrightarrow {\ mathbf {r}} _ {S}\ veces m\ overrightarrow {\ mathbf {v}}\
& =( 2.0\ mathrm {m}\ hat {\ mathbf {i}} +3.0\ mathrm {m}\ hat {\ mathbf {j}})\ times (2\ mathrm { kg})\ izquierda (3.0\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ hat {\ mathbf {i}} +3.0\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ hat {\ mathbf {j}}\ derecha)\\
&=0+12\ mathrm {kg}\ cdot\ mathrm {m} ^ ^ 2}\ cdot\ mathrm {s} ^ {-1}\ sombrero {\ mathbf {k}} -18\ mathrm {kg}\ cdot\ mathrm {m} ^ {2}\ cdot\ mathrm {s} ^ {-1} (-\ hat {\ mathbf {k}}) +\ overrightarrow {\ mathbf {0}}\\
&=-6\ mathrm {kg}\ cdot\ mathrm {m} ^ {2}\ cdot\ mathrm {s} ^ {-1}\ sombrero {\ mathbf {k}}
\ end {alineado}\ nonumber\]

En lo anterior,\(\overrightarrow{\mathbf{i}} \times \overrightarrow{\mathbf{j}}=\overrightarrow{\mathbf{k}}, \overrightarrow{\mathbf{j}} \times \overrightarrow{\mathbf{i}}=-\overrightarrow{\mathbf{k}}, \quad \overrightarrow{\mathbf{i}} \times \overrightarrow{\mathbf{i}}=\overrightarrow{\mathbf{j}} \times \overrightarrow{\mathbf{j}}=\overrightarrow{\mathbf{0}}\) se utilizaron las relaciones.

Ejemplo\(\PageIndex{2}\): Angular Momentum and Circular Motion

Una partícula de masa m se mueve en un círculo de radio R alrededor del eje z en el plano x-y definido por z = 0 con velocidad angular\(\vec{\omega}=\omega_{z} \hat{\mathbf{k}}, \omega_{z}>0\), (Figura 19.5). Encuentra la magnitud y la dirección del momento angular en\(\overrightarrow{\mathbf{L}}_{s}\) relación con el punto que\(S\) se encuentra en el centro de la órbita circular, (el origen).

Figura 19.5 Ejemplo 19.2

Solución

La velocidad de la partícula viene dada por\(\overrightarrow{\mathbf{v}}=R \omega_{z} \hat{\boldsymbol{\theta}}\). El vector desde el centro del círculo (el punto\(S\)) hasta el objeto viene dado por\(\overrightarrow{\mathbf{r}}_{S}=R \hat{\mathbf{r}}\). El momento angular alrededor del centro del círculo es el producto vectorial

\[\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{r}}_{s} \times \overrightarrow{\mathbf{p}}=\overrightarrow{\mathbf{r}}_{S} \times m \overrightarrow{\mathbf{v}}=R m v \hat{\mathbf{k}}=R m R \omega_{z} \hat{\mathbf{k}}=m R^{2} \omega_{z} \hat{\mathbf{k}}=I_{S} \vec{\omega} \nonumber \]

La magnitud es\(\left|\overrightarrow{\mathbf{L}}_{S}\right|=m R^{2} \omega_{z}\), y la dirección está en la\(+\hat{\mathbf{k}}\) dirección -dirección. Para la partícula, el momento de inercia alrededor del eje z es\(I_{S}=m R^{2}\), por lo tanto, el momento angular alrededor\(S\) es

\[\overrightarrow{\mathbf{L}}_{S}=I_{S} \vec{\omega} \nonumber \]

El hecho de que\(\overrightarrow{\mathbf{L}}_{s}\) esté en la misma dirección que la velocidad angular se debe a que el punto\(S\) se encuentra en el plano de movimiento.

Ejemplo\(\PageIndex{3}\): Angular Momentum About a Point along Central Axis for Circular Motion

Una partícula de masa m se mueve en un círculo de radio R con velocidad angular\(\vec{\omega}=\omega_{z} \hat{\mathbf{k}}, \omega_{z}>0\) alrededor del eje z - en un plano paralelo pero a una distancia h por encima del plano x-y (Figura 19.6). Encuentra la magnitud y la dirección del momento angular en\(\overrightarrow{\mathbf{L}}_{s}\) relación con el punto\(S\) (el origen).

Figura 19.6 Ejemplo 19.3

Solución

La forma más fácil de calcular\(\overrightarrow{\mathbf{L}}_{s}\) es usar coordenadas cilíndricas. Comenzamos por escribir los dos vectores\(\overrightarrow{\mathbf{r}}_{S} \text { and } \overrightarrow{\mathbf{p}}\) en coordenadas polares. Comenzamos con el vector desde el punto\(S\) (el origen) hasta la ubicación del objeto en movimiento,\(\overrightarrow{\mathbf{r}}_{S}=R \hat{\mathbf{r}}+h \hat{\mathbf{k}}\). El vector de momento es tangente a la órbita circular así\(\overrightarrow{\mathbf{p}}=m \overrightarrow{\mathbf{v}}=m R \omega_{z} \hat{\mathbf{\theta}}\). Usando el hecho de que\(\hat{\mathbf{r}} \times \hat{\boldsymbol{\theta}}=\hat{\mathbf{k}} \text { and } \hat{\mathbf{k}} \times \hat{\boldsymbol{\theta}}=-\hat{\mathbf{r}}\), el momento angular sobre el punto\(S\) es

\[\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{r}}_{S} \times \overrightarrow{\mathbf{p}}=(R \hat{\mathbf{r}}+h \hat{\mathbf{k}}) \times m R \omega_{z} \hat{\mathbf{\theta}}=m R^{2} \omega_{z} \hat{\mathbf{k}}-h m R \omega_{z} \hat{\mathbf{r}} \nonumber \]

Figura 19.7 Momento angular sobre el punto S

La magnitud de\(\overrightarrow{\mathbf{L}}_{s}\) viene dada por

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=\left(\left(m R^{2} \omega_{z}\right)^{2}+\left(h m R \omega_{z}\right)^{2}\right)^{1 / 2}=m R \omega_{z}\left(h^{2}+R^{2}\right)^{1 / 2} \nonumber \]

La dirección de la\(\overrightarrow{\mathbf{L}}_{S}\) viene dada por (Figura 19.7)

\[-\frac{L_{S, z}}{L_{S, r}}=\frac{R}{h}=\tan \phi \nonumber \]

También presentamos un argumento geométrico. Supongamos que la partícula tiene coordenadas (x, y, h). El momento angular sobre el origen viene dado por\(\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{r}}_{S} \times \overrightarrow{\mathbf{p}}\). Los vectores\(\overrightarrow{\mathbf{r}}_{S} \text { and } \overrightarrow{\mathbf{p}}\) son perpendiculares entre sí por lo que el momento angular es perpendicular al plano formado por esos dos vectores. Recordemos que la velocidad\(v=R \omega_{z}\). Supongamos que el vector\(\overrightarrow{\mathbf{r}}_{S}\) forma un ángulo\(\phi\) con el eje z. Luego\(\overrightarrow{\mathbf{L}}_{s}\) forma un ángulo\(\phi\) con respecto al plano x − y como se muestra en la figura anterior. La magnitud de\(\overrightarrow{\mathbf{L}}_{S}\) es

\[\left|\overrightarrow{\mathbf{L}}_{s}\right|=\left|\overrightarrow{\mathbf{r}}_{s}\right| m|\overrightarrow{\mathbf{v}}|=\left(h^{2}+R^{2}\right)^{1 / 2} m R \omega_{z} \nonumber \]

La magnitud de\(\overrightarrow{\mathbf{L}}_{s}\) es constante, pero su dirección está cambiando a medida que la partícula se mueve en órbita circular alrededor del eje z, barriendo un cono como se muestra en la Figura 19.8. Dibujamos el vector\(\overrightarrow{\mathbf{L}}_{S}\) en el origen porque está definido en ese punto.

Figura 19.8 La dirección del momento angular alrededor del punto\(S\) barre un cono

El punto importante a tener en cuenta respecto a este cálculo es que para cualquier punto a lo largo del eje z no en el centro de la órbita circular de una sola partícula, el momento angular alrededor de ese punto no apunta a lo largo del eje z sino que tiene un componente distinto de cero en el plano x − y (o en el\(-\hat{\mathbf{r}}\) dirección si usa coordenadas polares). El componente z del momento angular alrededor de cualquier punto a lo largo del eje z es independiente de la ubicación de ese punto a lo largo del eje.