25.6: Leyes de Kepler
- Page ID
- 124990
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ley de Órbita Elíptica
I. Cada planeta se mueve en una elipse con el sol en un foco.
Cuando la energía es negativa,\(E<0\), y de acuerdo con la Ecuación (25.3.14),
\[\varepsilon=\left(1+\frac{2 E L^{2}}{\mu\left(G m_{1} m_{2}\right)^{2}}\right)^{\frac{1}{2}} \nonumber \]
y la excentricidad debe estar dentro del rango\(0 \leq \varepsilon<1\). Estas órbitas son círculos o elipses. Tenga en cuenta que la ley de órbita elíptica solo es válida si asumimos que solo hay una fuerza central actuando. Estamos ignorando las interacciones gravitacionales debidas a todos los demás cuerpos del universo, una aproximación necesaria para nuestra solución analítica.
Ley de Igualdad de Área
II. El vector de radio desde el sol hasta un planeta barre áreas iguales en el mismo tiempo.
Usando geometría analítica en el límite de Δθ pequeña, la suma de las áreas de los triángulos en la Figura 25.9 viene dada por
\[\Delta A=\frac{1}{2}(r \Delta \theta) r+\frac{(r \Delta \theta)}{2} \Delta r \nonumber \]
La tasa promedio del cambio de área\(\Delta A\), en el tiempo,\(\Delta t\), viene dada por
\[\Delta A=\frac{1}{2} \frac{(r \Delta \theta) r}{\Delta t}+\frac{(r \Delta \theta)}{2} \frac{\Delta r}{\Delta t} \nonumber \]
En el límite como\(\Delta t \rightarrow 0, \Delta \theta \rightarrow 0\), esto se convierte
\[\frac{d A}{d t}=\frac{1}{2} r^{2} \frac{d \theta}{d t} \label{25.5.4} \]
Recordemos que según la Ecuación (25.3.7) (reproducida a continuación como Ecuación\ ref {25.5.5}), el momento angular está relacionado con la velocidad angular\(d \theta / d t\) por
\[\frac{d \theta}{d t}=\frac{L}{\mu r^{2}} \label{25.5.5} \]
y Ecuación\ ref {25.5.4} es entonces
\[\frac{d A}{d t}=\frac{L}{2 \mu} \label{25.5.6} \]
Porque\(L\) y\(\mu\) son constantes, la tasa de cambio de área con respecto al tiempo es una constante. Esto suele ser referido familiarmente por la expresión: áreas iguales son barridas en tiempos iguales (ver Leyes de Kepler al comienzo de este capítulo).
Ley de Periodo
III. El periodo de revolución T de un planeta alrededor del sol está relacionado con el semieje mayor a de la elipse por\(T^{2}=k a^{3}\) donde k es el mismo para todos los planetas.
Cuando Kepler declaró su ley de época para órbitas planetarias basadas en la observación, solo notó la dependencia de la mayor masa del sol. Debido a que la masa del sol es mucho mayor que la masa de los planetas, su observación es una excelente aproximación.
Para demostrar la tercera ley comenzamos reescribiendo la Ecuación\ ref {25.5.6} en la forma
\[2 \mu \frac{d A}{d t}=L \label{25.5.7} \]
La ecuación\ ref {25.5.7} se puede integrar como
\[\int_{\text {orbit }} 2 \mu d A=\int_{0}^{T} L d t \nonumber \]
donde\(T\) está el periodo de la órbita. Para una elipse,
\[\int_{\text {orbit }}d A=\pi ab \nonumber \]
donde\(a\) está el semieje mayor y\(b\) es el semieje menor (Figura 25.10).
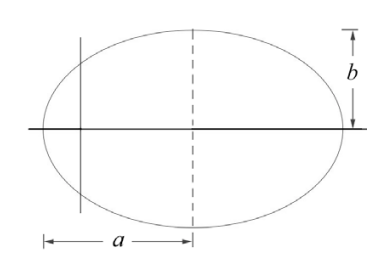
Así tenemos
\[T=\frac{2 \mu \pi a b}{L} \label{25.5.10} \]
Ecuación al cuadrado\ ref {25.5.10} luego rinde
\[T^{2}=\frac{4 \pi^{2} \mu^{2} a^{2} b^{2}}{L^{2}} \nonumber \]
En el Apéndice 25B, la Ecuación (25.B.20) da el momento angular en términos del eje semimajuor y la excentricidad. La sustitución del momento angular en la Ecuación (25.5.11) rinde
\[T^{2}=\frac{4 \pi^{2} \mu^{2} a^{2} b^{2}}{\mu G m_{1} m_{2} a\left(1-\varepsilon^{2}\right)} \nonumber \]
En el Apéndice 25B, la Ecuación (25.B.17) da el semieje menor que tras la sustitución en la Ecuación (25.5.12) produce
\[T^{2}=\frac{4 \pi^{2} \mu^{2} a^{3}}{\mu G m_{1} m_{2}} \nonumber \]
Usando la Ecuación (25.2.1) para la masa reducida, el cuadrado del período de la órbita es proporcional al semieje mayor al cubo,
\[T^{2}=\frac{4 \pi^{2} a^{3}}{G\left(m_{1}+m_{2}\right)} \nonumber \]