27.4: Ley de Pascal - Presión en función de la profundidad en un fluido de densidad uniforme en un campo gravitacional uniforme

Considera un fluido estático de densidad uniforme\(rho\). Elija un sistema de coordenadas tal que el eje z apunte verticalmente hacia abajo y el plano z = 0 esté en la superficie del fluido. Elija un elemento de volumen cilíndrico infinitesimal del fluido a una profundidad z, área de sección transversal A y espesor dz como se muestra en la Figura 27.3. El volumen del elemento es\(d V=A d z\) y la masa del fluido contenido dentro del elemento es\(d m=\rho A d z\).

Figura 27.2: Sistema de coordenadas para fluido

La superficie del elemento cilíndrico fluido infinitesimal tiene tres caras, dos tapas y el cuerpo cilíndrico. Debido a que el fluido es estático, la fuerza debida a la presión del fluido apunta hacia adentro en cada una de estas tres caras. Las fuerzas sobre la superficie cilíndrica se suman a cero. En la tapa de extremo en z, la fuerza debida a la presión del fluido por encima de la tapa final es hacia abajo,\(\overrightarrow{\mathbf{F}}(z)=F(z) \hat{\mathbf{k}}\) donde F (z) es la magnitud de la fuerza. En la tapa final a z + dz, la fuerza debida a la presión del fluido por debajo de la tapa final es hacia arriba,\(\overrightarrow{\mathbf{F}}(z+d z)=-F(z+d z) \hat{\mathbf{k}}\) donde\(F(z+d z)\) está la magnitud de la fuerza. La fuerza gravitacional que actúa sobre el elemento viene dada por\(\overrightarrow{\mathbf{F}}^{g}=(d m) g \hat{\mathbf{k}}=(\rho d V) g \hat{\mathbf{k}}=\rho A d z g \hat{\mathbf{k}}\). También hay fuerzas radiales hacia adentro en el cuerpo cilíndrico que suman a cero. El diagrama de fuerza corporal libre sobre el elemento se muestra en la Figura 27.3.

Figura 27.3: Diagrama de fuerza de cuerpo libre sobre elemento fluido cilíndrico

La suma vectorial de las fuerzas es cero porque el fluido es estático (Segunda Ley de Newton). Por lo tanto en el\(+\hat{\mathbf{k}}\)\[F(z)-F(z+d z)+\rho A d z g=0 \nonumber \] resultado conocido como Ley de Pascal.

Ejemplo 27.1 Presión en el Océano de la Tierra

¿Cuál es el cambio en la presión entre una profundidad de 4 km y la superficie en el océano terrestre?

Solución

Comenzamos asumiendo que la densidad del agua es uniforme en el océano, y así podemos usar la Ley de Pascal, Eq. (27.4.7) para determinar la presión, donde usamos\(\rho=1.03 \times 10^{3} \mathrm{kg} \cdot \mathrm{m}^{-3}\) para la densidad del agua de mar (Cuadro 27.1). Entonces\ [\ begin {array} {l}
P (z) -P (z=0) =\ rho g z\\
=\ izquierda (1.03\ veces 10^ {3}\ mathrm {kg}\ cdot\ mathrm {m} ^ {-3}\ derecha)\ izquierda (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ derecha)\ izquierda (4\ veces 10^ {3}\ mathrm {m}\ derecha)\\
=40\ veces 10^ {6}\ mathrm {Pa}
\ end {array}\ nonumber\]

Ejemplo 27.2 Presión en una muestra giratoria en una centrífuga

En una ultra centrífuga, se hace girar una cámara llena de líquido con una alta velocidad angular ω alrededor de un eje fijo. La densidad ρ del fluido es uniforme. El lado abierto de la cámara está a una\(r_{o}\) distancia del eje fijo. La cámara tiene área de sección transversal A y de longitud L, (Figura 27.4).

Figura 27.4: Representación esquemática de centrífuga

La cámara está girando lo suficientemente rápido como para ignorar el efecto de la gravedad. Determinar la presión en el fluido en función de la distancia r del eje fijo.

Solución

Elija coordenadas polares en el plano de movimiento circular. Considere un elemento de pequeño volumen del fluido de área transversal A, espesor dr, y masa\(d M=\rho A d r\) que se ubica a una distancia r del eje fijo. Denote la presión en un extremo del elemento de volumen por\(P(r)=F(r) / A\) y la presión en el otro extremo por\(P(r+d r)=F(r+d r) / A\). El diagrama de fuerza de cuerpo libre en el elemento de fluido volumétrico se muestra en la Figura 27.5.

Figura 27.5: Diagrama de fuerza de cuerpo libre que muestra solo las fuerzas radiales sobre el elemento fluido en la centrífuga

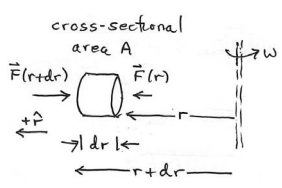
El elemento se está acelerando hacia adentro con componente radial de la aceleración,\(a_{r}=-r \omega^{2}\). La Segunda Ley de Newton aplicada al elemento fluido es entonces\[(P(r)-P(r+d r)) A=-(\rho A d r) r \omega^{2} \nonumber \] Podemos reescribir la Eq. (27.4.9) como\[\frac{P(r+d r)-P(r)}{d r}=\rho r \omega^{2} \nonumber \] y tomar el límite dr → 0 resultando en\[\frac{d P}{d r}=\rho r \omega^{2} \nonumber \] Podemos integrar la Eq. (27.4.11) entre una distancia arbitraria r del eje de rotación y el extremo abierto ubicado en\(R_{O}\), donde la presión \(P\left(r_{0}\right)=1 \mathrm{atm}\). \[\int_{P(r)}^{P\left(r_{0}\right)} d P=\rho \omega^{2} \int_{r=r}^{r^{\prime}=r_{0}} r^{\prime} d r^{\prime} \nonumber \]Rendimiento de integración\[P\left(r_{0}\right)-P(r)=\frac{1}{2} \rho \omega^{2}\left(r_{0}^{2}-r^{2}\right) \nonumber \] La presión a una distancia r del eje de rotación es entonces\[P(r)=P\left(r_{0}\right)+\frac{1}{2} \rho \omega^{2}\left(r^{2}-r_{0}^{2}\right) \nonumber \]