5.5: Colisiones Elásticas Oblivas (Miradas), Tratamiento Alternativo

En la Figura V.3, a diferencia de la Figura V.2, la línea horizontal no pretende representar la línea de centros. Más bien, es la dirección de la velocidad inicial de\( m_{1}\), e inicialmente\( m_{2}\) está en reposo. La segunda masa \( m_{2}\)está ligeramente fuera de la línea de la velocidad de\( m_{1}\). Estoy asumiendo que la colisión es elástica, así que eso\( e = 1\). En la parte “antes” de la Figura, he indicado, así como las dos masas, la posición y velocidad\( \bf{V}\) del centro de masa\( C\). La velocidad de\( C\) permanece constante, porque no hay fuerzas externas en el sistema. No he dibujado\( C\) en la parte del “después” de la Figura, porque se pondría un poco en el camino. Piensa en dónde está.

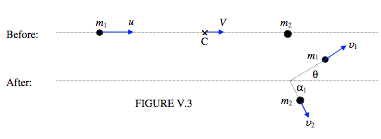
La Figura V.3 muestra la situación en el “espacio de laboratorio”. (Posteriormente, veremos la situación referida a un marco de referencia en el que\( C\) se encuentra en reposo — “centro del espacio de masas”). El ángulo\( \theta\) es el ángulo a través del cual se\( m_{1}\) ha dispersado (el “ángulo de dispersión”). He indicado en la Figura cómo se relaciona con el\( \alpha_{1}\) y\( \beta_{1}\) de la Sección 5.3. Tenga en cuenta que\( m_{2}\) (inicialmente estacionario) se escurre a lo largo de la línea de centros.

Las siguientes dos ecuaciones expresan la constancia del momento lineal del sistema.

\[(m_{1}+m_{2})V = m_{1}u = m_{1}v_{1}\cos\theta + m_{2}v_{2} \cos \alpha_{1}. \tag{5.5.1}\label{eq:5.5.1} \]

Voy a dibujar, en la Figura V.4, la situación “primer plano”, para que se pueda ver más claramente la geometría. Tenga en cuenta que la distancia\( b\) se llama el parámetro de impacto. Es la distancia por la que los dos centros se habrían perdido el uno al otro si no se hubiera dispersado la primera partícula.

En la Figura V.5, dibujo la situación en el espacio del centro de masa, en la que el centro de masa\( C\) es estacionario. En este marco de referencia, sólo tengo que restar\( \bf{V}\) de todas las velocidades. Tenga en cuenta que en el espacio del centro de masa las velocidades de las partículas son inalteradas por la colisión. En el centro del espacio de masa,\( m_{1}\) se dispersa a través de un ángulo\( \theta^{\prime}\), y voy a encontrar una relación entre\( \theta^{\prime}\),\( \theta\) y la relación de masa\( \dfrac{m_{2}}{m_{1}}\).

Comenzaré con la profunda declaración de que

\[\tan \theta = \dfrac{v_{1}\sin\theta}{v_{1}\cos\theta} \tag{5.5.2}\label{eq:5.5.2} \]

Ahora\( v_{1} \sin \theta\) es el\( y\) -componente de la velocidad final de\( m_{1}\) en el espacio de laboratorio. El\( y\) -componente de la velocidad final del espacio\( m_{1}\) en el centro de masa es\( u^{\prime}\sin\theta^{\prime}\), y estos dos son iguales, ya que el\( y\) -componente del movimiento no se ve afectado por el cambio de marco de referencia. Por lo tanto

\[\tan \theta = \dfrac{u'\sin\theta'}{v_{1}\cos\theta}. \tag{5.5.3}\label{eq:5.5.3} \]

Por lo tanto

\[v_{1} \sin \theta = u' \sin \theta'. \tag{5.5.4}\label{eq:5.5.4} \]

Los\( x\) -componentes de las velocidades “antes” y “después” de\( m_{1}\) están relacionados por

\[v_{1} \cos \theta = u' \sin \theta'+ V. \tag{5.5.6}\label{eq:5.5.6} \]

Ecuaciones sustitutas\( \ref{eq:5.5.4}\) y\( \ref{eq:5.5.6}\) en Ecuación\( \ref{eq:5.5.2}\) para obtener

\[\tan \theta = \dfrac{\sin \theta'}{\cos \theta' + V/u'} \tag{5.5.7}\label{eq:5.5.7} \]

Pero

\[(m_{1}+m_{2})V = m_{1}u= m_{1}(u'+V), \tag{5.5.8}\label{eq:5.5.8} \]

a partir de la cual

\[\dfrac{V}{u'} = \dfrac{m_{1}}{m_{2}}. \tag{5.5.9}\label{eq:5.5.9} \]

Al sustituir esto en Ecuación\( \ref{eq:5.5.7}\), obtenemos la relación que buscamos:

\[\tan \theta = \dfrac{\sin \theta '}{cos \theta' +m_{1} /m_{2}}. \tag{5.5.10}\label{eq:5.5.10} \]

Esta relación se ilustra en la Figura V.6 para varias relaciones de masa.

Tratemos de interpretar la Figura. Porque\( m_{2}>m_{1}\), cualquier ángulo de dispersión, hacia adelante o hacia atrás, es posible, pero para\( m_{2}<m_{1}\), la dispersión hacia atrás no es posible, y la dispersión hacia adelante es posible solo hasta un máximo. Esto sólo es de esperar. Así, para un parámetro de impacto de cero o de\( R_{1} + R_{2}\), y\( m_{2}<m_{1}\), el ángulo de dispersión\( \theta\) debe ser cero, y por lo tanto para los parámetros de impacto intermedios debe pasar por un máximo. Esto sería más claro si pudiéramos trazar el ángulo de dispersión versus el parámetro de impacto, y de hecho eso es algo que intentaremos hacer. Mientras tanto es fácil de mostrar, por diferenciación de Ecuación\( \ref{eq:5.5.10}\) (¡hazlo!) , que el ángulo máximo de dispersión es\( \sin^{-1}\mu\), donde

\[ \mu = \dfrac{m_{2}}{m_{1}}. \nonumber \]

Es decir, si la partícula dispersada es muy masiva en comparación con la partícula dispersante, el ángulo de dispersión máximo es pequeño, solo para ser de esperar.

Ahora quiero hacer dos cosas: una, para calcular el ángulo\( \theta\) de dispersión en función del parámetro de impacto, y dos, calcular\( \dfrac{v_{1}}{u}\) en función del ángulo de dispersión. Voy a comenzar con las Ecuaciones 5.4.1, 5.4.2 y 5.4.4, a excepción de las siguientes. Asumiré\( e = 1\) (colisión elástica), y\( u_{2}=0\) (\( m_{2}\)es inicialmente estacionaria), y\( \beta_{2}=0\) (dado que inicialmente\( m_{2}\) es estacionaria, debe moverse a lo largo de la línea de centros después de la colisión). Como quiero intentar calcular el ángulo de dispersión, voy a escribir\( \theta + \alpha_{1}\) para\( \beta_{1}\) (ver Figura V.4). También voy a escribir\( r_{1}\),\( r_{2}\) y\( \mu\) para las relaciones adimensionales\( \dfrac{v_{1}}{u}\),\( \dfrac{v_{2}}{u}\) y\( \dfrac{m_{2}}{m_{1}}\) respectivamente. Con esos pequeños cambios, las ecuaciones 5.4.1, 5.4.2 y 5.4.4 se convierten

\[r_{1}\cos(\theta + \alpha_{1}) + \mu r_{2} = \cos \alpha_{1}, \tag{5.5.11}\label{eq:5.5.11} \]

\[r_{1}sin(\theta + \alpha_{1})= \sin \alpha_{1}, \tag{5.5.12}\label{eq:5.5.12} \]

\[r_{2} - r_{1}\cos(\theta + \alpha_{1})= \cos \alpha_{1}. \tag{5.5.13}\label{eq:5.5.13} \]

Eliminar\( r_{2}\) de Ecuaciones\( \ref{eq:5.5.11}\) y\( \ref{eq:5.5.13}\) obtener

\[r_{1}\cos(\theta + \alpha_{1})=M \cos \alpha_{1}, \tag{5.5.14}\label{eq:5.5.14} \]

donde

\[M = \dfrac{1- \mu}{1+ \mu} = \dfrac{m_{1}-m_{2}}{m_{1}+m_{2}}. \tag{5.5.15}\label{eq:5.5.15} \]

Si ahora eliminamos\( \alpha_{1}\) de Ecuaciones\( \ref{eq:5.5.12}\) y\( \ref{eq:5.5.14}\), obtenemos la relación entre\( \dfrac{v_{1}}{u}\) y el ángulo de dispersión, que fue el segundo de nuestros dos objetivos anteriores. La eliminación se realiza fácilmente de la siguiente manera. Expandir\ sin y cos de\( \theta + \alpha_{1}\) en las dos ecuaciones, dividir ambos lados de cada ecuación por\( \cos \alpha_{1}\) y eliminar\( \tan\alpha_{1}\) entre las dos ecuaciones. El resultado es

\[r^{2}_{1} (1+M)\cos\theta +M = 0. \tag{5.5.16}\label{eq:5.5.16} \]

Vamos a echar un vistazo a esta ecuación en un momento, pero mientras tanto, en lugar de eliminar\( \alpha_{1}\) de Ecuaciones\( \ref{eq:5.5.12}\) y\( \ref{eq:5.5.14}\), vamos a eliminar\( r_{1}\). Esto nos dará una relación entre el ángulo de dispersión\( \theta\) y\( \alpha_{1}\), y, dado que\( \alpha_{1}\) es estrecha relación con el parámetro de impacto (ver Figura V.4) esto logrará el primero de nuestros objetivos, es decir, encontrar el ángulo de dispersión en función del parámetro de impacto. Si haces el álgebra, deberías encontrar que la relación entre\( \theta\) y\( \alpha_{1}\) es

\[t = \dfrac{a(1-M)}{a^{2}+M}, \tag{5.5.17}\label{eq:5.5.17} \]

donde

\[t = \\tan \theta \quad and \quad a = \\tan \alpha_{1}. \tag{5.5.17a,b}\label{eq:5.5.17a,b} \]

Ahora vamos

\[b' = \dfrac{b}{R_{1}+R_{2}} \tag{5.5.18}\label{eq:5.5.18} \]

y de la Figura V.5 vemos que

\[b' = \sin \alpha_{1}. \tag{5.5.19}\label{eq:5.5.19} \]

Al eliminar\( \alpha_{1}\) de Ecuaciones\( \ref{eq:5.5.17}\) y\( \ref{eq:5.5.19}\), obtenemos la relación requerida entre el ángulo de dispersión\( \theta\) y el parámetro de impacto (adimensional)\( b'\):

\[\tan \theta = \dfrac{s\mu b' \sqrt{1-b^{t^{2}}}}{1- \mu + 2 \mu b^{t^{2}}}. \tag{5.5.20}\label{eq:5.5.20} \]

Esta relación se muestra en la Figura V .7. Los valores de la relación de masa\( \mu\) (\(=frac{m_{2}}{m_{1}}\)) son (del

más bajo hacia arriba)\( \dfrac{1}{8} , \dfrac{1}{4}, \dfrac{1}{2}, \dfrac{9}{10}, 1 , \dfrac{10}{9}, 2, 4, 8\) y (discontinuo)\( \infty\). Esta Figura es quizás un poco más fácil de interpretar que la Figura V.6. Se puede ver que para\( \mu > 1\), cualquier ángulo de dispersión es posible, pero para\( \mu < 1\), el ángulo de dispersión tiene un valor máximo posible, inferior a 90 °, y el ángulo de dispersión es cero para\( b'\) = 0 o 1.

Ejercicio\(\PageIndex{1}\)

Vimos, por diferenciación de Ecuación\( \ref{eq:5.5.10}\), que el ángulo máximo de dispersión era\( \sin^{-1}\mu\). Ahora muestran lo mismo por diferenciación de Ecuación\( \ref{eq:5.5.20}\). (Esto no es tan fácil, ¿verdad?)

Mostrar que el ángulo de dispersión es mayor para un parámetro de impacto de

\[b' = \sqrt{\dfrac{1 - \mu}{2}}. \tag{5.5.21}\label{eq:5.5.21} \]

Solución

Notarás que, para/(b' = 0/) (colisión frontal) el ángulo de dispersión cambia abruptamente de 0 a 180 ° a medida que la relación de masa cambia de menos de 1 a más de 1. No hay problema ahí. Pero si la relación de masa es exactamente 1 (no el bit más pequeño menos ni el más pequeño más) el ángulo de dispersión es aparentemente de 90 °. Esto puede provocar cierto desconcierto hasta que se dé cuenta de que para una colisión frontal con\( \mu = 1\) la primera esfera llega a un alto muerto.

El caso de\( mu = \infty\) (segunda esfera inamovible) es de cierto interés. Es fácil en ese caso calcular cómo varía el ángulo de dispersión con el parámetro de impacto para una colisión elástica, simplemente requiriendo que la esfera dispersa obedezca la ley de reflexión, y sin ninguna referencia a la Ecuación\( \ref{eq:5.5.20}\).

Ejercicio\(\PageIndex{2}\)

Ejercicio fácil.

Sin ninguna referencia a la Ecuación\( \ref{eq:5.5.20}\), mostrar que, si la segunda bola es inamovible, el ángulo de dispersión está relacionado con el parámetro de impacto por

\[\theta = 180° - 2sin^{-1} b'. \tag{5.5.22}\label{eq:5.5.22} \]

Ejercicio no tan fácil. Demostrar que, en el límite como\( \mu\rightarrow\infty\), Ecuación\( \ref{eq:5.5.20}\) se acerca a Ecuación\( \ref{eq:5.5.22}\).

En cualquier caso, el caso limitante a medida que la segunda esfera se vuelve inamovible se muestra como una curva discontinua en la Figura V.7.

Ejercicio de Dificultad Intermedia. La relación de masa\( \dfrac{m_{2}}{m_{1}}\) es 0.9, y el ángulo de dispersión es 50\(^{\circ}\). ¿Cuál fue el parámetro de impacto?

RESPUESTAS

b' = 0.07270 o 0.58540.

Ahora hemos tratado la dirección del movimiento de\( m_{1}\) después de la dispersión como una función del parámetro de impacto. Ahora debemos mirar la velocidad de\( m_{1}\) después de la colisión, y esto nos lleva de vuelta a la Ecuación\( \ref{eq:5.5.16}\), que da es la velocidad (\( r_{1}=\dfrac{v_{1}}{u}\)) en función del ángulo de dispersión\( \theta\). Es de 11 pulgadas cuadráticas\( r_{1}\), por lo que, para un ángulo de dispersión dado hay dos velocidades posibles —lo cual no es sorprendente, porque un ángulo de dispersión dado puede surgir de dos parámetros de impacto diferentes, como acabamos de enterarnos. Podemos mostrar convenientemente la relación entre\( r_{1}\) y\( \theta\) simplemente trazando la ecuación en coordenadas polares. Voy a volver a escribir la ecuación aquí para una fácil referencia:

\[r^{2}_{1} = r_{1}(1+M)\cos\theta + M = 0. \tag{5.5.16.}\label{eq:5.5.16.} \]

Aquí,\( M = \dfrac{1-\mu}{1+ \mu }=\dfrac{1}{1+ \mu } \), pero quiero escribir la ecuación en términos de las fracciones de masa

\[q_{1} = \dfrac{m_{1}}{m_{1}+m_{2}} = \dfrac{1}{1 + \mu} \quad and \quad q_{2} = \dfrac{m_{2}}{m_{1}+m_{2}}=\dfrac{\mu}{1 + \mu}. \tag{5.5.23a,b}\label{eq:5.5.23a,b} \]

Si trabajas en esto por un corto tiempo, encontrarás que la ecuación\( \ref{eq:5.5.16}\) se convierte en

\[r_{1}^{2} +q_{1}^{2} -2r_{1}q_{1}\cos\theta = q_{2}^{2}. \tag{5.5.24}\label{eq:5.5.24} \]

y luego uno es superado con un deseo abrumador de dibujar un triángulo:

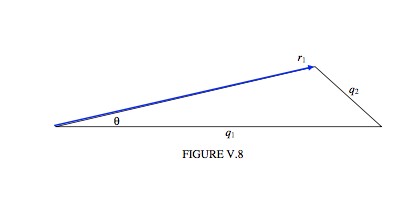
Para una proporción de masa dada, el lugar de\( r_{1}\) (la velocidad) versus\( \theta\) (el ángulo de dispersión) es tal que\( q_{1}\) y\( q_{2}\) son constantes, en otras palabras, es un círculo:

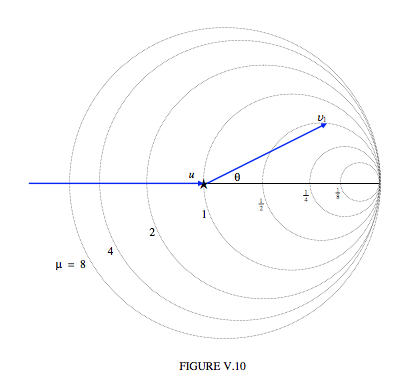
Se puede imaginar que la primera partícula entra por la izquierda a la velocidad u y la colisión tiene lugar en el asterisco, y, después de la colisión, se mueve a una velocidad\( r_{1}\) veces\( u\) en una dirección\( \theta\), estando determinada la magnitud de su vector de velocidad por donde el vector se cruza con el círculo (en dos posibles lugares) dado por Ecuación\( \ref{eq:5.5.24}\). El ángulo máximo de dispersión corresponde a un vector de velocidad que es tangente al círculo. Si el asterisco es el polo (origen) de las coordenadas polares, el centro del círculo está a una\( q_{1}\) distancia del polo, y su radio es\( q_{2}\). La Figura V.10 muestra los círculos correspondientes a varias relaciones de masa. La Figura ilustra gráficamente la relación entre\( u\),\( v_{1}\),\( \theta\) y\( \mu\). Se puede ver, por ejemplo, que si\( \mu>1\), la dispersión a través de cualquier ángulo es posible, y la relación entre\( v_{1}\) y\( \theta\) es única; pero si\( \mu<1\), solo es posible la dispersión hacia adelante, hasta un máximo\( \theta\), y, para un dado\( \theta\), hay dos soluciones para \( v_{1}\).

Esto trata de lo que le sucede a la esfera\( m_{1}\). Ahora podemos dirigir nuestra atención\( m_{2}\). Partiendo de Ecuaciones\( \ref{eq:5.5.11}\)\( \ref{eq:5.5.13}\),\( \ref{eq:5.5.12}\) y, vamos a querer eliminar\( r_{1}\) y\( \theta\) -de hecho cualquier cosa que pertenezca a la esfera\( m_{1}\).

Si se refiere a la Figura V.4 verá que, después de la colisión,\( m_{2}\) se escurre en ángulo\( \alpha_{1}\) con la dirección original del movimiento de\( m_{1}\). Por lo tanto creo que es de interés encontrar una relación entre \( r_{2}\)(\ dfrac {v_ {2}} {u}) y\( \alpha_{1}\). Si logramos hacer esto, significa que también podemos encontrar una relación, si la queremos, entre\( r_{2}\) y el parámetro de impacto, ya que\( b' = \sin\alpha_{1}\). Es fácil\( r_{1}\) de eliminar de las ecuaciones\( \ref{eq:5.5.12}\) y\(\ref{eq:5.5.13}\), y luego se puede obtener\( \tan(\theta + \alpha_{1})\) de la ecuación\( \ref{eq:5.5.14}\), y de ahí obtener la relación requerida:

\[r_{2} = \dfrac{2\cos\alpha_{1}}{1 + \mu}. \tag{5.5.25}\label{eq:5.5.25} \]

Dibujaré esta relación como una gráfica polar, \( r_{2}\)versus\( \alpha_{1}\), en la Figura V.11. Dejaré al lector para que haga ejercicio y dibuje la relación entre\( r_{2}\) y\( b'\) si él o ella lo desea. La ecuación V.11 es la ecuación polar a un círculo de radio\( \dfrac{1}{1+\mu}\).

Ejemplo\(\PageIndex{1}\)

Supongamos que la relación de masa\( \mu=\dfrac{m_{2}}{m_{1}} = 0.5\) y el ángulo de dispersión es de\( \theta=\) 20 °. La ecuación\( \ref{eq:5.5.16}\) o Figura V.10 mostrará que\( r_{1}\) = 0.8696 o 0.3833. La ecuación\( \ref{eq:5.5.17}\) mostrará que\( \alpha_{1}\) = 58 ° .4 o 11 ° .6. Y la Ecuación\( \ref{eq:5.5.25}\) o Figura V.11 mostrará eso\( r_{2}\) = 0.6983 o 1.306. Dejaré al lector determinar qué valores alternativos de\( r_{1}\),\( r_{2}\) e\( \alpha_{1}\) ir juntos.