19.10: Ejemplos de Movimiento Cicloidal en Física

Me vienen a la mente varios ejemplos de movimiento cicloidal en la física. Una es la nutación de un top, que se describe en la Sección 4.10 del Capítulo 10. El eje de la Tierra nuta de manera similar. Otro ejemplo bien conocido es el movimiento de un electrón en campos eléctricos y magnéticos cruzados. Esto se describe en el Capítulo 8 de la sección Electricidad y Magnetismo de estas notas. En cosmología, si la densidad media del Universo es baja, el Universo se expande indefinidamente, pero, si la densidad es mayor que una cierta densidad crítica, el factor de escala (adimensional)\(R\) del Universo se expande y contrae con el tiempo t de acuerdo con las siguientes ecuaciones cicloidales paramétricas:

\[ R = \dfrac{\Omega_0}{2(\Omega_0 -1) }(1 - \cos 2 \theta ) , \label{19.10.1}\tag{19.10.1} \]

\[ t = \dfrac{\Omega_0}{2(\Omega_0 -1)^{3/2} }(2 \theta - \sin 2 \theta ). \label{19.10.2}\tag{19.10.2} \]

Aquí\(t\) se expresa en unidades del recíproco de la presente constante Hubble, y\( \Omega_0\) es la relación de la densidad presente del Universo a la densidad requerida para “cerrar” el Universo.

Un ejemplo menos conocido se refiere a la propagación del sonido en la atmósfera. En la troposfera, que es la parte inferior de la atmósfera hasta unos 11 km, la temperatura disminuye aproximadamente linealmente con la altura. En ese caso el sonido viaja a través de la troposfera en un camino cicloidal. La velocidad del sonido en un gas es proporcional a la raíz cuadrada de la temperatura. (Si te estás preguntando cómo depende de la presión P y la densidad\( \rho \), la respuesta es que depende de la relación P/\( \rho \) - y esta relación es proporcional a la temperatura.) En cualquier caso, si la temperatura disminuye linealmente con la altura, la velocidad del sonido\(v\) varía con la altura\(y\) como

\[ v = v_0 \sqrt{1 - cy} \label{19.10.3}\tag{19.10.3} \]

donde c es una constante, igual a aproximadamente 0.023 km ⁻¹ .Ahora para trazar un rayo de sonido a través de la atmósfera, tenemos que entender cómo cambia la dirección de propagación a medida que el sonido pasa a través de capas de aire de diferente temperatura. Esto se rige, como con la luz, por la ley de Snell (ver figura XIX.11):

\[ \dfrac{dv}{v} = - \tan \psi d \psi \label{19.10.4}\tag{19.10.4} \]

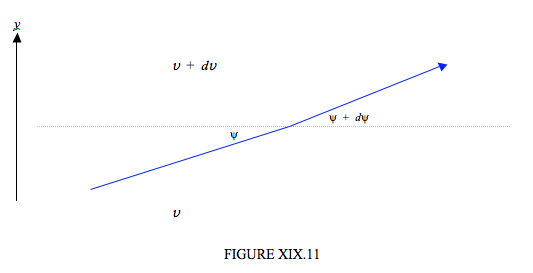
La ley de Snell establece que cuando el sonido (o la luz) entra en un medio más lento (es decir, uno en el que la velocidad de propagación es más lenta) se dobla hacia lo normal. He dibujado la figura XIX.11 para representar la situación en la troposfera donde la temperatura (y de ahí la velocidad del sonido\( v \)) disminuye con la altura. Es decir,\(dv/dy \) es negativo. En otras palabras,\(dv\) en la figura XIX es negativo, y la Ecuación\( \ref{19.10.4} \) indica que\( d\psi \) es positivo, tal como se dibuja. En caso de que no reconozcas esta forma diferencial de la ley de Snell, intenta integrarla desde\(v_1\)\(v_2\) y\(\psi_1\) hacia\(\psi_2 \), y debería asumir su forma integral más familiar. Si ahora eliminas\(v\) entre Ecuaciones\( \ref{19.10.3} \) y\(\ref{19.10.4}\), obtendrás una relación diferencial entre\(y\) y\( \psi \), que, al integrarse, se convierte en

\[ cy = 1 - \dfrac{\cos^2 \psi}{\cos^2 \psi_0} \label{19.10.5}\tag{19.10.5} \]

donde\( \psi_ 0\) está el valor a nivel del suelo de\( \psi \). Si introducimos

\[ a = \dfrac{1}{2c \cos ^2 \psi_0} , \label{19.10.6}\tag{19.10.6} \]

ecuación\( \ref{19.10.5} \) se puede reescribir convenientemente

\[ y = 2a(\sin^2 \psi - s\in^2 \psi_0) = 2a( \cos^2 \psi_0 - \cos^2 \psi \label{19.10.7}\tag{19.10.7} \]

Ahora\(\tan \psi = dy/dx\), y la eliminación de\(y\) entre esto y Ecuación\( \ref{19.10.7} \) dará una relación diferencial entre\(x\) y\( \psi \), que, al integrarse, se convierte en

\[ x = a[2(\psi - \psi_ 0 ) + \sin 2 \psi - \sin 2 \psi_0 ]. \label{19.10.8}\tag{19.10.8} \]

Las ecuaciones\( \ref{19.10.7} \) y\( \ref{19.10.8} \) son las ecuaciones paramétricas de la trayectoria sonora a través de la troposfera, y describen un cicloide.

Ejercicio\(\PageIndex{1}\): Problem for a Rainy Day

Si\(x\) = 2.0 y\(y\) = 1.6, ¿qué son\( \psi\) y\( \psi_0\)?

Solución

Yo lo hago\( \psi = 69 ^\circ, \psi_0 = 15 ^\circ 52'\).