20.3: Módulo de cizallamiento y constante de torsión

Imagínese que tenemos un bloque rectangular de material sólido, como se muestra en el lado izquierdo de la Figura XX.6. Ahora aplicamos un par de fuerzas tangenciales\(F\) como se muestra en el lado derecho. (No he decidido ir del todo hablador e informal diciendo “un par” de fuerzas; lejos de eso — estoy usando la palabra “pareja” en su sentido formal en mecánica.) El material sufrirá una deformación angular, y la relación de la fuerza tangencial por unidad de área a la deformación angular resultante se denomina módulo de cizallamiento o módulo de rigidez. Su unidad SI es N m ⁻² rad ⁻¹ y sus dimensiones son ML ⁻¹ T ⁻² θ ⁻¹. (Yo aconsejaría no usar “pascales” por radián. La unidad “pascal” se restringe mejor a la presión, que es la fuerza normal por unidad de área, y no es lo mismo que la fuerza tangencial por unidad de área que estamos discutiendo aquí.) Debes convencerte de que la definición debe especificar la fuerza F, no el par proporcionado por la pareja. Si el bloque fuera el doble de grueso, y las fuerzas fueran las mismas, seguirías obteniendo la misma deformación angular.

Si mantiene fijo un extremo de un alambre o varilla y aplica un par al otro extremo, este extremo se torcerá a través de un ángulo, y la relación entre el par aplicado y el ángulo a través del cual se tuerce el cable es la constante de torsión\(c\),, del cable. Se puede ver como la constante de torsión depende del módulo\( \eta \) de cizallamiento del metal y del radio\(a\) y longitud\(l\) del alambre por el método de dimensiones. Puedes empezar suponiendo que

\[ c \propto \eta^\alpha a^\beta l^\gamma, \nonumber \]

pero pronto te encontrarás en dificultad porque\(a\) y\(l\) son cada uno de dimensión L. Sin embargo, probablemente no tendrás dificultad en hacer la suposición de que\( \gamma = −1\) (cuanto más largo sea el cable, más fácil es torcerse), y el análisis dimensional pronto lo demostrará\( \alpha = 1 \) y \(\beta = 4 \)- lo cual, al ser interpretado, significa que es mucho más difícil torcer un alambre grueso que un alambre delgado. Pero, ¿podemos hacerlo mejor y obtener una expresión que no sea una mera proporcionalidad para la constante de torsión? ¿Podemos encontrar la constante de proporcionalidad? Probemos primero algunos problemas más simples, y veamos cómo van las cosas.

Consideremos una tira larga y delgada o cinta de metal. Por largo y delgado quiero decir que su longitud es mucho mayor que su ancho, y su ancho es mucho mayor que su grosor. Puedo usar cualquier símbolo que me guste para representar cualquier cantidad que me guste, así podría, si lo deseara, usar\( \Xi \) para el largo,\(m_\alpha \) para el ancho, y\(G_2\) para el grosor. En cambio, los símbolos que elegiré para representar el largo, ancho y grosor de la tira van a ser, respectivamente,\( l, 2 \pi r \) y\( \delta r\). Esto parece tonto por el momento, pero al final te alegrarás de haber hecho esta elección. La tira se muestra en el lado izquierdo de la Figura XX.7.

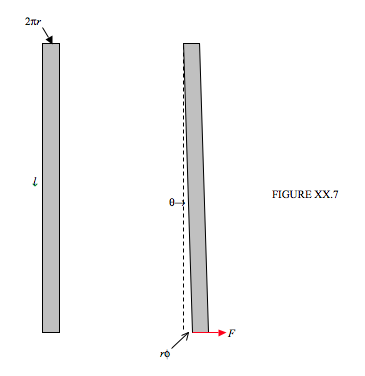
Ahora voy a fijar el extremo superior de la tira y aplicar una fuerza\(F\) al extremo inferior, como se muestra en el lado derecho de la Figura XX.7, y puedo usar cualquier símbolo que me guste para representar el desplazamiento del extremo inferior, y elijo el símbolo\( r \phi \). Esto significa que el desplazamiento angular\( \theta \) es igual a\( r \phi / l \) .La fuerza tangencial por unidad de área es\(F/(2 \pi r \delta r)\), y por lo tanto

\[ \eta = \frac{Fl}{2 \pi \phi r^2 \delta r} , \tag{20.3.1}\label{eq:20.3.1} \]

o

\[ F = \frac{2 \pi \eta \phi r^2 \delta r}{l}. \tag{20.3.2}\label{eq:20.3.2} \]

Ahora voy a restaurar la tira a su forma original, y luego la voy a enrollar en un tubo cilíndrico hueco, para que ahora parezca una pajita metálica para beber. La circunferencia de la paja es\(2 \pi r\), su radio es\(r\) y su grosor es\(\delta r\) (Figura XX.8). (¡Ahora mi notación empieza a tener sentido!)

Sostendré fijo el extremo superior del tubo y aplicaré un par\( \tau = Fr\) al extremo inferior. Evidentemente, el tubo se torcerá a través de un ángulo azimutal\( \phi \) dado por

\[ \tau = \frac{ 2 \pi \eta ^3 \delta r }{l} \phi . \tag{20.3.3}\label{eq:20.3.3} \]

Por lo tanto, la constante de torsión del tubo hueco es

\[ c = \frac{2 \pi \eta r^3 \delta r }{l}. \tag{20.3.4}\label{eq:20.3.4} \]

La constante de torsión de un cilindro sólido largo (un cable) de radio a es la integral de esto de 0 a\(a \), que es

\[ c = \frac{\pi \eta a^4 }{2l} \tag{20.3.5}\label{eq:20.3.5} \]