2.1: Ecuación de Lagrange

En muchos casos, las restricciones impuestas al movimiento 3D de un sistema de\(N\) partículas pueden describirse mediante ecuaciones algebraicas\(N\) vectoriales (es decir,\(3 N\) escalares)\[\mathbf{r}_{k}=\mathbf{r}_{k}\left(q_{1}, q_{2}, \ldots, q_{j}, \ldots, q_{J}, t\right), \quad \text { with } 1 \leq k \leq N,\] donde\(q_{j}\) hay ciertas coordenadas generalizadas que (junto con las restricciones) definen completamente la posición del sistema . Su número\(J \leq 3 N\) se llama el número de los grados reales de libertad del sistema. Las restricciones que permiten tal descripción se denominan holonómicas. \({ }^{1}\)

Por ejemplo, para el problema discutido brevemente en la Sección 1.5, a saber, el talón que se desliza a lo largo de un anillo giratorio (Figura 1)\(J=1\), porque con las restricciones impuestas por el anillo, la posición de la perla está determinada de manera única por una sola coordenada generalizada, por ejemplo, su ángulo polar\(\theta\).

Figura 2.1. Una perla en un anillo giratorio como ejemplo de un sistema con solo un grado de libertad\((J=1)\).

En efecto, seleccionando el marco de referencia como se muestra en la Figura 1 y utilizando las fórmulas bien conocidas para las coordenadas esféricas,\({ }^{2}\) vemos que en este caso, la Ec. (1) tiene la forma\[\mathbf{r} \equiv\{x, y, z\}=\{R \sin \theta \cos \varphi, R \sin \theta \sin \varphi, R \cos \theta\}, \quad \text { where } \varphi=\omega t+\text { const },\] con la última constante dependiendo de la selección exacta de los ejes\(x\) y\(y\) y el origen del tiempo. Dado que el ángulo\(\varphi\), en este caso, es una función fija del tiempo, y\(R\) es una constante fija, la posición de la partícula en el espacio en cualquier instante\(t\) está completamente determinada por el valor de su única coordenada generalizada\(\theta\). (¡Tenga en cuenta que su dimensionalidad es diferente a la de las coordenadas cartesianas!)

Volviendo ahora al caso general de los\(J\) grados de libertad, consideremos un conjunto de pequeñas variaciones (llamadas alternativamente “desplazamientos virtuales”)\(\delta q_{j}\) permitidas por las restricciones. Los desplazamientos virtuales difieren de los desplazamientos pequeños reales (descritos por diferenciales\(d q_{j}\) proporcionales a la variación de tiempo\(d t\)) en que no\(\delta q_{j}\) describen el movimiento del sistema como tal, sino su posible variación ver Figura 1.

Figura 2.2. Desplazamiento real\(d q_{j}\) vs. el virtual (es decir, variación)\(\delta q_{j}\).

Generalmente, las operaciones con variaciones son objeto de un campo especial de las matemáticas, el cálculo de las variaciones. \({ }^{3}\)Sin embargo, el único fondo matemático necesario para nuestros propósitos actuales es el entendimiento de que las operaciones con variaciones son similares a las que tienen los diferenciales habituales, aunque necesitamos observar cuidadosamente de qué es función cada variable. Por ejemplo, si consideramos la variación de los vectores de radio (1), en un tiempo fijo\(t\), en función de las variaciones independientes\(\delta q_{j}\), podemos usar la fórmula habitual para la diferenciación de una función de varios argumentos:\({ }^{4}\)\[\delta \mathbf{r}_{k}=\sum_{j} \frac{\partial \mathbf{r}_{k}}{\partial q_{j}} \delta q_{j} .\] Ahora rompamos la fuerza que actúa sobre el \(k^{\text {th }}\)partícula en dos partes: la parte sin fricción, limitante\(\mathbf{N}_{k}\) de la fuerza de reacción y la parte\(\mathbf{F}_{k}\) restante, incluidas las fuerzas de otras fuentes y posiblemente la parte de fricción de la fuerza de reacción. Entonces la ley\(2^{\text {nd }}\) Newton para la\(k^{\text {th }}\) partícula del sistema puede ser reescrita como\[m_{k} \dot{\mathbf{v}}_{k}-\mathbf{F}_{k}=\mathbf{N}_{k} .\] Dado que cualquier variación del movimiento tiene que ser permitida por las restricciones, su vector\(3 N\) -dimensional con componentes\(N\)\(3 \mathrm{D}\) -vector\(\delta \mathbf{r}_{k}\) tiene que ser perpendicular a la \(3 N\)-vector dimensional de las fuerzas de restricción, también con componentes de\(N\) vectores 3D\(\mathbf{N}_{k}\). (Por ejemplo, para el problema mostrado en la Figura 2.1, el vector de desplazamiento virtual\(\delta \mathbf{r}_{k}\) puede dirigirse solo a lo largo del anillo, mientras que la fuerza de restricción\(\mathbf{N}\), ejercida por el anillo, tiene que ser perpendicular a esa dirección). Esta condición puede expresarse como\[\sum_{k} \mathbf{N}_{k} \cdot \delta \mathbf{r}_{k}=0\] donde el producto escalar de vectores\(3 N\) -dimensionales se define exactamente como el de los\(3 \mathrm{D}\) vectores, es decir, como la suma de los productos de los componentes correspondientes de los operandos. La sustitución de la Ec. (4) en la Ec. (5) da como resultado el llamado principio\(D\) 'Alembert:\(^{5}\)\[\sum_{k}\left(m_{k} \dot{\mathbf{v}}_{k}-\mathbf{F}_{k}\right) \cdot \delta \mathbf{r}_{k}=0\] Ahora podemos enchufar la Eq. (3) en la Eq. (6) para llegar\[\sum_{j}\left\{\sum_{k} m_{k} \dot{\mathbf{v}}_{k} \cdot \frac{\partial \mathbf{r}_{k}}{\partial q_{j}}-\mathscr{F}_{j}\right\} \delta q_{j}=0,\] donde los escalares\(\mathscr{J}_{j}\), llamados las fuerzas generalizadas, se definen de la siguiente manera:\({ }^{6}\)

Fuerza generalizada

\[\ \mathscr{F}_{j} \equiv \sum_{k} \mathbf{F}_{k} \cdot \frac{\partial \mathbf{r}_{k}}{\partial q_{j}}.\]

Ahora podemos usar el argumento estándar del cálculo de variaciones: para que el lado izquierdo de la ecuación (7) sea cero para una selección arbitraria de variaciones independientes\(\ \delta q_{j}\), las expresiones entre corchetes, para cada\(\ j\), deberían ser iguales a cero. Esto nos da el conjunto deseado de\(\ J \leq 3 N\) ecuaciones

\[\ \sum_{k} m_{k} \dot{\mathbf{v}}_{k} \cdot \frac{\partial \mathbf{r}_{k}}{\partial q_{j}}-\mathscr{F}_{j}=0;\]

lo que queda es sólo refundirlos de una forma más conveniente.

Primero, usando la diferenciación por partes para calcular la siguiente derivada de tiempo:\[\frac{d}{d t}\left(\mathbf{v}_{k} \cdot \frac{\partial \mathbf{r}_{k}}{\partial q_{j}}\right)=\dot{\mathbf{v}}_{k} \cdot \frac{\partial \mathbf{r}_{k}}{\partial q_{j}}+\mathbf{v}_{k} \cdot \frac{d}{d t}\left(\frac{\partial \mathbf{r}_{k}}{\partial q_{j}}\right),\] podemos notar que el primer término en el lado derecho es exactamente el producto escalar en el primer término de la Ec. (9).

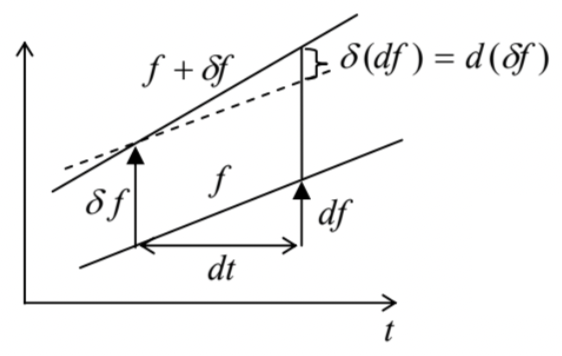
En segundo lugar, utilicemos otro dato clave del cálculo de las variaciones (que es, esencialmente, evidente a partir de la Figura 3): la diferenciación de una variable a lo largo del tiempo y sobre la variación de coordenadas generalizada (en un tiempo fijo) son operaciones intercambiables. Como resultado, en el segundo término del lado derecho de la Ec. (10) podemos escribir\[\frac{d}{d t}\left(\frac{\partial \mathbf{r}_{k}}{\partial q_{j}}\right)=\frac{\partial}{\partial q_{j}}\left(\frac{d \mathbf{r}_{k}}{d t}\right) \equiv \frac{\partial \mathbf{v}_{k}}{\partial q_{j}}\]

Figura 2.3. La variación del diferencial (de cualquier función suave\(f\)) es igual al diferencial de su variación.

Finalmente, diferenciemos la ecuación (1) a lo largo del tiempo:\[\mathbf{v}_{k} \equiv \frac{d \mathbf{r}_{k}}{d t}=\sum_{j} \frac{\partial \mathbf{r}_{k}}{\partial q_{j}} \dot{q}_{j}+\frac{\partial \mathbf{r}_{k}}{\partial t} .\] Esta ecuación muestra que las velocidades de las partículas\(\mathbf{v}_{k}\) pueden considerarse como funciones lineales de las velocidades generalizadas\(\dot{q}_{j}\) consideradas como variables independientes, con coeficientes de proporcionalidad\[\frac{\partial \mathbf{v}_{k}}{\partial \dot{q}_{j}}=\frac{\partial \mathbf{r}_{k}}{\partial q_{j}} .\] Con la cuenta de las ecuaciones (10), (11), y (13), Eq. (9) se convierte en\[\frac{d}{d t} \sum_{k} m_{k} \mathbf{v}_{k} \cdot \frac{\partial \mathbf{v}_{k}}{\partial \dot{q}_{j}}-\sum_{k} m_{k} \mathbf{v}_{k} \cdot \frac{\partial \mathbf{v}_{k}}{\partial q_{j}}-\mathscr{F}_{j}=0\] Este resultado puede simplificarse aún más haciendo, para la energía cinética total del sistema,\[T \equiv \sum_{k} \frac{m_{k}}{2} v_{k}^{2}=\frac{1}{2} \sum_{k} m_{k} \mathbf{v}_{k} \cdot \mathbf{v}_{k},\] el mismo compromiso que para\(\mathbf{v}_{k}\), es decir, considerando\(T\) una función no solo de las coordenadas generalizadas\(q_{j}\) y el tiempo\(t\) sino también de las velocidades generalizadas\(\dot{q}_{i}-\) como variables independientes de\(q_{j}\) y\(t\). Entonces podemos calcular las derivadas parciales de\(T\) as\[\frac{\partial T}{\partial q_{j}}=\sum_{k} m_{k} \mathbf{v}_{k} \cdot \frac{\partial \mathbf{v}_{k}}{\partial q_{j}}, \quad \frac{\partial T}{\partial \dot{q}_{j}}=\sum_{k} m_{k} \mathbf{v}_{k} \cdot \frac{\partial \mathbf{v}_{k}}{\partial \dot{q}_{j}}\] y notar que son exactamente las dos sumas que participan en la Ec. (14). Como resultado, obtenemos un sistema de ecuaciones de\(J\) Lagrange,\({ }^{7}\)\[\frac{d}{d t} \frac{\partial T}{\partial \dot{q}_{j}}-\frac{\partial T}{\partial q_{j}}-\mathscr{F}_{j}=0, \quad \text { for } j=1,2, \ldots, J\] Su gran ventaja sobre las ecuaciones iniciales de la ley de Newton (4) es que las ecuaciones de Lagrange no incluyen las fuerzas de restricción\(\mathbf{N}_{k}\), y por lo tanto solo hay\(J\) de ellas, típicamente mucho menos que \(3 N\).

Esto es lo más lejos que podemos llegar para las fuerzas arbitrarias. Sin embargo, si todas las fuerzas pueden expresarse en la forma similar a, pero algo más general que la Ec. (1.22)\(\mathbf{F}_{k}=-\nabla_{k} U\left(\mathbf{r}_{1}, \mathbf{r}_{2}, \ldots, \mathbf{r}_{N}, t\right)\), donde\(U\) está la energía potencial efectiva del sistema,\({ }^{8}\) y\(\nabla_{k}\) denota la diferenciación espacial sobre las coordenadas de la\(k^{\text {th }}\) partícula, podemos refundir Eq. (8) en una forma más simple:\[\mathscr{T}_{j} \equiv \sum_{k} \mathbf{F}_{k} \cdot \frac{\partial \mathbf{r}_{k}}{\partial q_{j}}=-\sum_{k}\left(\frac{\partial U}{\partial x_{k}} \frac{\partial x_{k}}{\partial q_{j}}+\frac{\partial U}{\partial y_{k}} \frac{\partial y_{k}}{\partial q_{j}}+\frac{\partial U}{\partial z_{i}} \frac{\partial z_{i}}{\partial q_{j}}\right) \equiv-\frac{\partial U}{\partial q_{j}} .\] Ya que suponemos que eso\(U\) depende solo de las coordenadas de las partículas (y posiblemente del tiempo)\(\partial U / \partial \dot{q}_{j}=0\), pero no de las velocidades:, con la sustitución de la Ec. (18), la ecuación de Lagrange (17) puede representarse en la llamada forma canónica:\[\frac{d}{d t} \frac{\partial L}{\partial \dot{q}_{j}}-\frac{\partial L}{\partial q_{j}}=0,\] donde\(L\) está la función lagrangiana (a veces llamada solo la “lagrangiana”), definida como\[L \equiv T-U \text {. }\] (Es crucial distinguir esta función de la energía mecánica\((1.26), E=T+U\).)

Obsérvese también que de acuerdo con la Ec. (2.18), para un sistema bajo el efecto de una fuerza externa generalizada adicional\(\mathscr{T}_{j}(t)\) tenemos que utilizar, en todas estas relaciones, no la energía potencial interna\(U^{\text {(int) }}\) del sistema, sino su energía potencial Gibbs\(U \equiv U^{(\text {int })}-\mathscr{J}_{j} q_{j}-\) ver la discusión en la Sec. 1.4.

Usando el enfoque lagrangiano en la práctica, el lector siempre debe recordar que, primero, cada sistema tiene una sola función Lagrange (19b), pero es descrito por ecuaciones de\(J \geq 1\) Lagrange (19a), con\(j\) tomar valores\(1,2, \ldots, J\), y segundo, que diferenciando la función\(L\), tenemos que considerar las velocidades generalizadas como sus argumentos independientes, ignorando el hecho de que en realidad son las derivadas temporales de las coordenadas generalizadas.

---

\({ }^{1}\)Posiblemente, el contraejemplo más simple de una restricción no holonómica es un conjunto de desigualdades que describen las paredes duras que confinan el movimiento de las partículas en un volumen cerrado. Las restricciones no holonómicas se tratan mejor con otros métodos, por ejemplo, imponiendo condiciones de límite adecuadas en el movimiento (de otro modo no restringido).

\({ }^{2}\)Véase, por ejemplo, MA Ec. (10.7).

\({ }^{3}\)Para una introducción concisa al campo ver, por ejemplo, ya sea I. Gelfand y S. Fomin, Cálculo de variaciones, Dover, 2000, o L. Elsgolc, Cálculo de variaciones, Dover, 2007. Una revisión aún más corta se puede encontrar en el Capítulo 17 de Arfken y Weber - ver MA Sec. 16. Para una discusión más detallada, usando muchos ejemplos de la física, ver R. Weinstock, Cálculo de variaciones, Dover,\(2007 .\)

\({ }^{4}\)Véase, por ejemplo, MA Ec. (4.2). En todas las fórmulas de esta sección, todas las sumas superiores\(j\) son de 1 a\(J\), mientras que las sobre el número de partícula\(k\) son de 1 a\(N\), de manera que en aras de la brevedad, estos límites no se especifican explícitamente.

\({ }^{5}\)Fue explicado en una obra de 1743 de Jean le Rond d'Alembert, aunque el núcleo de este resultado se remonta a una obra anterior de Jacob (Jean) Bernoulli (1667 - 1748) -que no debe confundirse con su hijo Daniel Bernoulli (17001782) a quien se le atribuye, en particular, por la ecuación de Bernoulli para ideal fluidos, para ser discutidos en la Sec. \(8.4\)a continuación.

\({ }^{6}\)Tenga en cuenta que dado que la dimensionalidad de las coordenadas generalizadas puede ser arbitraria, la de las fuerzas generalizadas también puede diferir del newton.

\({ }^{7}\)Fueron derivados en 1788 por Joseph-Louis Lagrange, quien fue pionero en todo el campo de la mecánica analítica sin mencionar sus contribuciones clave a la teoría de números y a la mecánica celeste.

\({ }^{8}\)Tenga en cuenta que debido a la posible dependencia temporal de\(U\), la Ec. (17) no significa que las fuerzas\(\mathbf{F}_{k}\) tengan que ser conservadoras - ver la siguiente sección para mayor discusión. Con este entendimiento, seguiré usando para\(U\) la función el nombre conveniente de “energía potencial”.