2.2: Tres ejemplos simples

Como el primer ejemplo, más simple, consideremos una partícula restringida a moverse a lo largo de un eje (digamos,\(x\)):\[T=\frac{m}{2} \dot{x}^{2}, \quad U=U(x, t) .\] En este caso, es natural considerar\(x\) como la (única) coordenada generalizada, y\(\dot{x}\) como la velocidad generalizada, de manera que\[L \equiv T-U=\frac{m}{2} \dot{x}^{2}-U(x, t) .\] Considerando\(\dot{x}\) como una variable independiente, obtenemos\(\partial L / \partial \dot{x}=m \dot{x}\), y\(\partial L / \partial x=-\partial U / \partial x\), así que la Ec. (19) (¡la única ecuación de Lagrange en este caso del grado único de libertad!) rendimientos

\[\frac{d}{d t}(m \dot{x})-\left(-\frac{\partial U}{\partial x}\right)=0\]evidentemente el mismo resultado que el\(x\) -componente de la ley\(2^{\text {nd }}\) Newton con\(F_{x}=-\partial U / \partial x\). Este ejemplo es un buen chequeo de cordura, pero también muestra que el formalismo Lagrange no aporta demasiada ventaja en este caso en particular.

Tal ventaja es, sin embargo, evidente para nuestro problema del banco de pruebas - ver Figura 1. En efecto, tomando el ángulo polar\(\theta\) para la (única) coordenada generalizada, vemos que en este caso, la energía cinética depende no solo de la velocidad generalizada sino también de la coordenada generalizada: 9\[\begin{aligned} &T=\frac{m}{2} R^{2}\left(\dot{\theta}^{2}+\omega^{2} \sin ^{2} \theta\right), \quad U=-m g z+\text { const } \equiv-m g R \cos \theta+\text { const }, \\ &L \equiv T-U=\frac{m}{2} R^{2}\left(\dot{\theta}^{2}+\omega^{2} \sin ^{2} \theta\right)+m g R \cos \theta+\text { const. } \end{aligned}\] Aquí es especialmente importante recordar que al fundamentar la ecuación de Lagrange ,\(\theta\) y\(\dot{\theta}\) tienen que ser tratados como argumentos independientes de\(L\), de manera que\[\frac{\partial L}{\partial \dot{\theta}}=m R^{2} \dot{\theta}, \quad \frac{\partial L}{\partial \theta}=m R^{2} \omega^{2} \sin \theta \cos \theta-m g R \sin \theta,\] dándonos la siguiente ecuación de movimiento:\[\frac{d}{d t}\left(m R^{2} \dot{\theta}\right)-\left(m R^{2} \omega^{2} \sin \theta \cos \theta-m g R \sin \theta\right)=0 .\] Como comprobación de cordura, at\(\omega=0\), Eq. (25) se reduce a la ecuación (1.18) del péndulo habitual:\[\ddot{\theta}+\Omega^{2} \sin \theta=0, \quad \text { where } \Omega \equiv\left(\frac{g}{R}\right)^{1 / 2} .\] Exploraremos la dinámica completa ecuación (25) con más detalle más adelante, pero tenga en cuenta lo simple que fue su derivación, en comparación con escribir la ley 3D Newton y luego excluir la fuerza de reacción.

A continuación, aunque el formalismo lagrangiano se derivó de la ley Newton para sistemas mecánicos, las ecuaciones resultantes (19) son aplicables a otros sistemas dinámicos, especialmente aquellos para los que las energías cinéticas y potenciales pueden expresarse fácilmente a través de algunas coordenadas generalizadas. Como ejemplo más simple, considere la conocida conexión (Figura 4) de un condensador con capacitancia\(C\) a una bobina inductiva con autoinductancia\(\mathscr{L}^{0}\) (los ingenieros eléctricos lo llaman frecuentemente el circuito\(L C\) del tanque).

Figura 2.4. \(L C\)circuito de tanque.

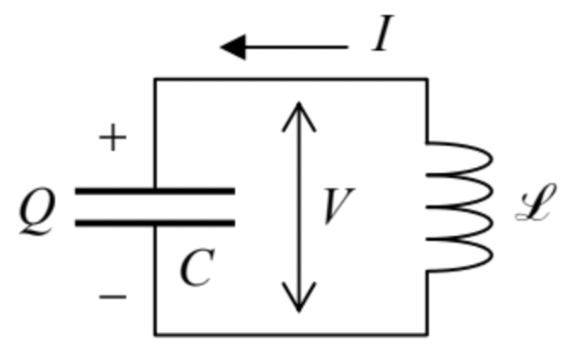
Como sabe el lector (ojalá: -), a frecuencias relativamente bajas podemos usar la llamada aproximación de circuito agrupado, en la que la energía total del sistema es la suma de dos componentes, la energía eléctrica\(E_{\mathrm{e}}\) localizada dentro del condensador, y la energía magnética\(E_{\mathrm{m}}\) localizada dentro del bobina de inductancia:\[E_{\mathrm{e}}=\frac{Q^{2}}{2 C}, \quad E_{\mathrm{m}}=\frac{\mathscr{L} I^{2}}{2} .\] Dado que la corriente eléctrica\(I\) a través de la bobina y la carga eléctrica\(Q\) en el condensador están conectadas por la ecuación de continuidad de carga\(d Q / d t=I\) (evidente a partir de la Figura 4), es natural declarar la carga como la coordenada generalizada del sistema, y corriente, su velocidad generalizada. Con esta elección, la energía electrostática\(E_{\mathrm{e}}(Q)\) puede tratarse como la energía potencial\(U\) del sistema, y la energía magnética\(E_{\mathrm{m}}(I)\), como su energía cinética\(T\). Con esta atribución, obtenemos\[\frac{\partial T}{\partial \dot{q}} \equiv \frac{\partial E_{\mathrm{m}}}{\partial I}=\mathscr{L} I \equiv \mathscr{L} \dot{Q}, \quad \frac{\partial T}{\partial q} \equiv \frac{\partial E_{\mathrm{m}}}{\partial Q}=0, \quad \frac{\partial U}{\partial q} \equiv \frac{\partial E_{\mathrm{e}}}{\partial Q}=\frac{Q}{C},\] para que la ecuación de Lagrange (19) se convierta en\[\frac{d}{d t}(\mathscr{L} \dot{Q})-\left(-\frac{Q}{C}\right)=0 .\] Note, sin embargo, que la elección anterior de la coordenada generalizada y la velocidad no es única. En cambio, se puede utilizar, como coordenada generalizada, el flujo magnético\(\Phi\) a través de la bobina inductiva, relacionado con la tensión común a\(V\) través del circuito (Figura 4) por la ley de inducción de Faraday\(V=-d \Phi / d t\). Con esta elección,\((-V)\) se convierte la velocidad generalizada,\(E_{\mathrm{m}}=\Phi^{2} / 2 \mathscr{L}\) debe ser entendida como la energía potencial, y\(E_{\mathrm{e}}=C V^{2} / 2\) tratada como la energía cinética. Para esta elección, la ecuación de movimiento de Lagrange resultante es equivalente a la Ec. (29). Si ambos parámetros del circuito,\(\mathscr{L}\) y\(C\), son constantes en el tiempo, la ecuación (29) es solo la ecuación del oscilador armónico y describe las oscilaciones sinusoidales con la frecuencia.\[\omega_{0}=\frac{1}{(\mathscr{C} C)^{1 / 2}} .\] Esto es, por supuesto, un resultado bien conocido, que puede derivarse de una manera más estándar, al igualar el caídas de voltaje a través del condensador\((V=Q / C)\) y el inductor\(\left(V=-\mathscr{L} d I / d t \equiv-\mathscr{l} d^{2} Q / d t^{2}\right)\). Sin embargo, el enfoque lagrangiano es mucho más conveniente para sistemas más complejos, por ejemplo, para la descripción general del campo electromagnético y su interacción con partículas cargadas. \({ }^{11}\)

---

\({ }^{9}\)La expresión anterior para\(T \equiv(m / 2)\left(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2}\right)\) puede obtenerse fácilmente ya sea por la diferenciación formal de la ecuación (2) a lo largo del tiempo, o simplemente al notar que el vector de velocidad tiene dos componentes perpendiculares: uno (de magnitud\(R \dot{\theta}\)) a lo largo del anillo, y otro (de magnitud\(\omega \rho=\omega R \sin \theta\)) normal a el avión del anillo.

\({ }^{10}\)Aquí se usa una fuente elegante para evitar cualquier posibilidad de confusión entre la inductancia y la función Lagrange.

\({ }^{11}\)Véase, por ejemplo, EM Secs. \(9.7\)y 9.8.