2.5: Problemas de ejercicio

En cada uno de los Problemas 2.1-2.11, para el sistema dado:

i) introducir un conjunto de coordenadas generalizadas convenientes\(q_{j}\),

ii) anotar el lagrangiano\(L\) en función de\(q_{j}, \dot{q}_{j}\), y (en su caso) el tiempo,

iii) anotar la (s) ecuación (s) de movimiento de Lagrange,

iv) calcular la función hamiltoniana\(H\); averiguar si se conserva,

v) calcular la energía\(E\);\(E=H\) ¿es? ; ¿se conserva la energía?

vi) ¿alguna otra integral evidente del movimiento?

2.1. Un péndulo doble - ver la figura a la derecha. Considera solo el movimiento en el plano vertical que contiene el punto de suspensión.

2.2. Un péndulo estirable (es decir, una partícula masiva colgada de un cordón elástico que ejerce fuerza\(F=-\kappa\left(l-l_{0}\right)\), donde\(\kappa\) y\(l_{0}\) son constantes positivas), también confinado al plano vertical:

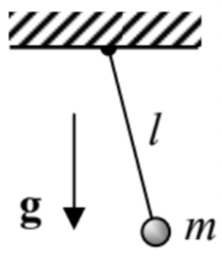
2.3. Un péndulo de longitud fija que cuelga de un soporte horizontal cuya ley de movimiento\(\ x_{0}(t)\) es fija. (Aquí no hay restricción de plano vertical).

2.4. Un péndulo de masa\(m\), colgado de otra masa puntual\(m\) ', que puede deslizarse, sin fricción, a lo largo de un riel horizontal recto - ver la figura a la derecha. El movimiento se limita al plano vertical que contiene el riel.

2.5. Un péndulo punto-masa de longitud\(l\), unido al borde de un disco de radio\(R\), que se gira en un plano vertical con una velocidad angular constante\(\omega\) - ver la figura a la derecha. (Considere solo el movimiento dentro del plano del disco).

2.6. Un cordón de masa\(m\), deslizándose sin fricción a lo largo de una cuerda ligera estirada por una fuerza fija\(\mathscr{T}\) entre dos puntos desplazados horizontalmente\(-\) ver la figura a la derecha. Aquí, en contraste con el similar Problema 1.10, la tensión de la cuerda\(\mathscr{T}\) puede ser comparable con el peso del cordón\(m g\), y el movimiento no se restringe al plano vertical.

2.7. Un cordón de masa\(m\), deslizándose sin fricción a lo largo de una cuerda ligera de una longitud fija\(2 l\), la cual se cuelga entre dos puntos, desplazada horizontalmente por la distancia\(2 d<2 l-\) ver la figura a la derecha. Como en el problema anterior, el movimiento no se restringe al plano vertical.

2.8. Un bloque de masa\(m\) que puede deslizarse, sin fricción, a lo largo de la superficie plana inclinada de una cuña pesada con masa\(m\) '. La cuña es libre de moverse, también sin fricción, a lo largo de una superficie horizontal - vea la figura a la derecha. (Ambos movimientos están dentro del plano vertical que contiene la línea de pendiente más pronunciada).

2.9. El sistema de dos péndula que fue objeto del Problema 1.8 — ver la figura de la derecha.

2.10. Un sistema de dos\(\ LC\) circuitos similares acoplados inductivamente — vea la figura de la derecha.

2.11.* Una pequeña unión Josephson -el sistema que consiste en dos superconductores (S) débilmente acoplados por túnel Cooper-pair a través de una fina capa aislante (I) que los separa - ver la figura a la derecha.

Consejos:

(i) A frecuencias no muy altas (cuya cuántica\(\hbar \omega\) es menor que la energía\(2 \Delta\) de unión de los pares Cooper), el efecto Josephson en una unión suficientemente pequeña puede describirse mediante la siguiente energía de acoplamiento:\[U(\varphi)=-E_{\mathrm{J}} \cos \varphi+\text { const }\] donde la constante\(E_{J}\) describe la fuerza de acoplamiento, mientras que la variable\(\varphi\) (llamada diferencia de fase Josephson) está conectada al voltaje a\(V\) través de la unión por la famosa relación frecuencia-voltaje\[\frac{d \varphi}{d t}=\frac{2 e}{\hbar} V,\] donde\(e \approx 1.602 \times 10^{-19} \mathrm{C}\) está la carga eléctrica fundamental y\(\hbar \approx 1.054 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\) es la constante de Planck. \({ }^{18}\)

(ii) La unión (como cualquier sistema de dos conductores cercanos) tiene una capacitancia eléctrica sustancial\(C\).

---

\({ }^{18}\)Se\(\varphi\) puede encontrar más discusión sobre el efecto Josephson y el sentido físico de la variable, por ejemplo, en EM Sec. \(6.5\)y QM Secs. \(1.6\)y\(2.8\) de esta serie de notas de conferencia, pero el problema dado puede resolverse sin esa información adicional.