3.6: Problemas de ejercicio

3.1. Para el sistema considerado en Problem\(2.6\) (un cordón que se desliza a lo largo de una cuerda con tensión fija\(\mathscr{F}\), ver la figura a la derecha), analice pequeñas oscilaciones de la cuenta cerca del equilibrio.

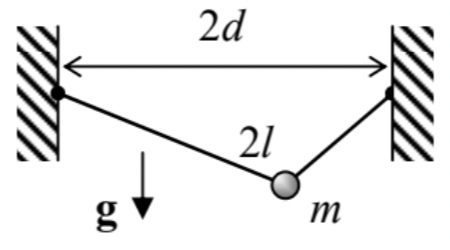
3.2. Para el sistema considerado en Problem\(2.7\) (un cordón que se desliza a lo largo de una cuerda de una longitud fija\(2 l\), ver la figura de la derecha), analice pequeñas oscilaciones cerca del equilibrio.

3.3. Para una partícula 1D de masa\(m\), colocada en potencial\(U(q)=\alpha q^{2 n}\) (donde\(\alpha>0\), y\(n\) es un entero positivo), calcular la dependencia funcional del período de oscilación de la partícula\(\tau\) en su energía\(E\). Explora el límite\(n \rightarrow \infty\).

3.4. Explique por qué el término\(m r^{2} \dot{\varphi}^{2} / 2\), refundida de acuerdo con la Ec. (42), no puede fusionarse con\(U(r)\) en la Ec. (38), para formar una energía potencial 1D efectiva\(U(r)-L_{z}^{2} / 2 m r^{2}\), con el signo del segundo término opuesto al dado por la Ec. (44). Hemos hecho algo aparentemente similar para nuestro banco de pruebas, problema de anillo giratorio con cuentas al final de la Sec. 1 - ver Eq. (6); ¿por qué no puede funcionar el mismo truco para el problema planetario? Además de una explicación formal, discuta la física detrás de esta diferencia.

3.5. Un sistema que consta de dos masas iguales\(m\) sobre una varilla ligera de longitud\(l\) (frecuentemente llamada mancuerna) puede deslizarse sin fricción a lo largo de un anillo vertical de radio\(R\), girado alrededor de su diámetro vertical con velocidad angular constante\(\omega-\) ver la figura a la derecha. Derivar la condición de estabilidad de la posición horizontal inferior de la mancuerna.

3.6. Analizar la dinámica del llamado péndulo esférico - una masa puntual colgada, en un campo de gravedad uniforme\(\mathbf{g}\), sobre un cordón ligero de longitud\(l\), sin confinamiento de movimiento a un plano vertical. En particular:

(i) encontrar las integrales de movimiento y reducir el problema a\(1 \mathrm{D}\) uno,

(ii) calcular el periodo de tiempo del posible movimiento circular alrededor del eje vertical, y

(iii) explorar pequeñas desviaciones del movimiento circular. (¿Están cerradas las órbitas del péndulo?) \({ }^{27}\)

3.7. Las órbitas de Marte y la Tierra alrededor del Sol pueden estar bien aproximadas como círculos, con una relación de radios de\(3 / 2\). Usa este hecho, y la duración del año de la Tierra (que debes saber: -), para calcular el tiempo de viaje a Marte gastando la menor cantidad de energía para el lanzamiento de una nave espacial. Descuidar el tamaño de los planetas y los efectos de sus campos gravitacionales.

3.8. Derivar ecuaciones diferenciales de primer orden y segundo orden para la distancia\(u \equiv 1 / r\) recíproca en función de\(\varphi\), describiendo la trayectoria del movimiento de las partículas en un potencial central\(U(r)\). Deletrear esta última ecuación para el caso particular del potencial de Coulomb (49) y discutir el resultado.

3.9. Para el movimiento de una partícula en el campo atractivo de Coulomb (con potencial\(U(r)=-\alpha / r\), con\(\alpha>0\)), calcular y bosquejar la llamada hodografía\(^{28}-\) la trayectoria seguida por la cabeza del vector de velocidad\(\mathbf{v}\), siempre que su cola se mantenga en el origen.

3.10. Para el movimiento en el siguiente potencial central:\[U(r)=-\frac{\alpha}{r}+\frac{\beta}{r^{2}},\] (i) encontrar la órbita\(r(\varphi)\), para positivo\(\alpha\) y\(\beta\), y todos los rangos posibles de energía\(E\);

ii) demostrar que en el límite\(\beta \rightarrow 0\), y para la energía\(E<0\), la órbita puede representarse como una elipse que gira lentamente;

(iii) expresar la velocidad angular de esta rotación orbital lenta a través de los parámetros\(\alpha\) y\(\beta\), la masa de la partícula\(m\), su energía\(E\) y el momento angular\(L_{z}\).

3.11. Una partícula se mueve en el campo de una fuerza central atractiva, con potencial ¿\[U(r)=-\frac{\alpha}{r^{n}}, \quad \text { where } \alpha n>0 .\] Para qué valores de\(n\) es estable una órbita circular?

3.12. Determinar la condición para que una partícula de masa\(m\), que se mueve bajo el efecto de una fuerza central de atracción\[\mathbf{F}=-\alpha \frac{\mathbf{r}}{r^{3}} \exp \left\{-\frac{r}{R}\right\},\] donde\(\alpha\) y\(R\) son constantes positivas, tenga una órbita circular estable.

3.13. Una partícula de masa\(m\), con momento angular\(L_{z}\), se mueve en el campo de una fuerza central atractiva con una magnitud independiente de la distancia\(F\). Si la energía de la partícula\(E\) es ligeramente superior al valor\(E_{\min }\) correspondiente a la órbita circular de la partícula, ¿cuál es el periodo de tiempo de sus oscilaciones radiales? Comparar el periodo con el de la órbita circular en\(E=E_{\min }\).

3.14. Para la dispersión de partículas por un campo repulsivo de Coulomb, calcule la distancia mínima de aproximación\(r_{\min }\) y la velocidad\(v_{\min }\) en ese punto, y analice su dependencia del parámetro de impacto\(b\) (ver Figura 9) y la velocidad inicial\(v_{\infty}\) de la partícula.

3.15. Una partícula se lanza desde lejos, con parámetro de impacto\(b\), hacia un centro de atracción con\[U(r)=-\frac{\alpha}{r^{n}}, \quad \text { with } n>2, \alpha>0 .\] (i) Expresar la distancia mínima entre la partícula y el centro vía\(b\), si la energía cinética inicial\(E\) de la partícula es apenas suficiente para escapar de su captura por el centro de atracción.

(ii) Calcular la sección transversal total de la captura; explorar el límite\(n \rightarrow 2\).

3.16. Un meteorito con velocidad inicial\(v_{\infty}\) se acerca a un planeta libre de atmósfera de masa\(M\) y radio\(R\).

(i) Encontrar la condición en el parámetro de impacto\(b\) para que el meteorito golpee la superficie del planeta.

(ii) Si el meteorito apenas evita la colisión, ¿cuál es su ángulo de dispersión?

3.17. Calcular las secciones transversales diferenciales y totales de la dispersión elástica clásica de pequeñas partículas por una esfera dura de radio\(R\).

3.18. La\({ }^{29}\) confirmación más famosa de la teoría de la relatividad general de Einstein proviene de la observación, por parte de A. Eddington y sus asociados, de la desviación de la luz estelar por el Sol, durante el eclipse solar de mayo de 1919. Considerando los fotones de luz como partículas clásicas que se propagan con la velocidad de la luz\(v_{0} \rightarrow c \approx 3.00 \times 10^{8} \mathrm{~m} / \mathrm{s}\), y los datos astronómicos para la masa del Sol\(M_{\mathrm{S}} \approx 1.99 \times 10^{30} \mathrm{~kg}\), y el radio\(R_{\mathrm{S}} \approx\)\(6.96 \times 10^{8} \mathrm{~m}\), calculan la predicción de la mecánica no relativista para la desviación angular de los rayos de luz que rozan la superficie del Sol.

---

\({ }^{27}\)Resolver este problema es una muy buena preparación para el análisis de la rotación de los cimas simétricos en el siguiente capítulo.

\({ }^{28}\)El uso de esta noción para la caracterización del movimiento se remonta al menos a un tratado de 1846 de W. Hamilton. Hoy en día, se utiliza con mayor frecuencia en mecánica de fluidos aplicada, en particular meteorología.

\({ }^{29}\)Sin embargo, no fue la primera confirmación. El primero vino cuatro años antes del propio Albert Einstein, quien demostró que su teoría puede explicar cualitativamente la diferencia entre la tasa de precesión de la órbita de Mercurio, conocida por observaciones anteriores, y la teoría no relativista de ese efecto.