6.1: Dos osciladores acoplados

Discutamos las oscilaciones en sistemas con varios grados de libertad, partiendo del caso más simple de dos osciladores 1D lineales (armónicos), libres de disipación. Si los osciladores son independientes entre sí, la función lagrangiana de su sistema puede representarse como una suma de dos términos independientes del tipo (5.1):\[L=L_{1}+L_{2}, \quad L_{1,2}=T_{1,2}-U_{1,2}=\frac{m_{1,2}}{2} \dot{q}_{1,2}^{2}-\frac{\kappa_{1,2}}{2} q_{1,2}^{2} .\] Correspondientemente, Ecuaciones (2.19) para\(q_{j}=q_{1,2}\) rendimientos dos ecuaciones independientes de movimiento de los osciladores, siendo cada una similar a la Ec. (5) .2):\[m_{1,2} \ddot{q}_{1,2}+m_{1,2} \Omega_{1,2}^{2} q_{1,2}=0, \quad \text { where } \Omega_{1,2}^{2}=\frac{\kappa_{1,2}}{m_{1,2}} .\] (En el contexto de lo que sigue, a veces\(\Omega_{1,2}\) se llaman las frecuencias parciales.) Esto significa que en este caso más simple, un movimiento arbitrario del sistema es solo una suma de oscilaciones sinusoidales independientes a dos frecuencias iguales a las frecuencias parciales (2).

Sin embargo, tan pronto como los osciladores se acoplan (es decir, interactúan), el Lagrangiano completo\(L\) contiene un término mixto adicional\(L_{\text {int }}\) dependiendo de las coordenadas\(q_{1}\) generalizadas\(q_{2}\) y/o velocidades generalizadas. Como ejemplo sencillo, consideremos el sistema mostrado en la Figura 1, allí dos pequeñas masas\(m_{1,2}\) están obligadas a moverse en una sola dirección (mostrada horizontal), y se mantienen entre dos paredes rígidas con tres resortes.

Fig. 6.1. Un sistema sencillo de dos osciladores lineales acoplados.

En este caso, la energía cinética sigue siendo separable\(T=T_{1}+T_{2}\), pero la energía potencial total, que consiste en las energías elásticas de tres resortes, no lo es:\[U=\frac{\kappa_{\mathrm{L}}}{2} q_{1}^{2}+\frac{\kappa_{\mathrm{M}}}{2}\left(q_{1}-q_{2}\right)^{2}+\frac{\kappa_{\mathrm{R}}}{2} q_{2}^{2},\] dónde\(q_{1.2}\) están los desplazamientos horizontales de las partículas desde sus posiciones de equilibrio. Es conveniente reescribir esta expresión ya que\[U=\frac{\kappa_{1}}{2} q_{1}^{2}+\frac{\kappa_{2}}{2} q_{2}^{2}-\kappa q_{1} q_{2}, \quad \text { where } \kappa_{1} \equiv \kappa_{\mathrm{L}}+\kappa_{\mathrm{M}}, \quad \kappa_{2} \equiv \kappa_{\mathrm{R}}+\kappa_{\mathrm{M}}, \quad \kappa \equiv \kappa_{\mathrm{M}},\] muestra que la función lagrangiana\(L=T-U\) de este sistema contiene, además de los términos parciales (1), un término de interacción\[L=L_{1}+L_{2}+L_{\text {int }}, \quad L_{\text {int }}=\kappa q_{1} q_{2} .\] bilineal: Las ecuaciones de movimiento de Lagrange resultantes son\[\begin{aligned} &m_{1} \ddot{q}_{1}+m_{1} \Omega_{1}^{2} q_{1}=\kappa q_{2}, \\ &m_{2} \ddot{q}_{2}+m_{2} \Omega_{2}^{2} q_{2}=\kappa q_{1} . \end{aligned}\] Así la interacción conduce a una efectiva la fuerza generalizada\(\kappa q_{2}\) ejercida sobre el subsistema 1 por el subsistema 2, y la fuerza efectiva recíproca\(\kappa q_{1}\).

Tenga en cuenta dos aspectos importantes de este sistema de ecuaciones (por lo demás bastante simple). Primero, en contraste con las fuerzas de interacción física reales (como\(F_{12}=-F_{21}=\kappa_{\mathrm{M}}\left(q_{2}-q_{1}\right)\) para nuestro sistema\(^{1}\)), las fuerzas efectivas en los lados derecho de las ecuaciones (5) no obedecen a la ley de\(3^{\text {rd }}\) Newton. Segundo, las fuerzas son proporcionales al mismo coeficiente\(\kappa\), esta característica es resultado de la estructura bilineal general (4) de la energía de interacción, más que de cualquier simetría especial.

De nuestras discusiones previas, ya sabemos resolver las ecuaciones (5), porque sigue siendo un sistema de ecuaciones diferenciales lineales y homogéneas, por lo que su solución general es una suma de soluciones particulares de la forma similar a las ecuaciones (5.88),\[q_{1}=c_{1} e^{\lambda t}, \quad q_{2}=c_{2} e^{\lambda t},\] con todos los valores posibles de\(\lambda\). Estos valores se pueden encontrar al conectar la Eq. (6) en las ecuaciones (5), y requiriendo que el sistema resultante de dos ecuaciones algebraicas lineales homogéneas para los coeficientes de distribución\(c_{1,2}\),\[\begin{aligned} &m_{1} \lambda^{2} c_{1}+m_{1} \Omega_{1}^{2} c_{1}=\kappa c_{2} \\ &m_{2} \lambda^{2} c_{2}+m_{2} \Omega_{2}^{2} c_{2}=\kappa c_{1} \end{aligned}\] sea autoconsistente. En nuestro caso particular, obtenemos una ecuación característica,\[\left|\begin{array}{cc} m_{1}\left(\lambda^{2}+\Omega_{1}^{2}\right) & -\kappa \\ -\kappa & m_{2}\left(\lambda^{2}+\Omega_{2}^{2}\right) \end{array}\right|=0,\] que es cuadrática en\(\lambda^{2}\), y así permite una solución analítica simple:\[\left(\lambda^{2}\right)_{\pm}=-\frac{1}{2}\left(\Omega_{1}^{2}+\Omega_{2}^{2}\right) \mp\left[\frac{1}{4}\left(\Omega_{1}^{2}+\Omega_{2}^{2}\right)^{2}-\Omega_{1}^{2} \Omega_{2}^{2}+\frac{\kappa^{2}}{m_{1} m_{2}}\right]^{1 / 2}\]\[\equiv-\frac{1}{2}\left(\Omega_{1}^{2}+\Omega_{2}^{2}\right) \mp\left[\frac{1}{4}\left(\Omega_{1}^{2}-\Omega_{2}^{2}\right)^{2}+\frac{\kappa^{2}}{m_{1} m_{2}}\right]^{1 / 2} .\] Según las ecuaciones (2) y (3b), para cualquier valor positivo de constantes de resorte, el producto siempre\(\Omega_{1} \Omega_{2}=\)\(\left(\kappa_{L}+\kappa_{M}\right)\left(\kappa_{R}+\kappa_{M}\right) /\left(m_{1} m_{2}\right)^{1 / 2}\) es mayor que \(\kappa /\left(m_{1} m_{2}\right)^{1 / 2}=\kappa_{M} /\left(m_{1} m_{2}\right)^{1 / 2}\), de manera que la raíz cuadrada en la Ec. (9) es siempre menor que\(\left(\Omega_{1}{ }^{2}+\Omega_{2}{ }^{2}\right) / 2\). Como resultado, ambos valores de\(\lambda^{2}\) son negativos, es decir, la solución general a la Ec. (5) es una suma de cuatro términos, cada uno proporcional a\(\exp \left\{\pm i \omega_{\pm} t\right\}\), donde ambas frecuencias propias (“frecuencias propias”)\(\omega_{\pm} \equiv i \lambda_{\pm}\) son reales:

\[\ \text{Anticrossing description}\quad\quad\quad\quad\omega_{\pm}^{2} \equiv-\lambda_{\pm}^{2}=\frac{1}{2}\left(\Omega_{1}^{2}+\Omega_{2}^{2}\right) \pm\left[\frac{1}{4}\left(\Omega_{1}^{2}-\Omega_{2}^{2}\right)^{2}+\frac{\kappa^{2}}{m_{1} m_{2}}\right]^{1 / 2}.\]

Una gráfica de estas frecuencias propias en función de una de las frecuencias parciales (digamos,\(\Omega_{1}\)), con la otra frecuencia parcial fija, nos da el famoso diagrama anticrosante (también llamado el “cruce evitado” o “no cruce”) - ver Figura 2. Se puede ver que en acoplamiento débil, las frecuencias\(\omega_{\pm}\) están cerca de las frecuencias parciales\(\Omega_{1,2}\) en todas partes además de un rango estrecho cerca del punto anticrosante\(\Omega_{1}=\Omega_{2}\). Lo más notable es que al pasar por esta región,\(\omega_{+}\) sin problemas “cambia” de seguimiento\(\Omega_{2}\) a seguimiento\(\Omega_{1}\) y viceversa.

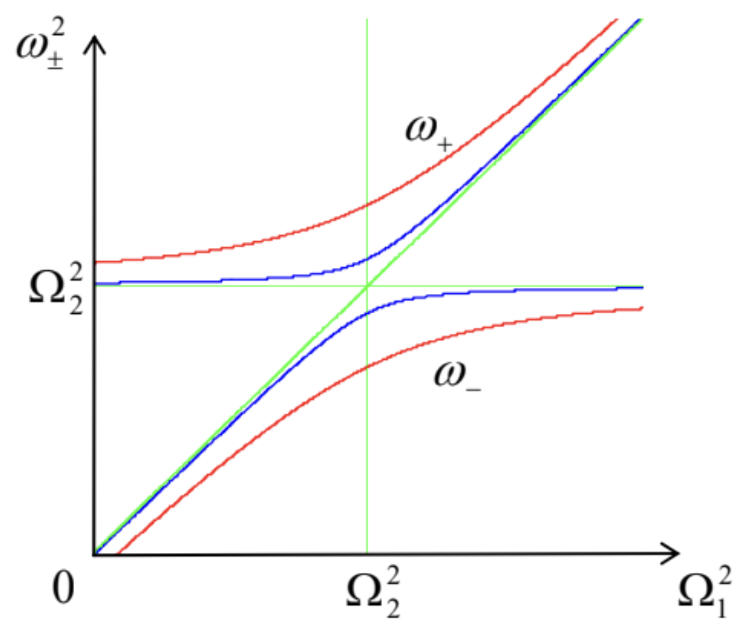
Figura 6.2. El diagrama anticrosante para dos valores de la resistencia normalizada del acoplamiento\(\kappa /\left(m_{1} m_{2}\right)^{1 / 2} \Omega_{2}^{2}: 0.3\) (líneas rojas) y\(0.1\) (líneas azules). En esta trama,\(\Omega_{1}\) se supone que se cambia variando en\(\kappa_{1}\) lugar de\(m_{1}\), pero en el caso contrario, el diagrama es cualitativamente similar.

La razón de este comportamiento contradictorio se puede encontrar examinando los coeficientes de distribución\(c_{1,2}\) correspondientes a cada rama del diagrama, los cuales se pueden obtener al enchufar el valor correspondiente de\(\lambda_{\pm}=-i \omega_{\pm}\) nuevo en las ecuaciones (7). Por ejemplo, en el punto anticrosante\(\Omega_{1}=\Omega_{2} \equiv \Omega\), la ecuación (10) se reduce a\[\omega_{\pm}^{2}=\Omega^{2} \pm \frac{\kappa}{\left(m_{1} m_{2}\right)^{1 / 2}}=\Omega^{2}\left(1 \pm \frac{\kappa}{\left(\kappa_{1} \kappa_{2}\right)^{1 / 2}}\right) .\] Tapar esta expresión de nuevo en cualquiera de las ecuaciones (7), vemos que para las dos ramas del diagrama anticrosante, la relación del coeficiente de distribución es la misma por magnitud pero opuesta por signo:\[\left(\frac{c_{1}}{c_{2}}\right)_{\pm}=\mp\left(\frac{m_{2}}{m_{1}}\right)^{1 / 2}, \text { at } \Omega_{1}=\Omega_{2} .\] En particular, si el sistema es simétrico\(\left(m_{1}=m_{2}, \kappa_{\mathrm{L}}=\kappa_{\mathrm{R}}\right)\), luego en la rama superior, correspondiente a\(\omega_{+}>\omega_{-}\), obtenemos\(c_{1}=-c_{2}\). Esto significa que en este llamado modo duro,\({ }^{2}\) las masas oscilan en antifase:\(q_{1}(t) \equiv-q_{2}(t)\). La extensión/compresión sustancial resultante del resorte medio (ver Figura 1 nuevamente) produce una fuerza de retorno adicional que aumenta la frecuencia de oscilación. Por el contrario, en la rama inferior, correspondiente a, es decir\(\omega_{\text {., the particle oscillations are in phase: } c_{1}}=c_{2}\)\(q_{1}(t) \equiv q_{2}(t)\), para que el resorte medio no se estire ni se comprima en absoluto. Como resultado, en este modo suave, la frecuencia de oscilación\(\omega_{-}\) es menor que\(\omega_{+}\), y no depende de\(\kappa_{\mathrm{M}}\):\[\omega_{-}^{2}=\Omega^{2}-\frac{\kappa}{m}=\frac{\kappa_{\mathrm{L}}}{m}=\frac{\kappa_{\mathrm{R}}}{m} .\] Tenga en cuenta que para ambos modos, las oscilaciones se acoplan igualmente a ambas partículas.

Lejos del punto anticrosante, la situación es completamente diferente. En efecto, un cálculo similar de\(c_{1,2}\) muestra que en cada rama del diagrama, la magnitud de uno de los coeficientes de distribución es mucho mayor que la de su contraparte. De ahí que en este límite, cualquier modo particular de oscilaciones implica prácticamente una sola partícula. Un cambio lento de los parámetros del sistema, llevándolo a través del anticrosamiento, da como resultado, primero, una deslocalización máxima de cada modo en\(\Omega_{1}=\Omega_{2}\), y luego en la restauración de la localización, pero en un grado parcial diferente de libertad.

Podríamos realizar fácilmente cálculos similares para el caso cuando los sistemas se acoplan a través de sus velocidades\(L_{\text {int }}=m \dot{q}_{1} \dot{q}_{2}\), donde\(m\) es un coeficiente de acoplamiento\(-\) no necesariamente una cierta masa física. \({ }^{3}\)Los resultados son generalmente similares a los discutidos anteriormente, nuevamente con la división de nivel máximo en\(\Omega_{1}=\Omega_{2} \equiv \Omega\): siendo válida\[\omega_{\pm}^{2}=\frac{\Omega^{2}}{1 \mp|m| /\left(m_{1} m_{2}\right)^{1 / 2}} \approx \Omega^{2}\left[1 \pm \frac{|m|}{\left(m_{1} m_{2}\right)^{1 / 2}}\right],\] la última relación para acoplamiento débil. La generalización al caso tanto del acoplamiento de coordenadas como de velocidad también es sencilla - ver la siguiente sección.

Obsérvese que el diagrama anticrosante, mostrado en la Figura 2, es aún más ubicuo en la mecánica cuántica, ya que, debido al carácter oscilatorio de tiempo de las soluciones de la ecuación de Schrödinger, un acoplamiento débil de dos estados cuánticos cualesquiera conduce a un comportamiento cualitativamente similar\(\omega_{\pm}\) de las frecuencias propias del sistema, y por lo tanto de sus energías propias (“niveles de energía”)\(E_{\pm}=\hbar \omega_{\pm}\) del sistema.

Una propiedad más de los osciladores débilmente acoplados, una transferencia lenta periódica de energía de un oscilador a otro y viceversa, especialmente bien pronunciada en o cerca del punto anticrosante\(\Omega_{1}=\Omega_{2}\), también es más importante para la mecánica cuántica que para la mecánica clásica. Es por ello que remito al lector a la parte QM de esta serie para una discusión detallada de este fenómeno.

---

\({ }^{1}\)Usando estas expresiones, las ecuaciones (5) pueden obtenerse fácilmente de las leyes de Newton, pero el enfoque lagrangiano utilizado anteriormente hará que su generalización, en la siguiente sección, sea más sencilla.

\({ }^{2}\)En física, el término “modo” se utiliza típicamente para describir la distribución de una variable en el espacio, en sus oscilaciones con una sola frecuencia. En nuestro caso actual, cuando la noción de espacio se reduce a dos números de oscilador, el “modo” significa solo un conjunto de dos coeficientes de distribución\(c_{1,2}\) para una frecuencia propia particular.

\({ }^{3}\)En mecánica,\(q_{1,2}\) al representar los desplazamientos lineales reales de las partículas, dicho acoplamiento no es muy natural, pero existen muchos sistemas dinámicos de naturaleza no mecánica en los que dicho acoplamiento es el más natural. El ejemplo más simple es el sistema de dos circuitos\(L C\) (“tanque”), con acoplamiento capacitivo o inductivo. En efecto, como se discutió en la Sec. 2.2, para tal sistema, las nociones mismas de las energías potenciales y cinéticas son condicionales e intercambiables.