6.8: Problemas de ejercicio

Para cada uno de los sistemas especificados en Problemas 6.1-6.6:

i) introducir convenientes coordenadas generalizadas\(q_{j}\) del sistema,

ii) calcular las frecuencias de sus pequeñas oscilaciones armónicas cercanas al equilibrio,

iii) calcular los coeficientes de distribución correspondientes, y

(iv) bosquejar los modos de oscilación.

6.1. Dos péndulos acoplados elásticamente, confinados a un plano vertical, con los parámetros mostrados en la figura a la derecha (ver también Problemas\(1.8\) y 2.9).

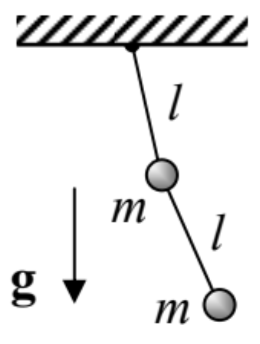
6.2. El péndulo doble, confinado a un plano vertical que contiene el punto de soporte (considerado en el Problema 2.1), con\(m^{\prime}=m\) y\(l=l^{\prime}-\) ver la figura a la derecha.

6.3. El timbre considerado en Problema\(4.8\) (ver la figura de la derecha), para el caso particular\(l=l^{\prime}\).

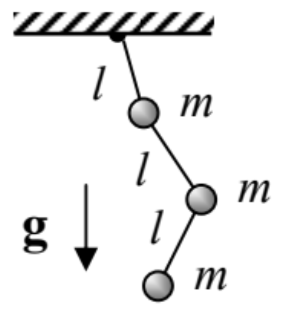
6.4. El triple péndulo que se muestra en la figura de la derecha, con el movimiento confinado a un plano vertical que contiene el punto de soporte.

Pista: Puede usar cualquier método (por ejemplo, numérico) para calcular las raíces de la ecuación característica.

6.5. Un sistema lineal y simétrico de tres partículas, mostrado en la figura de la derecha, donde las conexiones entre las partículas no solo actúan como resortes elásticos habituales (dando energías potenciales\(U=\kappa(\Delta l)^{2} / 2\)) sino que también resisten la flexión, dando energía potencial adicional\(U^{\prime}=\kappa^{\prime}(l \theta)^{2} / 2\), donde\(\theta\) está el (pequeño) ángulo de flexión. \({ }^{33}\)

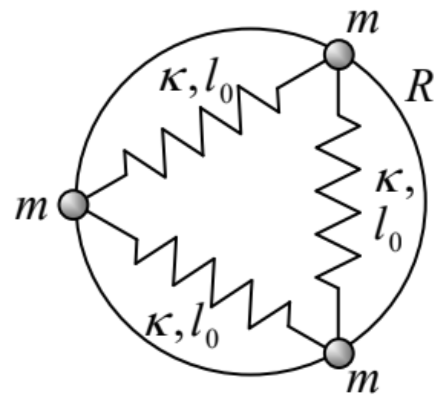
6.6. Tres cuentas similares de masa\(m\), que pueden deslizarse a lo largo de un círculo de radio\(R\) sin fricción, conectadas con resortes similares con constantes elásticas\(\kappa\) y longitudes de equilibrio\(l_{0}\) - ver la figura a la derecha.

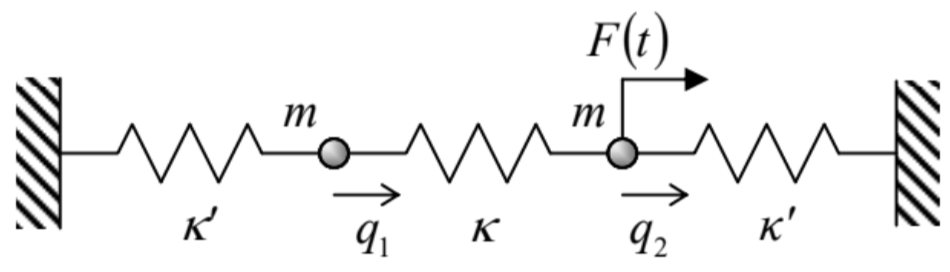
6.7. \(F(t)\)Se aplica una fuerza longitudinal externa a la partícula derecha del sistema mostrado en la Figura 1, con\(\kappa_{\mathrm{L}}=\kappa_{\mathrm{R}}=\kappa^{\prime}\) y\(m_{1}=m_{2} \equiv m\) (ver la figura de la derecha), y se está midiendo la respuesta\(q_{1}(t)\) de la\(N\) partícula izquierda a esta fuerza.

(i) Calcular la función temporal del Verde para esta respuesta.

(ii) Utilizar esta función para calcular la respuesta a la siguiente fuerza:\[F(t)= \begin{cases}0, & \text { for } t<0 \\ F_{0} \sin \omega t, & \text { for } 0 \leq t\end{cases}\] con amplitud\(F_{0}\) y frecuencia constantes\(\omega\).

\(\underline{6.8}\). Utilice el formalismo lagrangiano para volver a derivar las ecuaciones (24) tanto para las oscilaciones longitudinales como para las transversales en el sistema mostrado en la Figura\(4 \mathrm{a}\).

6.9. Calcular la energía (por unidad de longitud) de una onda itinerante sinusoidal que se propaga en el sistema 1D mostrado en la Figura 4a. Usa tu resultado para calcular el flujo de potencia promedio creado por la onda, y compararlo con la Eq. (49) válida en el límite de onda acústica.

6.10. Calcular las distribuciones espaciales de las energías cinéticas y potenciales en una onda acústica 1D sinusoidal estacionaria y analizar su evolución en el tiempo.

6.11. El punto medio de una cuerda de guitarra de longitud\(l\) ha sido arrancado lentamente por la\(h<<l\) distancia de su posición de equilibrio, para luego soltarlo. Descuidando la disipación, utilice dos enfoques diferentes para calcular el desplazamiento del punto medio en función del tiempo.

Pista: Es posible que desee utilizar las siguientes series de tablas:\[\sum_{m=1}^{\infty} \frac{\cos (2 m-1) \xi}{(2 m-1)^{2}}=\frac{\pi^{2}}{8}\left(1-\frac{\xi}{\pi / 2}\right), \quad \text { for } 0 \leq \xi \leq \pi .\]

6.12. Calcular la ley de dispersión\(\omega(k)\) y las frecuencias máxima y mínima de pequeñas ondas longitudinales en una larga cadena de péndula similar acoplada por resorte - ver la figura a la derecha.

6.13. Calcular y analizar la relación de dispersión\(\omega(k)\) para pequeñas ondas en una larga cadena de partículas acopladas elásticamente con masas alternas - ver la figura de la derecha. En particular, discutir el período de la relación de dispersión\(\Delta k\), y su evolución en\(m^{\prime} \rightarrow m\).

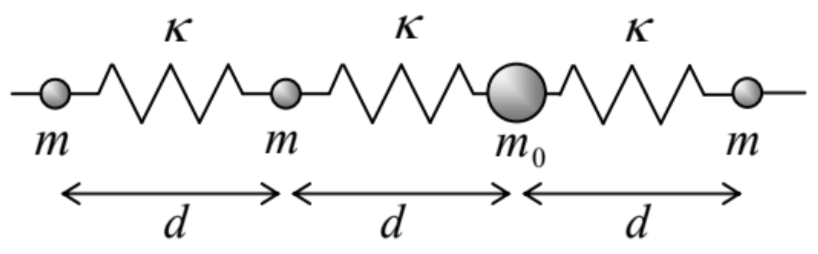
6.14. Analizar la reflexión de la onda viajera desde una “falta de homogeneidad puntual”: una sola partícula con una masa diferente\(m_{0} \neq m\), dentro de una cadena 1D por lo demás uniforme - ver la figura a la derecha.

6.15*

(i) Explorar una forma aproximada de analizar las ondas en un\(1 \mathrm{D}\) sistema continuo con parámetros que varían lentamente a lo largo de su longitud.

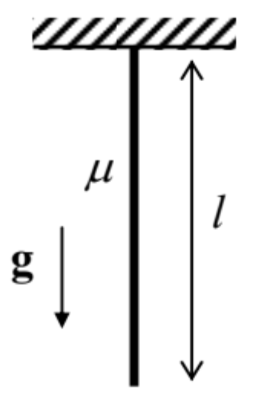
(ii) Aplicar este método para calcular las frecuencias de ondas estacionarias transversales sobre una cuerda pesada de longitud que cuelga libremente\(l\), con una masa constante\(\mu\) por unidad de longitud - ver la figura de la derecha.

(iii) Para los tres modos de onda estacionaria más bajos, compare los resultados con los obtenidos en la solución del Problema 4 para el triple péndulo.

Pista: El lector familiarizado con la aproximación WKB en mecánica cuántica (ver, por ejemplo, QM Sec. 2.4) es bienvenido a adaptarla para esta aplicación clásica. Otro posible punto de partida es la aproximación de van der Pol discutida en la Sec. 5.3, la cual debe traducirse del dominio del tiempo al dominio espacial.

6.16. \({ }^{*}\)Utilice la aproximación van der Pol para analizar el bloqueo de fase mutuo de dos autoosciladores débilmente acoplados con la no linealidad disipativa, para los casos de:

(i) el acoplamiento coordinado directo, descrito por la Ec. (5), y

ii) un acoplamiento bilineal pero arbitrario de dos osciladores similares.

Pista: En la Tarea (ii), describa el acoplamiento por un operador lineal y exprese el resultado a través de su imagen de Fourier.

6.17. \({ }^{*}\)Extender la segunda tarea del problema anterior al bloqueo de fase mutuo de autoosciladores\(N\) similares. En particular, explorar la estabilidad del modo en fase para el caso del llamado acoplamiento global a través de una sola fuerza\(F\) aportada por igual por todos los osciladores.

6.18. \({ }^{*}\)Encontrar la condición de excitación paramétrica no degenerada en un sistema de dos osciladores acoplados, descritos por las ecuaciones (5), pero con un acoplamiento dependiente del tiempo:\(\kappa \rightarrow \kappa\left(1+\mu \cos \omega_{\mathrm{p}} t\right)\), con\(\omega_{\mathrm{p}} \approx\)\(\Omega_{1}+\Omega_{2}\), y\(\kappa / m<<\left|\Omega_{2}-\Omega_{1}\right|\).

Pista: Asumiendo que la profundidad\(\mu\) de modulación\(\kappa\), el acoplamiento estático y el desintonizado son\(\xi \equiv \omega_{\mathrm{p}}-\left(\Omega_{1}+\Omega_{2}\right)\) suficientemente pequeños, use la aproximación van der Pol para cada uno de los osciladores acoplados.

6.19. Mostrar que la no linealidad cúbica del tipo\(\alpha q^{3}\) efectivamente permite la interacción paramétrica (“mezcla de cuatro ondas”) de oscilaciones con frecuencias inconmensurables relacionadas por ecuaciones (92a).

6.20. Calcular la velocidad de las ondas transversales que se propagan sobre una membrana delgada, plana y elástica, con masa\(m\) por unidad de área, pre-estirada con fuerza\(\tau\) por unidad de ancho.

---

\({ }^{33}\)Este es un buen modelo para pequeñas oscilaciones de moléculas lineales como la ahora infame\(\mathrm{CO}_{2}\).