7.1: Cepa

Como se discutió en los Capítulos 4 y 6, en un continuo, es decir, un sistema de partículas tan cercanas entre sí que se puede descuidar la discreción del sistema, el desplazamiento de partículas\(\mathbf{q}\) puede considerarse como una función continua del espacio y el tiempo. En este capítulo, consideraremos solo pequeñas desviaciones de la aproximación rígido-cuerpo discutida en el Capítulo 4, es decir, pequeñas deformaciones. La pequeñez de la deformación permite considerar el vector de desplazamiento\(\mathbf{q}\) como una función de la posición inicial (pre-deformación) de la partícula, y el tiempo\(\mathbf{r}\)\(t\), tal como se hizo en el Capítulo 6 para las ondas 1D.

La primera tarea de la teoría de la deformación es excluir de consideración los tipos de movimiento considerados en el Capítulo 4, a saber, la traslación y rotación, no relacionados con las deformaciones. Esto significa, en primer lugar, que las variables que describen las deformaciones no deben depender de la parte de la distribución del desplazamiento, es decir, independiente de la posición\(\mathbf{r}\) (es decir, es común para todo el medio), porque esa parte corresponde a un desplazamiento traslacional más que a una deformación (Figura 1a). Además, incluso ciertos desplazamientos no uniformes no contribuyen a la deformación. Por ejemplo, la Ec. (4.9) (con\(d \mathbf{r}\) reemplazada con\(d \mathbf{q}\) para cumplir con nuestra notación actual) muestra que un pequeño desplazamiento del tipo\[d \mathbf{q}_{\text {rotation }}=d \varphi \times \mathbf{r} \text {, }\] donde\(d \varphi=\omega d t\) es un vector infinitesimal común para todo el continuum, corresponde a su rotación alrededor de la dirección de ese vector, y tiene nada que ver con su deformación (Figura 1b).

Figura 7.1. Dos tipos de distribuciones de vectores de desplazamiento que no están relacionadas con la deformación: (a) traslación y (b) rotación.

Es por ello que para desarrollar una adecuada caracterización cuantitativa de la deformación, debemos comenzar por encontrar funciones adecuadas de la distribución espacial de los desplazamientos\(\mathbf{q}(\mathbf{r})\),, que existen únicamente por deformaciones. Una de esas medidas es el cambio de la distancia\(d l=|d \mathbf{r}|\) entre dos puntos cercanos:\[\left.(d l)^{2}\right|_{\text {after deformation }}-\left.(d l)^{2}\right|_{\text {before deformation }}=\sum_{j=1}^{3}\left(d r_{j}+d q_{j}\right)^{2}-\sum_{j=1}^{3}\left(d r_{j}\right)^{2}\] donde\(d q_{j}\) está el componente\(j^{\text {th }}\) cartesiano de la diferencia\(d \mathbf{q}\) entre los desplazamientos\(\mathbf{q}\) de estos puntos cercanos. Si la deformación es pequeña en el sentido\(|d \mathbf{q}|<<|d \mathbf{r}|=d l\), podemos mantener en la ecuación (2) solo los términos proporcionales a la primera potencia del vector infinitesimal\(d \mathbf{q}\):\[\left.(d l)^{2}\right|_{\text {after deformation }}-\left.(d l)^{2}\right|_{\text {before deformation }}=\sum_{j=1}^{3}\left[2 d r_{j} d q_{j}+\left(d q_{j}\right)^{2}\right] \approx 2 \sum_{j=1}^{3} d r_{j} d q_{j} .\] Dado que\(q_{j}\) es una función de tres argumentos escalares independientes\(r_{j}\), su diferencial completo (a tiempo fijo) puede ser representado como\[d q_{j}=\sum_{j^{\prime}=1}^{3} \frac{\partial q_{j}}{\partial r_{j^{\prime}}} d r_{j^{\prime}}\] Los coeficientes\(\partial q_{j} / \partial r_{j}\), pueden ser considerados como elementos de un tensor\({ }^{1}\) proporcionando una relación lineal entre los vectores\(\mathrm{d} \mathbf{r}\) y\(\mathrm{d} \mathbf{q}\). Tapando la Eq. (4) en la Ec. (2), obtenemos\[\left.(d l)^{2}\right|_{\text {after deformation }}-(d l)_{\mid \text {before deformation }}^{2}=2 \sum_{j, j^{\prime}=1}^{3} \frac{\partial q_{j}}{\partial r_{j^{\prime}}} d r_{j} d r_{j^{\prime}} .\] La conveniencia del tensor\(\partial q_{j} / \partial r_{j}\), para caracterizar deformaciones es que excluye automáticamente el desplazamiento de traslación (Figura 1a), que es independiente de\(r_{j}\). Su inconveniente es que sus componentes particulares siguen siendo afectados por la rotación del cuerpo (aunque la suma (5) no lo es). De hecho, de acuerdo con la definición del producto vectorial, la ecuación (1) puede representarse en coordenadas cartesianas como\[\left.d q_{j}\right|_{\text {rotation }}=\left(d \varphi_{j^{\prime}} r_{j^{\prime \prime}}-d \varphi_{j^{\prime \prime}} r_{j^{\prime}}\right) \varepsilon_{j j j^{\prime \prime}},\] dónde\(\varepsilon_{i j i j}\) está el símbolo Levi-Civita. Diferenciando la Ec. (6) sobre una coordenada cartesiana particular del vector\(\mathbf{r}\), y teniendo en cuenta que esta diferenciación parcial\((\partial)\) es independiente de (y por lo tanto puede intercambiarse con) la diferenciación\((d)\) sobre el ángulo de rotación\(\varphi\), obtenemos las cantidades,\[d\left(\frac{\partial q_{j}}{\partial r_{j^{\prime}}}\right)_{\text {rotation }}=-\varepsilon_{i j j^{\prime \prime}} d \varphi_{j^{\prime \prime}}, \quad d\left(\frac{\partial q_{j^{\prime}}}{\partial r_{j}}\right)_{\text {rotation }}=-\varepsilon_{j i j^{\prime \prime}} d \varphi_{j^{\prime \prime}}=\varepsilon_{j j j^{\prime \prime}} d \varphi_{j^{\prime \prime}},\] que pueden diferir de 0. No obstante, observe que la suma de estos dos diferenciales es igual a cero para cualquiera\(d \varphi\), lo cual es posible solo si\(^{2}\)\[\left(\frac{\partial q_{j^{\prime}}}{\partial r_{j}}+\frac{\partial q_{j}}{\partial r_{j^{\prime}}}\right)_{\text {rotation }}=0, \quad \text { for } j \neq j^{\prime} .\] Es por ello que es conveniente reescribir la Eq. (5) en una forma matemáticamente equivalente,\[\left.(d l)^{2}\right|_{\text {affer deformation }}-(d l)^{2} \mid \text { |before deformation }=2 \sum_{j, j^{\prime}=1}^{3} s_{i j^{\prime}} d r_{j} d r_{j^{\prime}} \text {, }\] donde\(s_{j j}\) 'son los elementos de la llamada deformación simétrica tensor, definido como\[s_{i j^{\prime}} \equiv \frac{1}{2}\left(\frac{\partial q_{j}}{\partial r_{j^{\prime}}}+\frac{\partial q_{j^{\prime}}}{\partial r_{j}}\right) \text {. }\] (Tenga en cuenta que esta modificación no afecta a los elementos diagonales:\(s_{j j}=\partial q_{j} / \partial r_{j}\).). La ventaja del tensor simétrico\((9 \mathrm{~b})\) sobre el tensor inicial con elementos\(\partial q_{j} / \partial r_{j}\), es que de acuerdo con la Ec. (8), en rotación pura, todos los elementos del tensor de deformación simétrica desaparecen.

Ahora vamos a discutir el significado físico de este tensor. Como ya se mencionó en la Sec. 4.2, cualquier tensor simétrico puede ser diagonalizado mediante una selección apropiada de los ejes del marco de referencia. En tales ejes principales,\(s_{j j}=s_{j j} \delta_{j j}\), para que la Eq. (4) tome una forma simple:\[d q_{j}=\frac{\partial q_{j}}{\partial r_{j}} d r_{j}=s_{j j} d r_{j} .\] Podemos usar esta expresión para calcular el cambio de cada lado de un cuboide elemental (paralelepípedo) con lados\(d q_{j}\) paralelos a los ejes principales:\[\left.d r_{j}\right|_{\text {after deformation }}-\left.d r_{j}\right|_{\text {before deformation }} \equiv d q_{j}=s_{j j} d r_{j},\] y del volumen del cuboide\(d V=d r_{1} d r_{2} d r_{3}\):\[\left.d V\right|_{\text {after deformation }}-\left.d V\right|_{\text {before deformation }}=\prod_{j=1}^{3}\left(d r_{j}+s_{j j} d r_{j}\right)-\prod_{j=1}^{3} d r_{j}=d V\left[\prod_{j=1}^{3}\left(1+s_{j j}\right)-1\right]\] Desde todo nuestro análisis sólo es válido en la aproximación lineal en pequeño\(s_{j j}\), la ecuación (12) se reduce a\[\left.d V\right|_{\text {after deformation }}-\left.d V\right|_{\text {before deformation }} \approx d V \sum_{j=1}^{3} s_{j j} \equiv d V \operatorname{Tr}(\mathrm{s}),\] donde\(\operatorname{Tr}(\text { trace })^{3}\) de cualquier matriz (en particular, cualquier tensor) es la suma de sus elementos diagonales; en nuestro caso actual\(^{4}\)\[\operatorname{Tr}(\mathrm{s}) \equiv \sum_{j=1}^{3} s_{j j}\] Así, los componentes diagonales del tensor caracterizan la compresión/extensión del medio; entonces, ¿cuál es el significado de sus componentes fuera de la diagonal? Se puede ilustrar en el ejemplo más simple de deformación puramente cortante, mostrado en la Figura 2 (se supone que la geometría es uniforme a lo largo\(z\) del eje normal al plano del dibujo). En este caso, todos los desplazamientos (asumidos pequeños) tienen solo un componente cartesiano, en la Figura 2 a lo largo del\(x\) eje -:\(\mathbf{q}=\mathbf{n}_{x} \alpha y\) (con\(\alpha<1\)), de manera que el único componente distinto de cero del tensor de deformación inicial\(\partial q_{j} / \partial r_{j}\)\(\partial q_{x} / \partial y=\alpha\), es, y el tensor simétrico (\(9 \mathrm{~b}\)) es\[\mathrm{s}=\left(\begin{array}{ccc} 0 & \alpha / 2 & 0 \\ \alpha / 2 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right) .\] Evidentemente, el cambio de volumen, dado por la Eq., (13), desaparece en este caso. Así, los elementos fuera de la diagonal de los tensores caracterizan las deformaciones cortantes.

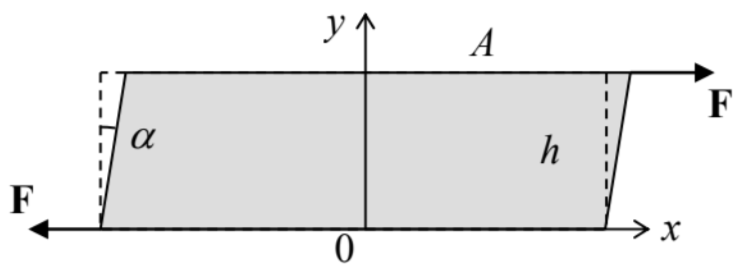Figura 7.2. Un ejemplo de cizallamiento puro.

Para concluir esta sección, permítanme señalar que la Ec. (9) sólo es válida en coordenadas cartesianas. Para la solución de algunos problemas importantes con la simetría axial o esférica, frecuentemente es conveniente expresar seis componentes diferentes del tensor de deformación simétrica a través de tres componentes del vector de desplazamiento\(\mathbf{q}\) en coordenadas cilíndricas o esféricas. Una diferenciación directa de las definiciones de estas coordenadas curvilíneas, similar a la utilizada para derivar las expresiones bien conocidas para las derivadas espaciales,\({ }^{5}\) produce, en particular, las siguientes fórmulas para los elementos diagonales del tensor:

(i) en las coordenadas cilíndricas:\[s_{\rho \rho}=\frac{\partial q_{\rho}}{\partial \rho}, \quad s_{\varphi \varphi}=\frac{1}{\rho}\left(q_{r}+\frac{\partial q_{\varphi}}{\partial \varphi}\right), \quad s_{z z}=\frac{\partial q_{z}}{\partial z} .\] (ii) en las coordenadas esféricas:\[s_{r r}=\frac{\partial q_{r}}{\partial r}, \quad s_{\theta \theta}=\frac{1}{r}\left(q_{r}+\frac{\partial q_{\theta}}{\partial \theta}\right), \quad s_{\varphi \varphi}=\frac{1}{r}\left(q_{r}+q_{\theta} \frac{\cos \theta}{\sin \theta}+\frac{1}{\sin \theta} \frac{\partial q_{\varphi}}{\partial \varphi}\right) .\] Estas expresiones, que se utilizarán a continuación para la solución de algunos problemas para geometrías simétricas, pueden ser un poco contra-intuitivas. En efecto, la Ec. (16) muestra que incluso para una deformación puramente radial, axialmentesimétrica\(\mathbf{q}=\mathbf{n}_{\rho} q(\rho)\),, la componente angular del tensor de deformación no desaparece:\(s_{\varphi \varphi}=\)\(q / \rho\). (Según la Ec. (17), en las coordenadas esféricas, ambos componentes angulares del tensor exhiben la misma propiedad). Nótese, sin embargo, que esta relación describe un efecto geométrico muy simple: el cambio de la distancia lateral\(\rho d \varphi<<\rho\) entre dos puntos cercanos con la misma distancia del eje de simetría, a un pequeño cambio de\(\rho\), que mantiene el ángulo\(d \varphi\) entre las direcciones hacia estos dos puntos constante.

---

\({ }^{1}\)Dado que ambos\(d \mathbf{q}\) y\(d \mathbf{r}\) son vectores físicos legítimos (cuyos componentes cartesianos se transforman adecuadamente como la transferencia entre marcos de referencia), la\(3 \times 3\) matriz con elementos\(\partial q_{j} / \partial r_{j}\), es de hecho un tensor físico legítimo - ver la discusión en la Sec. 4.2.

\({ }^{2}\)En consecuencia, la suma total (5), que incluye tres sumas parciales (8), no se ve afectada por la rotación -como ya sabemos.

\({ }^{3}\)La notación tradicional europea para Tr es Sp (del alemán Spur que significa “rastro” o “pista”).

\({ }^{4}\)En realidad, la teoría del tensor muestra que la traza no depende de la elección particular de los ejes de coordenadas.

\({ }^{5}\)Véase, por ejemplo, MA Eqs. (10.1) - (10.12).