8.2: Efectos de tensión superficial

Además de las fuerzas de volumen (distribuidas en volumen), una posible fuente más de presión es la tensión superficial. Este efecto es el resultado de la diferencia entre la energía potencial de las interacciones atómicas en la interfaz entre dos fluidos diferentes y la en sus volúmenes, y así puede ser descrita por una energía potencial adicional\[U_{\mathrm{i}}=\gamma A,\] donde\(A\) está el área de la interfaz, y\(\gamma\) se llama la superficie constante de tensión - o simplemente la “tensión superficial”. Para una interfaz estable de cualquiera de dos fluidos, siempre\(\gamma\) es positivo. \({ }^{8}\)Para superficies de líquidos típicos (o sus interfaces con el aire), a temperatura ambiente, la tensión superficial es igual a unos pocos\(10^{-2} \mathrm{~J} / \mathrm{m}^{2}\), correspondientes a la energía potencial\(U_{\mathrm{i}}\) de unos pocos\(10^{-2} \mathrm{eV}\) por molécula de superficie, es decir, solo una fracción de la energía de unión completa (o “cohesiva”) de la misma líquido, que suele ser del orden de\(10^{-1} \mathrm{eV}\) por molécula.

En ausencia de otras fuerzas, la tensión superficial hace que una gota de líquido sea esférica para minimizar su área superficial\(A\) a un volumen fijo. Para el análisis de los efectos de tensión superficial para geometrías más complejas, y en presencia de otras fuerzas, es conveniente reducirla a una cierta caída de presión efectiva adicional\(\Delta \mathcal{P}_{\text {ef }}\) en la interfaz. Para calcular\(\Delta \mathcal{P}_{\text {ef }}\), consideremos la condición de equilibrio de una pequeña parte\(d A\) de una interfaz suave entre dos fluidos (Figura 2), en ausencia de fuerzas a granel.

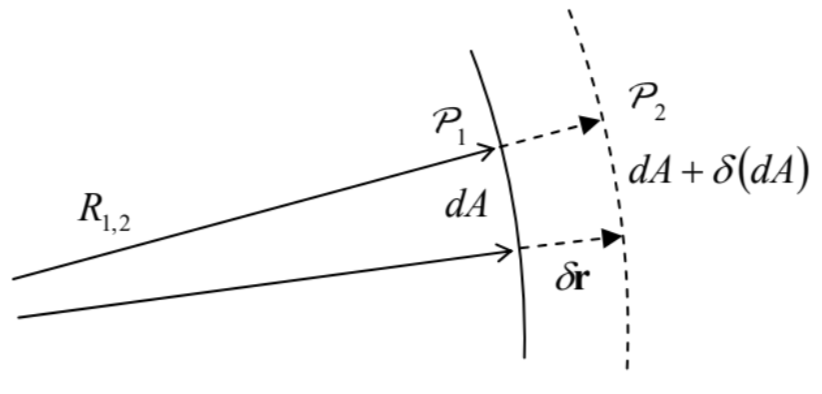Figura 8.4. Derivando la fórmula de Young-Laplace (13).

Si las presiones\(\mathcal{P}_{1,2}\) en los dos lados de la interfaz son diferentes, el trabajo de las fuerzas de tensión en el fluido 1 a un pequeño desplazamiento virtual\(\delta \mathbf{r}=\mathbf{n} \delta r\) de la interfaz (donde\(\mathbf{n}=d \mathbf{A} / d A\) está el vector unitario normal a la interfaz) es igual\[\delta \mathscr{H}=d A \delta r\left(\mathcal{P}_{1}-\mathcal{P}_{2}\right) .\] Para el equilibrio, este trabajo tiene que ser compensado por un cambio igual de la energía de la interfaz,\(\delta U_{\mathrm{i}}=\)\(\gamma \delta(d A)\). La geometría diferencial nos dice que en la aproximación lineal en\(\delta r\), el cambio relativo de la superficie elemental, correspondiente a un ángulo sólido fijo\(d \Omega\), puede expresarse como\[\frac{\delta(d A)}{d A}=\frac{\delta r}{R_{1}}+\frac{\delta r}{R_{2}},\] donde\(R_{1,2}\) están los llamados radios principales de la curvatura de la interfaz. \({ }^{10}\)Combinando Eqs. (10) - (12), obtenemos la fórmula de Young-Laplace 11\[\mathcal{P}_{1}-\mathcal{P}_{2}=\Delta \mathcal{P}_{\text {ef }} \equiv \gamma\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right) .\] En particular, esta fórmula muestra que la presión adicional creada por la tensión superficial dentro de una gota esférica de un líquido, de radio\(R\), es decir\(2 \gamma / R\), disminuye con\(R\). En contraste, según las ecuaciones (5) - (6), los efectos de las fuerzas masivas, por ejemplo la gravedad, crecen como\(\rho g R\). La comparación de estos dos componentes de presión muestra que si el radio de caída (o más generalmente, el tamaño lineal característico de una muestra de fluido) es mucho mayor que la llamada longitud capilar,\[a_{\mathrm{c}} \equiv\left(\frac{2 \gamma}{\rho g}\right)^{1 / 2}\] la tensión superficial puede ignorarse con seguridad, como se hará en todas las secciones siguientes de este capítulo, además de una breve discusión al final de la Sec. 4. Para la superficie del agua, o más exactamente su interfaz con el aire en condiciones ambientales,\(\gamma \approx 0.073 \mathrm{~J} / \mathrm{m}^{2}\) (es decir\(\mathrm{N} / \mathrm{m}\)), mientras\(\rho \approx 1,000 \mathrm{~kg} / \mathrm{m}^{3}\), para que\(a_{\mathrm{c}} \approx 4 \mathrm{~mm}\).

Por otro lado, en tubos muy estrechos, como los vasos capilares sanguíneos con radio\(a \sim 1 \mu \mathrm{m}\), es decir\(a<<a_{\mathrm{c}}\), los efectos de tensión superficial son muy importantes. La noción clave para el análisis de estos efectos es el ángulo de contacto\(\theta_{\mathrm{c}}\) (también llamado el “ángulo de humectación”) en un borde de equilibrio de un líquido humedeciendo un sólido - ver Figura 5.

Figura 8.5. Ángulos de contacto para (a) superficies hidrófilas y (b) hidrófobas.

Según su definición (10), la constante\(\gamma\) puede interpretarse como una fuerza (por unidad de longitud del límite de la interfaz) dirigida normalmente al límite, y “tratando” de reducir el área de la interfaz. Como resultado, el balance de componentes horizontales de las tres fuerzas de este tipo, mostrado en la Figura 5a, produce inmediatamente la ecuación de Young\[\gamma_{\mathrm{sl}}+\gamma_{\mathrm{lg}} \cos \theta_{\mathrm{c}}=\gamma_{\mathrm{sg}},\] donde los índices de constantes\(\gamma\) corresponden a tres posibles interfaces entre el líquido, el sólido y el gas. Para las llamadas superficies hidrofílicas a las que “les gusta estar mojadas” por un líquido en particular (no necesariamente agua), lo que significa que\(\gamma_{\mathrm{sl}}<\gamma_{\mathrm{sg}}\), esta relación rinde\(\cos \theta_{\mathrm{c}}>0\), es decir,\(\theta_{\mathrm{c}}<\pi / 2-\) la situación que se muestra en la Figura 5a. Por otro lado, para superficies hidrófobas con\(\gamma_{\mathrm{sl}}>\gamma_{\mathrm{sg}}\), la Ec. (15) produce ángulos de contacto más grandes,\(\theta_{\mathrm{c}}>\pi / 2\) - ver Figura\(5 b\).

Utilicemos esta noción para resolver el problema más simple y quizás el más importante prácticamente de este campo: encontrar la altura\(h\) de la columna de fluido levantada por las fuerzas de tensión superficial en un tubo vertical estrecho hecho de un material hidrófilo, asumiendo que su superficie interna es un cilindro redondo de radio\(a\) - ver Figura 6. Dentro de un fluido incompresible, la presión cae con la altura según la ecuación de Pascal (6), de manera que justo debajo de la superficie,\(\mathcal{P} \approx \mathcal{P}_{0}-\rho g h\), donde\(\mathcal{P}_{0}\) está la presión de fondo (e.g., atmosférica). Esto significa que a\(a<<h\) la variación de presión a lo largo de la superficie cóncava (llamada menisco) del líquido es insignificante, de manera que según la ecuación de Young-Poisson (13), la suma\(\left(1 / R_{1}+1 / R_{2}\right)\) tiene que ser virtualmente constante a lo largo de la superficie. Debido a la simetría axial del problema, esto significa que la superficie tiene que ser parte de una esfera. A partir de la definición del ángulo de contacto, el radio\(R\) de la esfera es igual para\(a / \cos \theta_{\mathrm{c}}-\) ver Figura 6. Conectando esta relación en la Ec. (3) con\(\mathcal{P}_{1}-\mathcal{P}_{2}=\rho g h\), obtenemos el siguiente resultado para\(h\):\[\rho g h=\frac{2 \gamma \cos \theta_{\mathrm{c}}}{a} .\] En retrospectiva, este resultado podría obtenerse más directamente, al requerir que el peso total\(\rho g V=\)\(\rho g\left(\pi a^{2} h\right)\) de la columna del líquido levantado sea igual al componente vertical\(F \cos \theta_{\mathrm{c}}\) de la fuerza de tensión superficial completa\(F=p p\), actuando sobre el perímetro\(p=2 \pi a\) del menisco. Usando la definición (11) de la longitud capilar\(a_{\mathrm{c}}\), la ecuación (16a) puede representarse como la llamada regla Jurin:\[h=\frac{a_{\mathrm{c}}^{2}}{a} \cos \theta_{\mathrm{c}} \leq \frac{a_{\mathrm{c}}^{2}}{a}\] según nuestra suposición inicial\(h>>a\), la ecuación (16) solo es válida para tubos estrechos, con radio\(a<<a_{\mathrm{c}}\).

Figura 8.6. Subida de líquido en un tubo capilar vertical.

Esta elevación capilar es el mecanismo básico para elevar el agua con nutrientes desde las raíces hasta las ramas y hojas de las plantas, de manera que las alturas de los árboles más altas corresponden a la regla de Jurin (16)\(\cos \theta_{c}\)\(\approx 1\), con, y el radio de poro\(a\) limitado desde abajo por unas pocas micras, debido a la efectos de viscosidad que restringen la descarga de fluido - ver Sec. 5 a continuación.

---

\({ }^{8}\)De hecho, si el\(\gamma\) de la interfaz de ciertos dos fluidos es negativo, se autoreconfigura para disminuir\(U_{\mathrm{i}}\), es decir, aumentar\(\left|U_{\mathrm{i}}\right|\), al aumentar el área de la interfaz, es decir, fragmenta el sistema en una solución macroscópicamente uniforme.

\({ }^{9}\)Esta igualdad se deriva de la relación general (7.30), con los elementos tensores de tensión expresados por la Ec. (2), pero en este simple caso de la fuerza de tensión neta\(d \mathbf{F}=\left(\mathcal{P}_{1}-\mathcal{P}_{2}\right) d \mathbf{A}\) paralela al vector del elemento de interfaz\(d \mathbf{A}\), puede obtenerse aún más simplemente solo de la definición de trabajo: \(\delta \mathscr{W}=d \mathbf{F} \cdot \delta \mathbf{r}\)en el desplazamiento virtual\(\delta \mathbf{r}=\mathbf{n} \delta r\).

\({ }^{10}\)Esta fórmula general puede verificarse por medios elementales para una esfera de radio\(r\) (para la cual\(R_{1}=R_{2}=r\) y\(d A=r^{2} d \Omega\), para que\(\delta(d A) / d A=\delta\left(r^{2}\right) / r^{2}=2 \delta r / r\)), y para una interfaz cilíndrica redonda de radio\(R\) (para la cual\(R_{1}=r\),\(R_{2}=\infty\), y\(d A=r d \varphi d z\), para que\(\left.\delta(d A) / d A=\delta r / r\right)\). Para más información sobre curvatura, véase, por ejemplo, M. do Camo, Geometría diferencial de curvas y superficies,\(2^{\text {nd }}\) ed., Dover,\(2016 .\)

\({ }^{11}\)Este resultado (que no debe confundirse con la ecuación (15), llamada ecuación de Young) fue derivado en 1806 por Pierre-Simon Laplace (de la fama de operador/ecuación de Laplace) sobre la base del primer análisis de los efectos de tensión superficial de Thomas Young (sí, el mismo Young que interpretó el famoso ¡Experimenta con la luz!) un año antes.