9.1: Caos en los mapas

La posibilidad de dinámicas cuasi-aleatorias de sistemas deterministas con unos pocos grados de libertad (hoy en día llamado el caos determinista -o simplemente “caos”) se había notado antes del\(20^{\text {th }}\) siglo,\({ }^{1}\) pero se ha reconocido ampliamente solo después de la publicación de un artículo de 1963 por teórica meteorólogo Edward Lorenz. En ese trabajo, examinó soluciones numéricas del siguiente sistema de tres ecuaciones diferenciales ordinarias no lineales,\[\begin{aligned} \dot{q}_{1} &=a_{1}\left(q_{2}-q_{1}\right) \\ \dot{q}_{2} &=a_{2} q_{1}-q_{2}-q_{1} q_{3}, \\ \dot{q}_{3} &=q_{1} q_{2}-a_{3} q_{3}, \end{aligned}\] como modelo rudimentario de transferencia de calor a través de una capa horizontal de fluido que separa dos placas sólidas. (El experimento muestra que si la placa inferior se mantiene más caliente que la superior, el líquido puede exhibir convección turbulenta). Ha encontrado que dentro de cierto rango de las constantes\(a_{1,2,3}\), la solución a la ecuación (1) sigue trayectorias complejas, impredecibles y no repetitivas en el\(q\) espacio 3D. Además, las funciones\(q_{j}(t)\) (donde\(j=1,2,3\)) son tan sensibles a las condiciones iniciales\(q_{j}(0)\) que en tiempos suficientemente grandes\(t\), las soluciones correspondientes a condiciones iniciales ligeramente diferentes se vuelven completamente diferentes.

Muy pronto se dio cuenta de que tal comportamiento es típico de objetos matemáticos aún más simples llamados mapas para que inicie mi discusión sobre el caos a partir de estos objetos. Un mapa 1D es esencialmente una regla para encontrar el siguiente número\(q_{n+1}\) de una secuencia discreta numerada por el índice entero\(n\), en los casos más simples usando solo su último valor conocido\(q_{n}\). El ejemplo más famoso es el llamado\(\operatorname{logistic}\) mapa:\(^{2}\)\[q_{n+1}=f\left(q_{n}\right) \equiv r q_{n}\left(1-q_{n}\right) .\] Las propiedades básicas de este mapa pueden entenderse utilizando la representación gráfica (ojalá, autoexplicativa) que se muestra en la Figura 1. \({ }^{3}\)Se puede ver fácilmente que en\(r<1\) (Figura 1a) la secuencia del mapa logístico converge rápidamente al punto fijo trivial\(q^{(0)}=0\), ya que cada valor siguiente de\(q\) es menor que el anterior. Sin embargo, si\(r\) se incrementa por encima de 1 (como en el ejemplo mostrado en la Figura 1b), el punto fijo\(q^{(0)}\) se vuelve inestable. En efecto, at\(q_{n}<<1\), el mapa rinde\(q_{n+1} \approx r q_{n}\), de modo que at\(r>1\), los valores\(q_{n}\) crecen con cada iteración. En lugar del punto inestable\(q^{(0)}=0\), en el rango\(1<r<r_{1}\), donde\(r_{1} \equiv 3\), el mapa tiene un punto fijo estable\(q^{(1)}\) que se puede encontrar al enchufar este valor en ambas partes de la Ec. (2):\[q^{(1)}=f\left(q^{(1)}\right) \equiv r q^{(1)}\left(1-q^{(1)}\right),\] dando\(q^{(1)}=1-1 / r-\) ver la rama izquierda de la gráfica que se muestra en la Figura\(2 .\)

Figura 9.1. Análisis gráfico del mapa logístico para: (a)\(r<1\) y (b)\(r>1\).

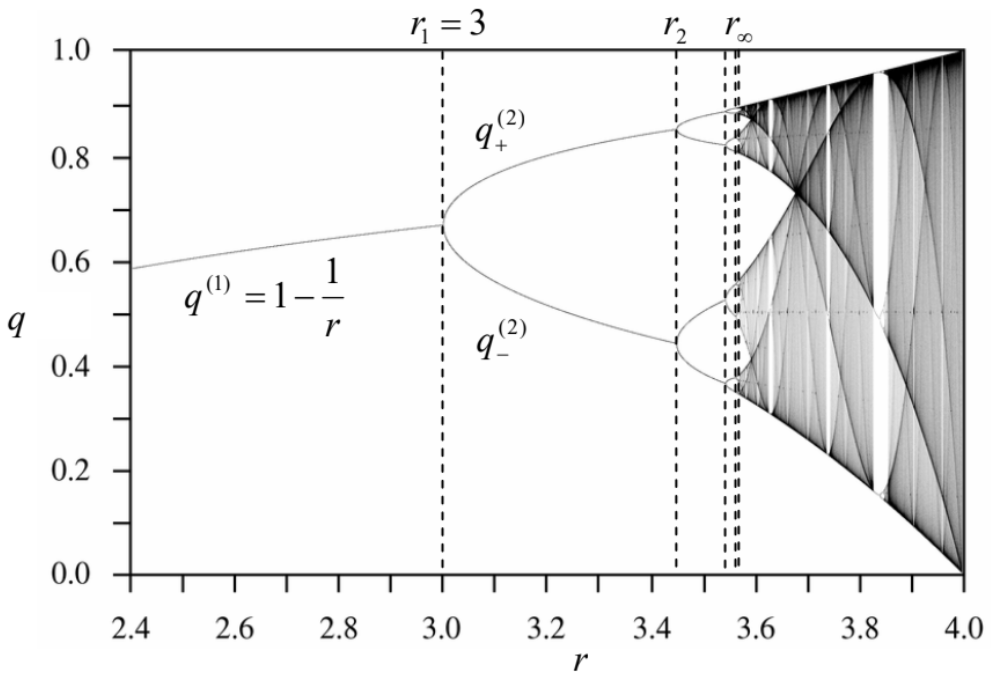Figura 9.2. Los puntos fijos y regiones caóticas del mapa logístico. Adaptado, bajo el CCO 1.0 Universal Public Domain Dedication, del original de Jordan Pierce, disponible en http://en.wikipedia.org/wiki/Logistic_map. (Una simulación en vivo muy agradable del mapa también está disponible en este sitio web.)

Sin embargo, en\(r>r_{1}=3\), el punto fijo\(q^{(1)}\) también se vuelve inestable. Para probarlo, tomemos
\(q_{n} \equiv q^{(1)}+\widetilde{q}_{n}\), supongamos que la desviación\(\widetilde{q}_{n}\) del punto fijo\(q^{(1)}\) es pequeña, y linealizar el mapa (2)
en tal como\(\widetilde{q}_{n}-\) lo hicimos repetidamente para las ecuaciones diferenciales anteriormente en este curso. El resultado es\[\widetilde{q}_{n+1}=\left.\frac{d f}{d q}\right|_{q=q^{(1)}} \widetilde{q}_{n}=r\left(1-2 q^{(1)}\right) \widetilde{q}_{n}=(2-r) \widetilde{q}_{n} .\] Para probar eso, tomemos\[\widetilde{q}_{n+1}=\left.\frac{d f}{d q}\right|_{q=q^{(1)}} \tilde{q}_{n}=r\left(1-2 q^{(1)}\right) \widetilde{q}_{n}=(2-r) \widetilde{q}_{n} .\] Muestra que al\(0<2-r<1\), es decir, a\(1<r<2\), las desviaciones\(\widetilde{q}_{n}\) disminuyen monótonamente. At\(-1<2-r\)\(<0\), es decir, en el rango\(2<r<3\), el signo de las desviaciones alterna, pero su magnitud aún disminuye\(-\) como en un foco estable, ver Sec. 5.6. Sin embargo, en\(-1<2-r\), es decir\(r>r_{1} \equiv 3\), las desviaciones crecen por magnitud, sin dejar de cambiar su signo, en cada paso. Dado que la Ec. (2) no tiene otros puntos fijos, esto significa que at\(n\)\(\rightarrow \infty\), los valores\(q_{n}\) no convergen a un punto; más bien, dentro del rango\(r_{1}<r<r_{2}\), se acercan a un ciclo límite de alternancia de dos puntos,\(q_{+}{ }^{(2)}\) y\(q_{-}{ }^{(2)}\), que satisfacen el siguiente sistema de Ecuaciones algebraicas:\[q_{+}^{(2)}=f\left(q_{-}^{(2)}\right), \quad q_{-}^{(2)}=f\left(q_{+}^{(2)}\right) .\] Estos puntos también se trazan en la Figura 2, como funciones del parámetro\(r\). Lo que ha ocurrido en ese punto\(r_{1}\)\(=3\) se llama bifurcación de duplicación de período.

La historia se repite en\(r=r_{2} \equiv 1+\sqrt{6} \approx 3.45\), donde el sistema pasa del ciclo límite de 2 puntos a un ciclo de 4 puntos, luego en\(r=r_{3} \approx 3.54\), donde el ciclo límite se vuelve consistente en 8 puntos alternos, etc. Lo más destacable, los puntos de bifurcación de duplicación de período\(r_{n}\), en que el número de puntos en el ciclo límite duplica de\(2^{n-1}\) puntos a\(2^{n}\) puntos, se vuelven cada vez más cercanos. Los cálculos numéricos muestran que en\(n \rightarrow \infty\), estos puntos obedecen al siguiente comportamiento asintótico:\[r_{n} \rightarrow r_{\infty}-\frac{C}{\delta^{n}}, \text { where } r_{\infty}=3.5699 \ldots, \quad \delta=4.6692 \ldots\] El parámetro\(\delta\) se llama la constante Feigenbaum; para otros mapas, y algunos sistemas dinámicos (ver la siguiente sección), las secuencias de duplicación de períodos siguen una ley similar, pero con valores diferentes de\(\delta\).

Más importante para nosotros, sin embargo, es lo que sucede en\(r>r_{\infty} .\) Numerosos experimentos numéricos, repetidos con precisión creciente,\({ }^{4}\) han confirmado que aquí el sistema está completamente desordenado, sin ciclo límite reproducible, aunque (como muestra la Figura 2) en\(r \approx r_{\infty}\), todos los valores secuenciales\(q_{n}\) son todavía confinados a unas pocas regiones estrechas. \({ }^{5}\)Sin embargo, a medida\(r\) que el parámetro se incrementa mucho más allá\(r_{\infty}\), estas regiones se amplían y fusionan. Este es el llamado caos profundo, sin ningún orden aparente en absoluto. \({ }^{6}\)

La característica más importante del caos (en este y en cualquier otro sistema) es la divergencia exponencial de trayectorias. Para un mapa 1D, esto significa que aunque las condiciones iniciales\(q_{1}\) en dos implementaciones de mapas difieran en una cantidad muy pequeña\(\Delta q_{1}\), la diferencia\(\Delta q_{n}\) entre las secuencias correspondientes\(q_{n}\) está creciendo, en promedio, exponencialmente con\(n\). Dichos exponentes pueden ser utilizados para caracterizar el caos. En efecto, una generalización evidente de la Ec. (4) a un punto arbitrario\(q_{n}\) es\[\Delta q_{n+1}=e_{n} \Delta q_{n},\left.\quad e_{n} \equiv \frac{d f}{d q}\right|_{q=q_{n}} .\] Supongamos que\(\Delta q_{1}\) es tan pequeño que los\(N\) primeros valores\(q_{n}\) están relativamente cerca unos de otros. Luego usando la Ec. (7) iterativamente para estos pasos, obtenemos Los experimentos\[\Delta q_{N}=\Delta q_{1} \prod_{n=1}^{N} e_{n}, \quad \text { so that } \ln \left|\frac{\Delta q_{N}}{\Delta q_{1}}\right|=\sum_{n=1}^{N} \ln \left|e_{n}\right| \text {. }\] numéricos muestran que en la mayoría de los regímenes caóticos, a\(N \rightarrow \infty\) tal suma fluctúa alrededor de un promedio, que crece a medida que\(\lambda N\), con el parámetro\[\lambda \equiv \lim _{\Delta q_{1} \rightarrow 0} \lim _{N \rightarrow \infty} \frac{1}{N} \sum_{n=1}^{N} \ln \left|e_{n}\right|,\] llamado el exponente Lyapunov\({ }^{7}\) siendo independiente de la condiciones iniciales. El panel inferior de la Figura 3 muestra\(\lambda\) como función del parámetro\(r\) para el mapa logístico (2). (Su panel superior muestra los mismos datos que la Figura 2, y se reproduce aquí solo por el bien de la comparación.)

Figura 9.3. El exponente de Lyapunov para el mapa logístico. Adaptado, con permiso, de la monografía de Schuster y Just (citada a continuación). C Wiley-VCH Verlag\(\mathrm{GmbH}\) & Co. KGaA.

Obsérvese que at\(r<r_{\infty}, \lambda\) es negativo, indicando la estabilidad de la secuencia, además de los puntos\(r_{1}, r_{2}, \ldots\) donde se\(\lambda\) volverían positivos si los cambios del ciclo límite (bifurcaciones) no la hubieran devuelto al territorio negativo. Sin embargo, at\(r>r_{\infty}, \lambda\) se vuelve positivo, volviendo a valores negativos solo en intervalos limitados de ciclos límite estables. Es evidente que en experimentos numéricos (que dominan los estudios del caos determinista) el exponente Lyapunov puede ser utilizado como una buena medida de la profundidad del caos. \({ }^{8}\)

A pesar de toda la abundancia de resultados publicados para mapas particulares,\({ }^{9}\) y de varias observaciones generales interesantes (como la existencia de las secuencias de bifurcación de Feigenbaum), hasta donde yo sé, nadie puede predecir los patrones como los que se muestran en las figuras 2 y 3 con solo mirar el regla de mapeo en sí, es decir, sin llevar a cabo experimentos numéricos reales. Desafortunadamente, la comprensión del caos determinista en otros sistemas no es mucho mejor.

---

\({ }^{1}\)Se remonta al menos a un trabajo de 1892 del mismo Jules Henri Poincaré que ya fue mencionado con reverencia en el Capítulo 5. Citándolo: “... puede suceder que pequeñas diferencias en las condiciones iniciales produzcan unas muy grandes en los fenómenos finales. [...] La predicción se vuelve imposible”.

\({ }_{2}\)Sus propiedades caóticas fueron discutidas por primera vez en 1976 por Robert May, aunque el mapa en sí es uno de los modelos ecológicos simples discutidos repetidamente mucho antes, y puede remontarse al menos a la obra de 1838 de Pierre François Verhulst.

\({ }^{3}\)Dado que el valor máximo de la función\(f(q)\), alcanzado en\(q=1 / 2\)\(r / 4\), es igual, el mapeo puede limitarse al segmento\(x=[0,1]\), si el parámetro\(r\) está entre 0 y 4. Dado que todas las propiedades interesantes del mapa, incluido el caos, se pueden encontrar dentro de estos límites, voy a discutir sólo esta gama de\(r\).

\({ }^{4}\)El lector debe recordar que al igual que los experimentos habituales (“naturaleza”), los experimentos numéricos también tienen una precisión limitada, debido a errores inevitables de redondeo.

\({ }^{5}\)La geometría de estas regiones es esencialmente fractal, es decir, tiene una dimensionalidad intermedia entre 0 (que cualquier conjunto final de puntos geométricos tendría) y 1 (pertinente a un continuo 1D). Se puede encontrar una extensa discusión sobre las geometrías fractales y su relación con el caos determinista, por ejemplo, en el libro de B. Mandelbrot, The Fractal Geometry of Nature, W. H. Freeman,\(1983 .\)

\({ }^{6}\)Esto no quiere decir que el desarrollo de los caos sea siempre una función monótona de\(r\). Como muestra la Figura 2, dentro de ciertos intervalos de este parámetro, el comportamiento caótico desaparece repentinamente, siendo reemplazado, típicamente, por un ciclo límite de pocos puntos, solo para reanudarse en el otro lado del intervalo. A veces (¡pero no siempre!) la “ruta al caos” en los límites de estos intervalos sigue la misma secuencia de bifurcaciones de duplicación de períodos de Feigenbaum.

\({ }^{7}\)Después de Alexandr Mikhailovich Lyapunov (1857-1918), famoso por sus estudios de la estabilidad de los sistemas dinámicos.

\({ }^{8} N\)-mapas dimensionales que relacionan vectores\(N\) -dimensionales en lugar de escalares, pueden caracterizarse por exponentes de\(N\) Lyapunov en lugar de uno. Para un comportamiento caótico, es suficiente que solo uno de ellos se vuelva positivo. Para tales sistemas, otra medida del caos, la entropía de Kolmogorov, puede ser más relevante. Esta medida, y su relación con los exponentes de Lyapunov, se discuten, por ejemplo, en SM Sec. \(2.2\).

\({ }^{9}\)Véase, por ejemplo, los Capítulos 2-4 en H. Schuster y W. Just, Deterministic Chaos,\(4^{\text {th }}\) ed., Wiley-VCH, 2005, o Capítulos 8-9 en J. Thompson y H. Stewart, Nonlinear Dynamics and Chaos,\(2^{\text {nd }}\) ed., Wiley, 2002.