25.1: Ejemplos de Momentos de Inercia

Moléculas

El momento de inercia de la molécula de hidrógeno fue históricamente importante. Es trivial de encontrar: los núcleos (protones) tienen el 99.95% de la masa, por lo que da una imagen clásica de dos masas puntuales a\(m\) una distancia fija de\(a\) distancia\(I=\frac{1}{2} m a^{2}\). En el siglo XIX, el misterio era que la equipartición de energía, que daba una excelente cuenta de los calores específicos de casi todos los gases, no funcionaba para el hidrógeno —a bajas temperaturas, aparentemente estas moléculas diatómicas no giraban alrededor, a pesar de que chocaron constantemente entre sí. La resolución fue que el momento de inercia era tan bajo que se necesitaba mucha energía para excitar el primer estado de momento angular cuantificado,\(L=\hbar\) Este no fue el caso de los gases diatómicos más pesados, ya que la energía del estado de momento angular más bajo\(E=L^{2} / 2 I=\hbar^{2} / 2 I\), es menor para las moléculas con momentos más grandes de inercia.

Aquí hay una molécula plana simple:

Obviamente, un eje principal es a través del centroide, perpendicular al plano. También hemos establecido que cualquier eje de simetría es un eje principal, por lo que evidentemente hay tres ejes principales en el plano, ¡uno a lo largo de cada enlace! La única interpretación es que hay una degeneración: hay dos ejes principales de igual valor en el plano, y cualesquiera dos ejes perpendiculares estarán bien. El momento de inercia alrededor de cualquiera de estos ejes será la mitad que alrededor del eje perpendicular al plano.

¿Qué pasa con una molécula tridimensional simétrica?

Aquí tenemos cuatro ejes principales obvios: solo es posible si tenemos degeneración esférica, es decir, los tres ejes principales tienen el mismo momento de inercia.

Varias Formas

Una varilla delgada, densidad de masa lineal\(\lambda\), longitud\(ℓ\):

\ begin {ecuación}
I=2\ int_ {0} ^ {\ ell/2}\ lambda x^ {2} d x=2\ lambda\ ell^ {3}/24=\ frac {1} {12} m\ ell^ {2}
\ end {ecuación}

Un cuadrado de masa\(m\), lateral\(ℓ\), alrededor de un eje en su plano, a través del centro, perpendicular a un lado:

\ begin {ecuación}
I=\ frac {1} {12} m\ ell^ {2}
\ end {ecuación}

(Es sólo una fila de varillas.) de hecho, el momento es el mismo respecto a cualquier línea del plano a través del centro, desde la simetría, y el momento alrededor de una línea perpendicular al plano a través del centro es el doble de esto—esa fórmula dará entonces el momento de inercia de un cubo, alrededor de cualquier eje a través de su centro.

Un disco de masa\(M\), radio\(a\) y densidad superficial\(\sigma\) tiene

\ begin {ecuación}
I=\ int_ {0} ^ {a} r^ {2}\ cdot\ sigma\ cdot 2\ pi r d r=\ frac {1} {2}\ pi a^ {4}\ sigma=\ frac {1} {2} M a^ {2}
\ fin {ecuación}

Esto también es correcto para un cilindro (pensarlo como una pila de discos) alrededor de su eje.

Un disco alrededor de una línea a través de su centro en su plano debe ser\(\frac{1}{4} M a^{2}\) del teorema del eje perpendicular. Un cilindro sólido alrededor de una línea a través de su centro perpendicular a su eje principal puede considerarse como una pila de discos, de radio\(a\), altura\(h\), tomando la masa de un disco como\(\rho d z\) y utilizando el teorema de ejes paralelos,

\ begin {ecuación}
I=2\ int_ {0} ^ {h/2}\ rho d z\ izquierda (\ frac {1} {4} a^ {2} +z^ {2}\ derecha) =\ frac {1} {4} M a^ {2} +\ frac {1} {12} M h^ {2}
\ end {ecuación}

Para una esfera, una pila de discos de radios variables,

\ begin {ecuación}
I=\ int_ {-a} ^ {a} d z\ frac {1} {2}\ rho\ pi\ left (a^ {2} -z^ {2}\ derecha) ^ {2} =\ frac {8} {15}\ rho\ pi a^ {5} =\ frac {2} {5} M a^ {2}
\ terminar ecuación}

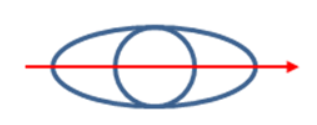
Un elipsoide de revolución y una esfera de la misma masa y radio tienen claramente el mismo movimiento de inercia alrededor de su eje común (mostrado).

Momentos de inercia de un cono

Siguiendo a Landau, tomamos altura\(h\) y radio base\(R\) y ángulo semivertical\(\alpha\) para que\(R=h \tan \alpha\).

Como preliminar, el volumen del cono es

\(V=\int_{0}^{h} \pi r^{2} d z=\int_{0}^{h} \pi\left(\frac{R z}{h}\right)^{2} d z=\frac{1}{3} \pi R^{2} h\)

El centro de masa es la\(a\) distancia del vértice, donde

\ begin {ecuación}
a v=a\ cdot\ frac {1} {3}\ pi R^ {2} h=\ int_ {0} ^ {h} z d V=\ int_ {0} ^ {h}\ pi z\ izquierda (\ frac {R z} {h}\ derecha) ^ {2} d z=\ frac {1} {4}\ pi R^ {2} h^ {2},\ quad a=\ frac {3} {4} h
\ final {ecuación}

El momento de inercia alrededor del eje central del cono es (tomando densidad\(\rho\)) el de una pila de discos cada uno con masa

\ begin {ecuación}
m (d z) =\ pi r^ {2}\ rho d z=\ pi\ izquierda (\ frac {R z} {h}\ derecha) ^ {2}\ rho d z
\ fin {ecuación}

y momento de inercia\(I(d z)=\frac{1}{2} m(d z) r^{2}\)

\ begin {ecuación}
\ int_ {0} ^ {h}\ frac {1} {2}\ pi\ rho\ izquierda (\ frac {R z} {h}\ derecha) ^ {4} d z=\ frac {1} {10}\ pi\ rho R^ {4} h=\ frac {3} {10} M R^ {2}
\ end {ecuación}

El momento de inercia alrededor del eje\(x_{1}^{\prime}\) a través del vértice, perpendicular al eje central, se puede calcular utilizando el enfoque de eje paralelo de pila de discos, teniendo los discos masa\(\pi \rho\left(\frac{R z}{h}\right)^{2} d z\), es

\ begin {ecuación}
\ int_ {0} ^ {h}\ pi\ rho\ izquierda (\ frac {R z} {h}\ derecha) ^ {2}\ izquierda [\ frac {1} {4}\ izquierda (\ frac {R z} {h}\ derecha) ^ {2} +z^ {2}\ derecha] d z=\ frac {1} {20} pi\ rho R^ {4} h+\ frac {1} {5}\ pi\ rho R^ {2} h^ {3} =\ frac {3} {20} M R^ {2} +\ frac {3} {5} M h^ {2}
\ end {ecuación}