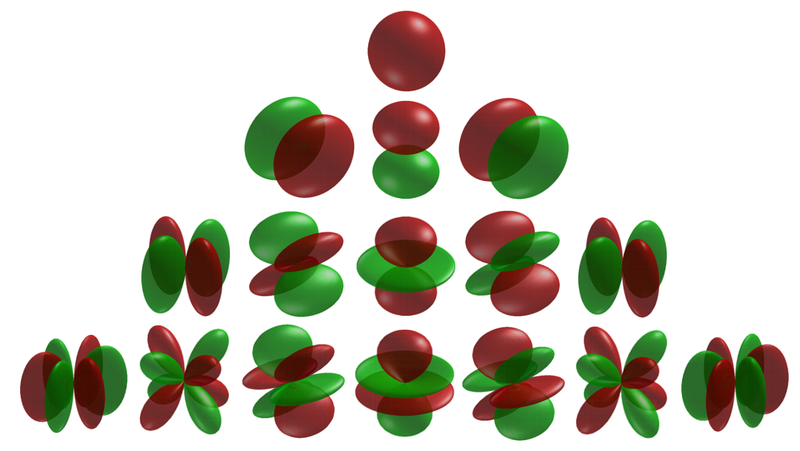
3: Momento angular en mecánica cuántica

Objetivos

En este capítulo discutimos el operador de momento angular, uno de varios operadores relacionados, análogo al momento angular clásico. El operador de momento angular juega un papel central en la teoría de la física atómica y otros problemas cuánticos que involucran la simetría rotacional. Tanto en los sistemas mecánicos clásicos como cuánticos, el momento angular (junto con el impulso lineal y la energía) es una de las tres propiedades fundamentales del movimiento.

Prerrequisitos

Capítulos 1 y 2. Momento angular y su conservación en mecánica clásica. Coordenadas esféricas, elementos de análisis vectorial. Ecuación de Laplace.

Ecuación de autovalor en coordenadas polares

La definición clásica del vector de momento angular es

\(\mathcal{L}=\mathbf{r} \times \mathbf{p}\)(3.1)

que depende de la elección del punto de origen donde | r |=r=0|r|=r=0. Con la definición de la posición y los operadores de momento obtenemos el operador de momento angular como

\(\hat{\mathbf{L}}=-i \hbar(\mathbf{r} \times \nabla)\)(3.2)

Los componentes cartesianos de\(\hat{\mathbf{L}}\) son entonces

\(\hat{L}_{x}=-i \hbar\left(y \partial_{z}-z \partial_{y}\right), \quad \hat{L}_{y}=-i \hbar\left(z \partial_{x}-x \partial_{z}\right), \quad \hat{L}_{z}=-i \hbar\left(x \partial_{y}-y \partial_{x}\right)\)(3.3)

Con frecuencia se necesitan los componentes de\(\hat{\mathbf{L}}\) en coordenadas esféricas. Para obtenerlos tenemos que hacer uso de la expresión del vector de posición por coordenadas esféricas, las cuales están conectadas a los componentes cartesianos mediante

\(\mathbf{r}=x \hat{\mathbf{e}}_{x}+y \hat{\mathbf{e}}_{y}+z \hat{\mathbf{e}}_{z}=r \sin \theta \cos \phi \hat{\mathbf{e}}_{x}+r \sin \theta \sin \phi \hat{\mathbf{e}}_{y}+r \cos \theta \hat{\mathbf{e}}_{z}\)(3.4)

Pasando a los componentes esféricos en (3.3), y usando la regla de cadena:

\(\partial_{x}=\left(\partial_{x} r\right) \partial_{r}+\left(\partial_{x} \theta\right) \partial_{\theta}+\left(\partial_{x} \phi\right) \partial_{\phi}\)(3.5)

y de manera similar para\(∂y\) y\(∂z\) da los siguientes componentes

\ (\ begin {alineado}
&\ hat {L} _ _ {x} =i\ hbar\ izquierda (\ sin\ phi\ parcial_ {\ theta} +\ cot\ theta\ cos\ phi\ parcial_ {\ phi}\ derecha)\\
&\ hat {L} _ _ {y} =i\ hbar\ izquierda (-\ cos\ phi\ parcial_ {\ theta} +\ cuna\ theta\ sin\ phi\ parcial_ {\ phi}\ derecha)\\
&\ sombrero {L} _ {z} =-i\ hbar\ parcial_ {\ phi}
\ end {alineado}\) (3.6)

Se ve a la vez la razón y la ventaja de usar coordenadas esféricas: los operadores en cuestión no dependen de la variable radial r. Esto por supuesto también es cierto para\(\hat{L}^{2}=\hat{L}_{x}^{2}+\hat{L}_{y}^{2}+\hat{L}_{z}^{2}\) lo que resulta ser\(−ℏ^{2}\) veces la parte angular del operador de Laplace\(Δ_{θϕ}\).

\(\hat{L}^{2}=-\hbar^{2}\left(\partial_{\theta \theta}^{2}+\cot \theta \partial_{\theta}+\frac{1}{\sin ^{2} \theta} \partial_{\phi \phi}^{2}\right)=-\hbar^{2} \Delta_{\theta \phi}\)(3.7)

Ahora encontraremos las funciones propias de\(Δ_{θϕ}\), que juegan un papel muy importante en la mecánica cuántica, y de hecho en varias ramas de la física teórica. Serán funciones de\(0 \leq \theta \leq \pi\) y\(0 \leq \phi<2 \pi\), es decir, pueden considerarse como funciones complejas de valor cuyo dominio es la esfera unitaria. Las funciones propias de se\(\hat{L}^{2}\) denotarán por\(Y(θ,ϕ)\), y la ecuación angular del valor propio es:

\ (\ begin {alineado}
-\ Delta_ {\ theta\ phi} Y (\ theta,\ phi) &=\ ell (\ ell+1) Y (\ theta,\ phi)\ quad\ text {o}\\
\ izquierda (\ parcial_ {\ theta\ theta} ^ {2} +\ cot\ theta\ parcial_ {\ theta} +\ frac 1} {\ sin ^ {2}\ theta}\ parcial_ {\ phi\ phi} ^ {2}\ derecha) Y (\ theta,\ phi) &=-\ ell (\ ell+1) Y (\ theta,\ phi)
\ end {alineado}\) (3.8)

Uno podría preguntarse cuál es la razón para escribir el valor propio en la forma\(ℓ(ℓ+1)\), pero como resultará pronto, no hay pérdida de generalidad en esta notación.

Separación de la ecuación del valor propio

Intentamos la separación de las variables:

\(Y(\theta, \phi)=\Theta(\theta) \Phi(\phi)\)(3.9)

Conectando esto en (3.8) y dividiendo por\(ΘΦ\), encontramos

\(\left\{\frac{1}{\Theta}\left[\sin \theta \frac{d}{d \theta}\left(\sin \theta \frac{d \Theta}{d \theta}\right)\right]+\ell(\ell+1) \sin ^{2} \theta\right\}+\frac{1}{\Phi} \frac{d^{2} \Phi}{d \phi^{2}}=0\)(3.10)

El primer término depende sólo de\(θ\) mientras que el último es una función de sólo\(ϕ\). Para satisfacer esta ecuación para todos los valores de\(θ\) y\(ϕ\) estos términos deben ser por separado iguales a una constante con signos opuestos. Esta constante se denota tradicionalmente por\(m^{2}\) y\(−m^{2}\) (tenga en cuenta que esta no es la masa) y tenemos dos ecuaciones: una para\(Θ\), y otra para\(Φ\). Consideramos el segundo, y tenemos:

\(\frac{1}{\Phi} \frac{d^{2} \Phi}{d \phi^{2}}=-m^{2}\)(3.11)

Dos soluciones linealmente independientes son

\ (\ Phi (\ phi) =\ left\ {\ begin {array} {l}
e^ {i m\ phi}\\
e^ {-i m\ phi}
\ end {array}\ derecha.\) (3.12)

y cualquier combinación lineal de ellos. Uno puede elegir\(e^{imϕ}\), e incluir el otro permitiendo que mm sea negativo. Al tratarse de funciones de puntos en el espacio real tridimensional, los valores de\(Φ(ϕ)\) y\(Φ(ϕ+2π)\) deben ser los mismos, ya que estos valores del argumento corresponden a puntos idénticos en el espacio. Entonces\(e^{im(ϕ+2π)}=e^{imϕ}\), y\(e^{im2π}=1\) hay que aguantar. De esto se deduce que mm debe ser un entero

\(\Phi(\phi)=\frac{1}{\sqrt{2 \pi}} e^{i m \phi} \quad m=0, \pm 1, \pm 2 \ldots\)(3.15)

Aquí se\(\frac{1}{\sqrt{2 \pi}}\) ha elegido la constante de integración para que ya\(Φ(ϕ)\) se normalice a la unidad al momento de integrar con respecto a\(ϕ\) de 0 a\(2π\).

La ecuación para\(Θ\)

\(\sin \theta \frac{d}{d \theta}\left(\sin \theta \frac{d \Theta}{d \theta}\right)+\left[\ell(\ell+1) \sin ^{2} \theta-m^{2}\right] \Theta=0\)(3.16)

es más complicado. Con\(\cos \theta=z\) la solución es

\(P_{\ell}^{m}(z):=\left(1-z^{2}\right)^{|m| 2}\left(\frac{d}{d z}\right)^{|m|} P_{\ell}(z)\)(3.17)

donde\(P_{ℓ}(z)\) es el polinomio de Legendre\(ℓ\) -ésimo, definido por la siguiente fórmula, (llamada fórmula Rodrigues):

\(P_{\ell}(z):=\frac{1}{2^{\ell} \ell !}\left(\frac{d}{d z}\right)^{\ell}\left(z^{2}-1\right)^{\ell}\)(3.18)

Las funciones\(P_{\ell}^{m}(z)\) se denominan funciones asociadas de Legendre.

Problema 3.1

Encuentra los tres primeros polinomios de Legendre\(P_{0}(z)\),\(P_{1}(z)\) y\(P_{2}(z)\).

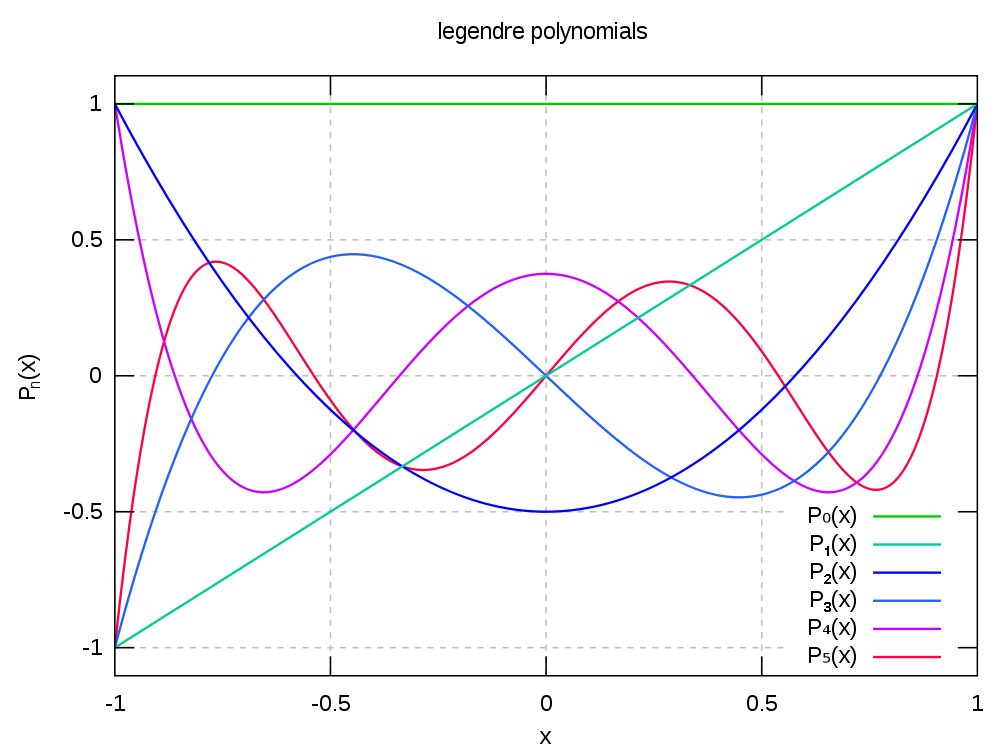
Figura 3.1: Trama de los primeros seis polinomios de Legendre.
http://en.Wikipedia.org/wiki/File:Legendrepolynomials6.svg

La función\(P_{\ell}^{m}(z)\) es un polinomio en z solo si\(|m|\) es par, de lo contrario contiene un término\(\left(1-z^{2}\right)^{|m| / 2}\) que es una raíz cuadrada. Pero al volver a\(cosθ=z\) este factor se reduce a\((\sin \theta)^{|m|}\).

Problema 3.2

Encontrar\(P_{2}^{0}(\theta)\),\(P_{2}^{1}(\theta)\),\(P_{2}^{2}(\theta)\).

Problema 3.3

Demostrar que\(P_{ℓ}(z)\) son soluciones de (3.16) para\(m=0\).

Problema 3.4

Demostrar que\(P_{\ell}^{m}(z)\) son soluciones de (3.16) para todos\(ℓ\) y\(|m|\), si\(|m|≤ℓ\).

Problema 3.5

Demostrar que\(P_{ℓ}(z)\) son pares, o impares dependiendo de la paridad de\(ℓ\).

Observe que\(ℓ\) debe ser un entero no negativo de lo contrario la definición (3.18) no tiene sentido, y además si | (|m|>l\), entonces (3.17) rinde cero. Así, para cualquier dado\(ℓ\), hay valores\(2ℓ+1\) permitidos de m:

\(m=-\ell,-\ell+1, \ldots-1,0,1, \ldots \ell-1, \ell, \quad \text { for } \quad \ell=0,1,2, \ldots\)(3.19)

Tenga en cuenta que la ecuación (3.16) —como todas las ecuaciones diferenciales de segundo orden— debe tener otras soluciones linealmente independientes diferentes de\(P_{\ell}^{m}(z)\) para un valor dado de\(ℓ\) y m. Sin embargo, se puede demostrar que estas últimas soluciones son divergentes para\(θ=0\) y\(θ=π\), por lo tanto, no están describiendo estados físicos. Las soluciones

\(Y_{\ell}^{m}(\theta, \phi)=\mathcal{N}_{l m} P_{\ell}^{m}(\theta) e^{i m \phi}\)(3.20)

donde los valores absolutos de las constantes\(\mathcal{N}_{l m}\) aseguran la normalización sobre la esfera unitaria, se denominan armónicos esféricos. Existen varias convenciones diferentes para las fases de\(\mathcal{N}_{l m}\), por lo que hay que tener cuidado con ellas.

Las\(Y_{\ell}^{m}(\theta)\) funciones son así las funciones propias de\(\hat{L}\) corresponder al valor propio\(\hbar^{2} \ell(\ell+1)\), y también son funciones propias de\(\hat{L}_{z}=-i \hbar \partial_{\phi}\), porque

\(\hat{L}_{z} Y_{\ell}^{m}(\theta, \phi)=-i \hbar \partial_{\phi} Y_{\ell}^{m}(\theta, \phi)=\hbar m Y_{\ell}^{m}(\theta, \phi)\)(3.21)

El número cuántico\(ℓ\) se denomina número cuántico de momento angular, o a veces por una razón histórica como número cuántico azimutal, mientras que m es el número cuántico magnético.

Concluyendo la subsección señalemos el siguiente dato importante. Como ninguno de los componentes de\(\mathbf{\hat{L}}\), y por lo tanto ni\(\hat{L}^{2}\) depende de la distancia radial rr desde el origen, entonces cualquier función de la forma\(\mathcal{R}(r) Y_{\ell}^{m}(\theta, \phi)\) será la solución de la ecuación de valor propio anterior, porque desde el punto de vista de la\(\mathbf{\hat{L}}\) la\(\mathcal{R}(r)\) función es una constante, y nosotros puede multiplicar libremente ambos lados de (3.8). por\(\mathcal{R}(r)\).

Ortonormalidad e integridad

Los armónicos esféricos forman un sistema infinito de funciones ortonormales en el sentido:

\(\int_{0}^{2 \pi} \int_{0}^{\pi}\left(Y_{\ell^{\prime}}^{m^{\prime}}(\theta, \phi)\right)^{*} Y_{\ell}^{m}(\theta, \phi) \sin \theta d \theta d \phi=\delta_{\ell \ell^{\prime}} \delta_{m m^{\prime}}\)(3.22)

Este sistema también es completo, lo que significa que cualquier función de valor complejo\(g(θ,ϕ)\) que sea integrable al cuadrado en la esfera unitaria, es decir, se\(\int|g(\theta, \phi)|^{2} \sin \theta d \theta d \phi<\infty\) puede ampliar en términos de\(Y_{\ell}^{m}(\theta, \phi)\)):

\(g(\theta, \phi)=\sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{\ell} c_{\ell m} Y_{\ell}^{m}(\theta, \phi)\)(3.23)

donde los coeficientes de expansión se pueden obtener de manera similar al caso de la expansión compleja de Fourier mediante

\(c_{\ell m}=\int_{0}^{2 \pi} \int_{0}^{\pi}\left(Y_{\ell}^{m}(\theta, \phi)\right)^{*} g(\theta, \phi) \sin \theta d \theta d \phi\)(3.24)

Lectura adicional

Si te interesa el tema Armónicos esféricos con más detalles echa un vistazo al enlace de Wikipedia a continuación:
http://en.Wikipedia.org/wiki/Spherical_harmonics

Animación

La animación muestra la dependencia del tiempo del estado estacionario, es decir, el que contiene\(e_{−iϵt/ℏ}\) también el factor dependiente del tiempo, dada por la función\(Y_{1}^{3}(θ,ϕ)\). El valor absoluto de la función en la dirección dada por\(θ\) y\(ϕ\) es igual a la distancia del punto desde el origen, y el argumento del número complejo se obtiene por los colores de la superficie de acuerdo con el código de fase del número complejo en la dirección elegida.

http://titan.physx.u-szeged.hu/~mmquantum/videok/Gombfuggveny_fazis_idofejlodes.flv

Animación

Las figuras muestran los diagramas polares tridimensionales de los armónicos esféricos. El estado a mostrar, se puede elegir estableciendo los números cuánticos\(ℓ\) y m.

http://titan.physx.u-szeged.hu/~mmquantum/interactive/Gombfuggvenyek.nbp

Ejemplos específicos

Las primeras funciones son las siguientes, con una de las convenciones habituales de fase (signo):

\(Y_{0}^{0}(\theta, \phi)=\frac{1}{\sqrt{4} \pi}\)(3.25)

\(Y_{1}^{0}(\theta, \phi)=\sqrt{\frac{3}{4 \pi}} \cos \theta, \quad Y_{1}^{1}(\theta, \phi)=-\sqrt{\frac{3}{8 \pi}} \sin \theta e^{i \phi}, \quad Y_{1}^{-1}(\theta, \phi)=\sqrt{\frac{3}{8 \pi}} \sin \theta e^{-i \phi}\)(3.26)

Históricamente los armónicos esféricos con las etiquetas se\(ℓ=0,1,2,3,4\) denominan\(s, p, d, f, g \ldots\) funciones respectivamente, la terminología proviene de la espectroscopia.

Si\(\mathbf{B}=\{0,0, B\}\) se aplica un campo magnético externo, la proyección del momento angular sobre la dirección del campo es\(ℏm\). Dado que mm puede tomar solo los valores enteros entre\(−ℓ\) y\(+ℓ\), hay\(2ℓ+1\) diferentes proyecciones posibles, correspondientes a las\(2ℓ+1\) diferentes funciones\(Y_{m}^{ℓ}(θ,ϕ)\) con un dado\(ℓ\).

Muy a menudo los armónicos esféricos están dados por coordenadas cartesianas explotando\(\sin \theta e^{\pm i \phi}=(x \pm i y) / r\) y\(\cos \theta=z / r\). Otra forma de usar estas funciones es crear combinaciones lineales de funciones con m -s opuestos. Esto es útil, por ejemplo, cuando ilustramos la orientación de los enlaces químicos en las moléculas. Esto lo demostramos con el ejemplo de las funciones p.

\ (\ begin {alineado}
&p_ {x} =\ frac {x} {r} =\ frac {\ left (Y_ {1} ^ {-1} -Y_ {1} ^ {1}\ derecha)} {\ sqrt {2}} =\ sqrt {\ frac {3} {4\ pi}}\ sin\ theta\ cos\ phi\
&p_ {x} =\ frac {y} {r} =-\ frac {\ izquierda (Y_ {1} ^ {-1} +Y_ {1} ^ {1}\ derecha)} {\ sqrt {2}} =\ sqrt {\ frac {3} {4\ pi}}\ sin\ theta\ sin\ phi\
&p _ {z} =\ frac {z} {r} =Y_ {1} ^ {0} =\ sqrt {\ frac {3} {4\ pi}}\ cos\ theta
\ end {alineado}\) (3.27)

Observemos también que las\(m=0\) funciones no dependen de ellas\(ϕ\), y son proporcionales a los polinomios de Legendre en\(cos⁡θ\).

\(Y_{\ell}^{0}(\theta)=\sqrt{\frac{2 \ell+1}{4 \pi}} P_{\ell}(\cos \theta)\)(3.28)

Paridad e impulso angular

El operador de paridad\(Π\) se define de la siguiente manera:

\(\Pi \psi(\mathbf{r})=\psi(-\mathbf{r})\)(3.29)

El resultado de actuar por la paridad sobre una función es la imagen especular de la función original con respecto al origen. Buscando los valores propios y las funciones propias de\(Π\), notamos primero que\(Π^{2}=1\). Por lo tanto, el valor propio único de\(Π^{2}\) es 1, y cualquier función es su función propia. Los valores propios de\(Π\) sí son entonces\(±1\), y tenemos las siguientes dos posibilidades:

\ (\ begin {alineado}
&\ pi_ {\ psi_ {+}} (\ mathbf {r}) =\ quad\ psi_ {+} (-\ mathbf {r}) =\ psi_ {+} (\ mathbf {r})\\
&\ pi_ {\ psi_ {-}} (\ mathbf {r}) = quad\ psi_ {-} (-\ mathbf {r}) =-\ psi_ {-} (\ mathbf {r})
\ final {alineado}\) (3.30)

En el primer caso las funciones propias\(\psi_{+}(\mathbf{r})\) que pertenecen al valor propio +1 son las funciones pares, mientras que en el segundo vemos que\(\psi_{-}(\mathbf{r})\) son las funciones impares que pertenecen al valor propio −1. Por supuesto, hay funciones que no son ni pares ni impares, no pertenecen al conjunto de funciones propias de\(Π\).

Figura 3.2: Ejemplos de funciones pares e impares en una y dos dimensiones.

La razón por la que consideramos la paridad en relación con el momento angular es que las funciones propias simultáneas\(\hat{L}^{2}\) y\(\hat{L}_{z}\) los armónicos esféricos multiplicados por cualquier función de la variable radial r\(Π\) también son funciones propias de, y los valores propios correspondientes son \((−1)^{ℓ}\). Esto puede formularse como:

\(\Pi \mathcal{R}(r) Y_{\ell}^{m}(\theta, \phi)=\mathcal{R}(r) \Pi Y_{\ell}^{m}(\theta, \phi)=(-1)^{\ell} \mathcal{R}(r) Y(\theta, \phi)\)(3.31)

Problema 3.6

Demostrar que la transformación\(\{x, y, z\} \longrightarrow\{-x,-y,-z\}\) es equivalente a\(\theta \longrightarrow \pi-\theta, \quad \phi \longrightarrow \phi+\pi\).

Figura 3.3: El efecto de la transformación\(\{x, y, z\} \longrightarrow\{-x,-y,-z\}\)

Problema 3.7

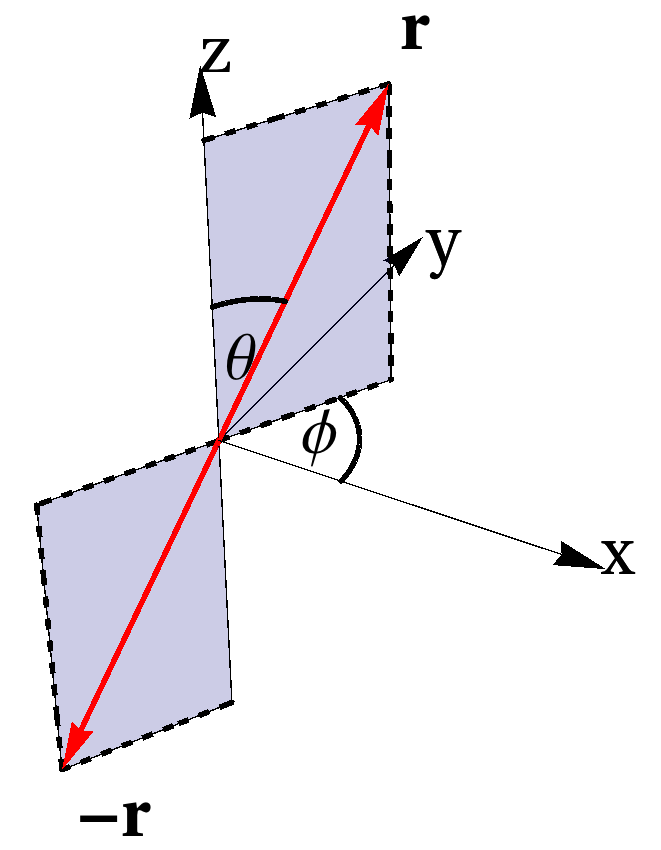
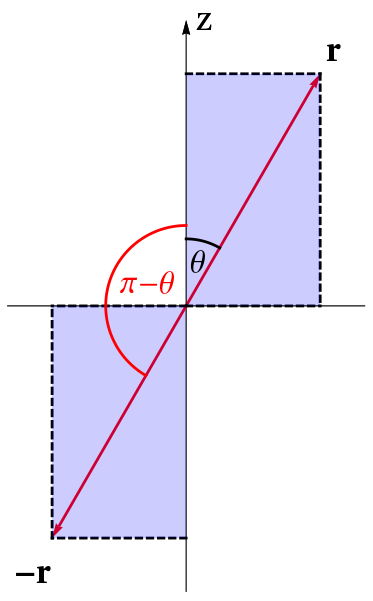
Mediante el uso de los resultados de las subsecciones anteriores se comprueba la validez de la Ec. (3.31).