4: Espectros atómicos, modelos simples de átomos

Objetivos

La mecánica cuántica tuvo inicialmente el objetivo de explicar los espectros lineales de los átomos vistos en la espectroscopia óptica. El primer intento exitoso fue el modelo de Bohr basado en postulados aparentemente “ad hoc”. Estos postulados son en realidad consecuencias del elegante tratamiento matemático del problema de Coulomb basado en los primeros principios de la mecánica cuántica. La aparición del momento angular en este caso especial insinúa su importancia en la física cuántica.

Requisitos previos

El problema de Kepler-Newton en la mecánica clásica, Capítulo 3.

Los postulados de Bohr y el modelo de Bohr

La mecánica cuántica tuvo inicialmente el objetivo de explicar los espectros lineales de los átomos vistos en la espectroscopia óptica. Posteriormente se convirtió en una teoría fundamental que explica todos los fenómenos microscópicos, incluyendo la física de partículas moleculares, de estado sólido, nuclear y de alta energía.

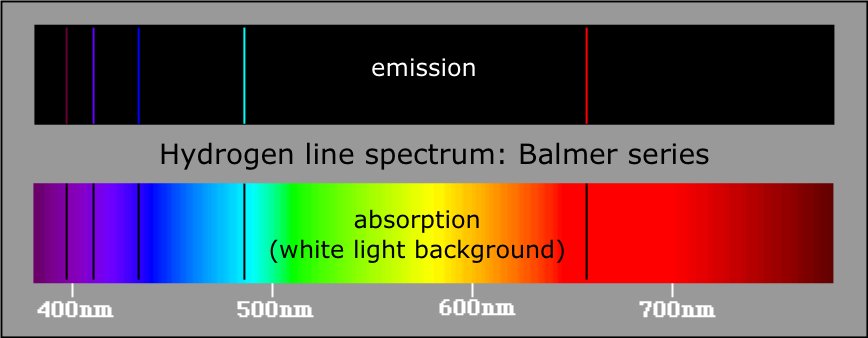
Figura 4.1: Espectros de emisión y absorción de la serie Balmer de hidrógeno.
http://www.goiit.com/posts/list/community-shelf-the-bohr-atom-917720.htm

Antes de entrar en algunos detalles de la explicación mecánica cuántica, primero recordamos cómo Niels Bohr explicó los espectros de los gases atómicos. Estableció dos postulados.

• Entre las órbitas clásicamente permitidas del electrón que se mueven alrededor del núcleo, existen ciertas órbitas estacionarias o estados estacionarios con energía definida. Los átomos no irradian si el electrón está en una órbita estacionaria de este tipo.
• Los electrones solo pueden ganar y perder energía saltando de una órbita permitida con energía\(E_{1}\) a otra, con\(E_{2}\) absorción o emisión de radiación electromagnética con una frecuencia\(\nu\) determinada por la diferencia de energía de los niveles según la relación de Planck:

\ (\ begin {alineado}
\ text {absorbtion}: & h\ nu=e_ {2} -E_ {1} &\ text {if}\ quad E_ {2} >E_ {1}\
\ text {emisión} &:\ quad h\ nu=e_ {1} -E_ {2} &\ text {si}\ quad E_ {1} >E_ {2}
\ end {alineado}\) (4.1)

donde h es la constante de Planck.

Estos postulados no pueden ser entendidos sobre la base de la física clásica. Un electrón que se mueve alrededor del núcleo tiene una aceleración centrípeta, y como todas las cargas eléctricas aceleradas se espera que irradie y pierda energía. Esto eventualmente dejaría caer en el núcleo, por lo que el átomo no podría ser un objeto estable, lo que está en aguda contradicción con las observaciones. Por lo tanto, los postulados parecían ser “ad hoc”. Aún así fueron muy significativas, porque estas afirmaciones resultaron ser ciertas a la vista de la “verdadera” mecánica cuántica, también. En esa teoría, sin embargo, estas no son afirmaciones fundamentales sino consecuencias de los principios generales más profundos y formalismo de la mecánica cuántica.

Además de estos postulados Bohr estableció una regla para el\(H\) átomo cómo las energías estacionarias discretas pueden ser obtenidas nuevamente por una condición cuántica ad hoc. Él prescribió que en estas órbitas estacionarias el momento angular\(ℓ\) del electrón que orbita sobre un círculo puede tener solo valores discretos, es decir, un múltiplo entero de\(ℏ=h/2π\) la constante de Planck dividido por\(2π\):

\(\mathcal{L}=m v r=n \hbar, \quad n=1,2 \ldots\)(4.2)

Esto se llama condición de cuantificación de Bohr. Combinando esto con la ecuación de movimiento del electrón:

\(\frac{q_{0}^{2}}{4 \pi \epsilon_{0}} \frac{1}{r^{2}}=m \frac{v^{2}}{r}\)(4.3)

es decir, la fuerza (Coulomb) es igual a los tiempos másicos (centrípeta) de aceleración, la energía total del electrón en la órbita circular, de radio r puede calcularse a partir de la expresión,

\(E=\frac{m v^{2}}{2}-\frac{q_{0}^{2}}{4 \pi \epsilon_{0}} \frac{1}{r}\)(4.4)

donde el primer término es la energía cinética mientras que el segundo es la energía potencial del electrón en el campo eléctrico del núcleo puntiforme, se pueden derivar dos resultados importantes. Introduciendo las notaciones

\(e_{0}^{2}=\frac{q_{0}^{2}}{4 \pi \epsilon_{0}} \quad a_{0}=\frac{\hbar^{2}}{m e_{0}^{2}}\)(4.5)

primero, los valores de energía permitidos de los estados estacionarios se obtienen como

\(E_{n}=-\frac{m e_{0}^{4}}{2 \hbar^{2}} \frac{1}{n^{2}}=-\frac{e_{0}^{2}}{2 a_{0}} \frac{1}{n^{2}} \quad n=1,2 \ldots\)(4.6)

Segundo, los valores permitidos de los radios de las órbitas estacionarias son:

\(r_{n}=a_{0} n^{2}\)(4.7)

\(a_{0}\)se llama el primer radio de Bohr y su valor es\(a_{0}=0.053nm\), y

\ (\ begin {alineado}
&E_ {n} =E_ {1}\ frac {1} {n^ {2}}\\
&E_ {1} =-2.2\ mathrm {aJ} =-13.6\ mathrm {eV} =-1\ text {Rydberg} =-1/2\ mathrm {hartree}
\ end {alineado}\) (4.8)

El signo negativo significa que el electrón está en un estado enlazado, ya que el nivel cero de la energía potencial está en\(r=∞\), donde el electrón se vuelve libre y tiene energía cero si\(\nu=0\). El estado con este menor valor de energía se denomina estado fundamental del átomo de H, y\(−E_{1}\) es la energía mínima que se le da a un átomo de H para ionizarlo, es decir, para desprender el electrón del núcleo. Estos resultados estuvieron de acuerdo con las observaciones experimentales del espectro de líneas de emisión de hidrógeno atómico, las diferentes series, etc. con la fórmula de Rydberg (Ver Figura 4.2).

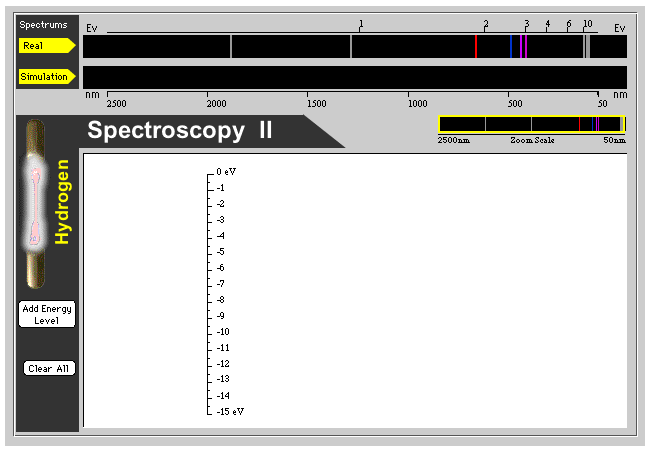
Figura 4.2: Visualización de las líneas del espectro de emisión de hidrógeno atómico.
http://hyperphysics.phy-astr.gsu.edu/hbase/hyde.html

Problema 4.1

Calcular las longitudes de onda de las primeras cuatro líneas de Balmer que corresponden a transiciones que llegan al nivel con\(n=2\). ¿Cuál es el límite de estas líneas donde comienza el continuum?

Sea, como es, gracioso, los resultados anteriores sí resultaron ser ciertos, aunque las premisas de las que partimos estaban definitivamente equivocadas. Existe una condición de cuantificación para el momento angular dado pero en un sentido muy diferente al dado en el modelo de Bohr. Y esta condición de cuantificación es más bien el resultado de los principios más profundos de la mecánica cuántica —explicados en la sección 2— que de una suposición apriori. Por lo que esta coincidencia accidental muestra que a partir de la premisa de inicio se puede llegar a cualquier resultado, incluyendo el ce correcto. Suposición similar no condujo sin embargo a resultados razonables en el caso de átomos más complicados, y tuvo que ser abandonada en la vista de la mecánica cuántica.

Animación

Podemos investigar el origen de las líneas espectrales en varios pasos con esta animación interactiva de ondas de choque.

http://phys.educ.ksu.edu/vqm/free/h2spec.html

La ecuación radial de la mecánica cuántica

La ecuación de valor propio de energía de Schrödinger para cualquier problema de campo central, incluyendo en particular el potencial de Coulomb tiene la forma

\(-\frac{\hbar^{2}}{2 m} \Delta \psi(\mathbf{r})+V(|\mathbf{r}|) \psi(\mathbf{r})=\varepsilon \psi(\mathbf{r})\)(4.9)

donde la energía potencial depende únicamente del valor,\(|\mathbf{r}|=r\) es decir, de la distancia desde un centro.

Ahora vamos a delinear el procedimiento de cómo se pueden obtener matemáticamente los valores propios de la energía y los estados estacionarios, restringiéndonos solo a los estados ligados, que juegan un papel muy importante en la física atómica, no sólo en el caso del átomo H. Para encontrar la solución de esta ecuación se introducen coordenadas esféricas,\(\psi(\mathbf{r})=\psi(r, \theta, \phi)\) indicadas por la simetría esférica del potencial. La ecuación del valor propio toma la forma

\(-\frac{\hbar^{2}}{2 m}\left(\Delta_{r}+\frac{1}{r^{2}} \Delta_{\theta \phi}\right) \psi(r, \theta, \varphi)+V(r) \psi(r, \theta, \varphi)=\varepsilon \psi(r, \theta, \phi)\)(4.10)

donde\(\) y\(Δ_{θϕ}\) son las partes radial y angular del Laplaciano, respectivamente. Separamos las partes radial y angular de la función de onda con el ansatz (suposición)

\(\psi(\mathbf{r})=\psi(r, \theta, \phi)=\mathcal{R}(r) Y_{\ell}^{m}(\theta, \phi)=\frac{u(r)}{r} Y_{\ell}^{m}(\theta, \phi)\)(4.11)

Usando los resultados de la sección anterior sobre el momento angular obtenemos la siguiente ecuación diferencial ordinaria para\(\mathcal{R}(r)\)

\(\frac{-\hbar^{2}}{2 m}\left(\frac{\partial^{2}}{\partial r^{2}}+\frac{2}{r} \frac{\partial}{\partial r}\right) \mathcal{R}(r)+\hbar^{2} \frac{1}{2 m} \frac{\ell(\ell+1)}{r^{2}} \mathcal{R}(r)+V(r) \mathcal{R}(r)=\varepsilon \mathcal{R}(r)\)(4.12)

Esto se llama la ecuación radial, cediendo

\(-\frac{\hbar^{2}}{2 m} \frac{d^{2} u}{d r^{2}}+\frac{\hbar^{2}}{2 m} \frac{\ell(\ell+1)}{r^{2}} u(r)+V(r) u(r)=\varepsilon u(r)\)(4.13)

para\(u(r)=r\mathcal{R}(r)\) lo cual también se llama a veces ecuación radial.

Problema 4.2

Mostrar que\(u(r)\) obedece a la ecuación (4.13).

Esta última forma para lo desconocido\(u(r)\) es similar a un problema unidimensional de valores propios, que contiene un potencial efectivo\(V(r)+\frac{\hbar^{2}}{2 m} \frac{\ell(\ell+1)}{r^{2}}\), donde el último término es un potencial centrífugo, apareciendo también en el problema clásico correspondiente en la forma\(\mathcal{L}^{2} / 2 m r^{2}\).

Comportamiento asintótico de las soluciones

Aintóticos en el infinito

Como suponemos que\(V(\infty) \rightarrow 0\), entonces para\(r \rightarrow \infty\) la energía potencial y la energía centrífuga son insignificantes y obtenemos la ecuación

\(-\frac{\hbar^{2}}{2 m} \frac{d^{2} u}{d r^{2}}=\varepsilon u\)(4.14)

Lo reescribimos como

\(\frac{d^{2} u}{d r^{2}}+\frac{2 m}{\hbar^{2}} \varepsilon u=0\)(4.15)

Si\(\), correspondiente\(ε≥0\), las dos soluciones son\(e^{ikr}\) y\(e^{−ikr}\). Como señalamos anteriormente estos no son integrables cuadrados. Los correspondientes\(\mathcal{R}(r)\) se comportan como

\(\mathcal{R}_{+}(r) \sim \frac{1}{r} e^{i(k r-\varepsilon t)} \quad \mathcal{R}_{-}(r) \sim \frac{1}{r} e^{-i(k r+\varepsilon t)} \quad \text { for } r \rightarrow \infty\)(4.16)

donde se incluyó la dependencia del tiempo para poder ver, que\(\mathcal{R}_{+}(r)\) describe una onda esférica saliente, un electrón con energía total positiva que puede dejar el átomo para\(r \rightarrow \infty\). \(\mathcal{R}_{-}(r)\)es una onda esférica entrante, y ambas se utilizan para la descripción de los procesos de dispersión, que aquí no analizamos.

Las soluciones integrables cuadradas se obtienen solo si\(ε<0\). Luego con la notación:

\(0<-\frac{2 m}{\hbar^{2}} \varepsilon=: \kappa^{2}\)(4.17)

las dos soluciones linealmente independientes apropiadas de la Ec. (4.15) son\(e^{κr}\) y\(e^{−κr}\), la primera de las cuales no es integrable al cuadrado en\([0, \infty)\) porque\(κ>0\). La segunda solución es adecuada, ya que decae exponencialmente para\(r \rightarrow \infty\), es por eso que conducirá al estado encuadernado, que es integrable al cuadrado. Así tenemos:

\(u(r \rightarrow \infty) \sim e^{-\kappa r}\)(4.18)

Aintóticos cerca del origen

Asumimos aquí que la energía potencial\(V(r)\) permanece finita en\(r=0\), o incluso si diverge eso no es más rápido que\(1/r^{2}\). El potencial Coulomb pertenece a esta clase, ya que es divergente sólo como\(1/r\). Luego en la ecuación radial (4.13) la energía potencial y se\(εu\) puede omitir además del término centrífugo dominante, llegando a la ecuación de segundo orden

\(\frac{d^{2} u}{d r^{2}}-\frac{\ell(\ell+1)}{r^{2}}=0\)(4.19)

que cuenta con dos soluciones\(r^{ℓ+1}\) y\(1/r^{ℓ}\).

Problema 4.3

Encuentra las soluciones de (4.19) en el formulario\(r^{k}\).

Mostrar que no\(1/r^{ℓ}\) es cuadrado integrable en\([0,∞)\), si\(ℓ>0\)

De acuerdo con la solución del problema anterior, la solución de la forma de no\(1/r^{ℓ}\) será apropiada si\(ℓ>0\), y por una argumentación un poco más sutil se puede demostrar que esto es válido para\(ℓ=0\), también. Esto significa que solo podemos permitirnos la solución no singular\(r^{ℓ+1}\) cercana a\(r=0\), es decir, la parte radial de la función de onda alrededor de 0 se comporta como.

\(\mathcal{R}(r)=u(r) / r \sim r^{\ell}\)(4.20)

es decir, va a cero si\(ℓeq0\), y permanece constante para\(ℓ=0\), es decir, para estados s.

La ecuación radial para los estados enlazados se puede escribir con la notación introducida en (4.17)

\(\frac{d^{2} u}{d r^{2}}-\frac{\ell(\ell+1)}{r^{2}} u-\frac{2 m}{\hbar^{2}} V(r) u=-\frac{2 m}{\hbar^{2}} \varepsilon u=\kappa^{2} u\)(4.21)

Será útil escribir la ecuación en términos de variable adimensional\(κr=ϱ\):

\(\left(\frac{d^{2}}{d \varrho^{2}}-\frac{\ell(\ell+1)}{\varrho^{2}}-\frac{V(\varrho / \kappa)}{|\varepsilon|}-1\right) u(\varrho)=0\)(4.22)

donde las condiciones asintóticas lo requieran\(u(\varrho \rightarrow 0) \sim \varrho^{\ell+1}\) y\(u(\varrho \rightarrow \infty) \sim e^{-\varrho}\).

Esta ecuación radial se utiliza a menudo en la física atómica, una solución en una forma analítica cerrada solo se puede obtener si el potencial\(V(r)\) tiene ciertas formas especiales. Por lo tanto, se suelen aplicar métodos numéricos para las soluciones. Para uno de los casos más importantes: el potencial tipo\(1/r\) Coulomb las soluciones pueden expresarse en términos de funciones analíticas elementales. En la siguiente sección se aborda este problema.

Problema de valor propio del potencial de Coulomb

En el caso del atractivo campo de Coulomb se escribirá la ecuación radial para el caso más general de iones similares a hidrógeno, donde está el número de protones en el núcleo\(Z≥1\), que unían un solo electrón. Ejemplos son el helio ionizado de manera individual:\(\mathrm{He}^{+}(Z=2)\), Litio doblemente ionizado\(\mathrm{Li}^{++}(Z=3)\), etc. La energía potencial es entonces\(V(r)=-\frac{Z e_{0}^{2}}{r}\), donde se usa la notación de la Ec. (4.5). Con\(κr=ϱ\),\(V(\varrho / \kappa)=-\frac{Z e_{0}^{2} \kappa}{\varrho}\), y el tercer término en la ecuación radial es\(\frac{V(\varrho / \kappa)}{|\varepsilon|}=-\frac{2 m Z e_{0}^{2}}{\hbar^{2} \kappa} \frac{1}{\varrho}=-\frac{\varrho_{0}}{\varrho}\). donde hemos introducido la notación:

\(\varrho_{0}=\frac{2 m Z e_{0}^{2}}{\hbar^{2} \kappa}=\frac{2 Z}{\kappa a_{0}}\)(4.1)

La ecuación radial en sí toma la forma:

\(\left(\frac{d^{2}}{d \varrho^{2}}-\frac{\ell(\ell+1)}{\varrho^{2}}+\frac{\varrho_{0}}{\varrho}-1\right) u(\varrho)=0\)(4.2)

De acuerdo a las condiciones asintóticas obtenidas en el subapartado anterior buscamos la solución como

\(u(\varrho)=\varrho^{\ell+1} w(\varrho) e^{-\varrho}\)(4.3)

donde el factor\(ϱ^{ℓ+1}\) cuida el comportamiento adecuado cercano a cero, el factor\(e^{−ϱ}\) al infinito, y\(w(ϱ)\) —que se va a determinar— debe asegurar que esta forma de\(u(ϱ)\) es la solución exacta de la ecuación (4.2). Poniendo la expresión de uu dada por (4.3) en (4.2), obtenemos la ecuación diferencial:

\(\varrho \frac{d^{2} w}{d \varrho^{2}}+2(\ell+1-\varrho) \frac{d w}{d \varrho}+\left(\varrho_{0}-2(\ell+1)\right) w=0\)(4.4)

La solución de la ecuación para no\(w(ϱ)\) debe viciar las formas asintóticas prescritas estipuladas por (4.3), lo que significa que\(w(ϱ)\) debe tener una serie de potencias (con exponentes positivos) alrededor de cero, y para\(ϱ→∞\) ello debe crecer más lento que\(e^{ϱ}\) para mantener la condición\(u(\varrho \rightarrow \infty) \sim e^{-\varrho}\) Si uno busca una solución

\(w(\varrho)=\sum_{k=0}^{\infty} a_{k} \varrho^{k}\)(4.5)

y lo sustituye en (4.4), se obtiene una relación de recurrencia entre los coeficientes:

\(a_{k+1}=\frac{2(k+\ell+1)-\varrho_{0}}{(k+1)(k+2 \ell+2)} a_{k}\)(4.6)

Además se puede demostrar que si las series (4.5) fueran infinitas, la relación de recurrencia se comportaría como la de la serie de potencia de la\(e^{2ϱ}\) cual significaría que la condición asintótica\(u(\varrho \rightarrow \infty) \sim e^{-\varrho}\) sería reemplazada por la\(u(\varrho \rightarrow \infty) \sim e^{\varrho}\) cual no estaba permitida, ya que requeríamos integrabilidad cuadrada. Por lo tanto, la suma en (4.5) debe permanecer finita. Esto significa que existe un entero\(n_{r}\), para el cual\(a_{n_{r}} e q 0\), pero\(a_{n_{r}+1}=0\), y luego, como se deduce de (4.6), all\(a_{k}=0\), for\(k>n_{r}\). En otras palabras, la suma\(w(ϱ)\) que da debe reducir a un polinomio de grado\(n_{r}\). Esto es posible, si y solo si el nominador del coeficiente de\(a_{n_{r}}\) dado por el lado derecho de (4.6) desaparece, así:

\(\varrho_{0}=2\left(n_{r}+\ell+1\right)\)(4.7)

El grado\(n_{r}\) del polinomio w se denomina como número cuántico radial. Ahora se introduce el número cuántico principal con la definición

\(n:=n_{r}+\ell+1\)(4.8)

que es un entero positivo. Se le da el nombre principal, porque este es el número cuántico que determina los valores propios de la energía. (Esta declaración se refinará más adelante). Para ver esto recordamos la notación introducida en (4.1)

\(\varrho_{0}=\frac{2 m Z e_{0}^{2}}{\hbar^{2} \kappa}=\frac{2 Z}{\kappa a_{0}}=2 n\)(4.9)

y conseguimos\(\kappa_{n}=\frac{Z}{n a_{0}}=\frac{2 m Z e_{0}^{2}}{\hbar^{2} n}\). De la definición de κ, es decir\(\varepsilon=-\frac{\hbar^{2} \kappa^{2}}{2 m}\), los valores propios correspondientes al potencial de Coulomb son los siguientes:

\(\varepsilon_{n}=-\frac{m Z^{2} e_{0}^{4}}{2 \hbar^{2}} \frac{1}{n^{2}}=-Z \frac{e_{0}^{2}}{2 a_{0}} \frac{1}{n^{2}}, \quad n=1,2 \ldots\)(4.10)

Este es el resultado más importante: resulta que la ecuación de valor propio de energía tiene soluciones integrables cuadradas solo si\(ε<0\), y además solo si ε es igual a ciertos números discretos, que son iguales a los obtenidos por Bohr a partir de su condición de cuantificación (errónea).

Los valores propios de energía de este espectro discreto se denominan las energías de estado unido del potencial de Coulomb.

Los valores propios concuerdan muy bien con los valores experimentales del espectro primario del átomo H de\((Z=1)\) la serie Lyman, Balmer etc. El resultado también concuerda con la fórmula obtenida del modelo Bohr. Pero el modelo Bohr funciona solo para el átomo H, es decir, para el potencial Coulomb, mientras que el procedimiento mecánico cuántico funciona bien con cualquier potencial.

Con el procedimiento anterior, se obtuvo el espectro discreto, donde se debe recordar el papel de las condiciones límite. Es importante, sin embargo, que también haya soluciones con\(ε>0\), donde ε puede ser cualquier número no negativo. La última parte de los valores propios forman el espectro continuo, y los estados propios correspondientes son los estados de dispersión. Estas funciones no son integrables cuadradas, pero de manera similar a las ondas De Broglie, se pueden formar a partir de ellas superposiciones continuas que a su vez son integrables cuadradas.

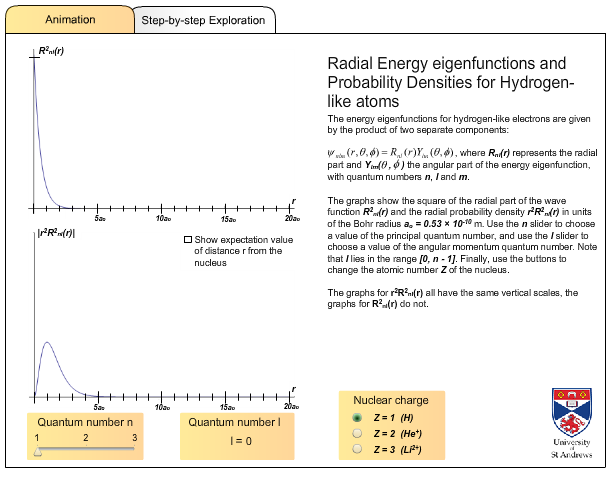
Figura 4.3: A la izquierda se puede ver el diagrama de energía de los estados estacionarios del átomo de hidrógeno. Mientras que a la derecha las cifras muestran las densidades de probabilidad de posición de las densidades electrón-núcleo en los estados\(\left(r^{2}\left|\mathcal{R}_{n \ell}(r)\right|^{2}\right)\).
http://www.kutl.kyushu-u.ac.jp/seminar/MicroWorld2_E/2Part3_E/2P32_E/hydrogen_atom_E.htm

Animación

Con esta animación flash puedes investigar las funciones propias radiales y las densidades de probabilidad\(\left(r^{2}\left|\mathcal{R}_{n \ell}(r)\right|^{2}\right)\) para átomos similares al hidrógeno.

http://www.st-andrews.ac.uk/~qmanim/embed_item_3.php?anim_id=50

Lectura adicional

Las formas explícitas de las funciones propias se pueden encontrar en varios libros, o en la url: http://panda.unm.edu/courses/finley/P262/Hydrogen/WaveFcns.html.

Lectura adicional

Aquí encontrarás una presentación sobre las diferentes posibilidades de visualizar el átomo de hidrógeno.
http://www.hydrogenlab.de/elektronium/HTML/einleitung_hauptseite_uk.html

Lectura adicional

isit the Grand Orbital Table: http://www.orbitals.com/orb/orbtable.htm, donde se\(n=10\) presentan todos los orbitales atómicos till.