1.4: El principio de incertidumbre

Las olas son borrosas

Como hemos demostrado para los paquetes de ondas, la naturaleza de onda de las partículas implica que no podemos conocer tanto la posición como el impulso de una partícula con un grado arbitrario de precisión, si\(\Delta x\) representa la incertidumbre en nuestro conocimiento de la posición, y\(\Delta p\) el del impulso, entonces

\[ \Delta p \Delta x \sim h \tag{1.4.1} \]

donde\(h\) está la constante de Planck. En el mundo real, las partículas son tridimensionales y deberíamos decir\[ \Delta p_x \Delta x \sim h \tag{1.4.2} \]

con ecuaciones correspondientes para las otras dos direcciones espaciales. La confusión sobre la posición está relacionada con la del impulso en la misma dirección.

Veamos cómo funciona esto tratando de medir la posición y y y el impulso con mucha precisión. Supongamos que tenemos una fuente de electrones, digamos, un cañón de electrones en un CRT (tubo de rayos catódicos, como un monitor anticuado). El haz se extiende un poco, pero si interponemos una lámina de metal con una hendidura de ancho\(w\), entonces para partículas que la hacen pasar por la hendidura, sabemos\(y\) con una incertidumbre\(\Delta y=w\). Ahora bien, si la rendija está muy lejos aguas abajo de la fuente del cañón de electrones, también sabemos con\(p_y\) mucha precisión a medida que el electrón llega a la rendija, porque para llegar a la hendidura la velocidad del electrón tendría que ser apuntada justo.

Pero, ¿afecta la medida de la posición y del electrón —en otras palabras, el hecho de que pase por la rendija— su impulso y? La respuesta es sí. Si no lo hacía, entonces al enviar una corriente de partículas a través de la hendidura, todas golpearían muy cerca del mismo punto en una pantalla colocada más aguas abajo. Pero sabemos por experimento que esto no es lo que sucede: se acumula un patrón de difracción de hendidura única, de ancho angular\(\theta \sim \lambda/w\), donde la longitud de onda\(\lambda\) de Broglie del electrón viene dada por\(p_x \cong h/\lambda\) (hay una contribución insignificante a\(\lambda\) partir del impulso y). La consiguiente incertidumbre en\(p_y\) es

\[ \Delta p_y/p_x \sim \theta \sim \lambda/w \tag{1.4.3} \]

Poniendo\(p_x = h/\lambda\), enseguida encontramos que

\[ \Delta p_y \sim h/w \tag{1.4.4} \]

por lo que el acto de medir la posición y del electrón ha esfumado su impulso y precisamente en la cantidad requerida por el principio de incertidumbre.

Tratando de vencer el principio de incertidumbre

Para entender mejor el Principio de Incertidumbre, tratemos de ver qué sale mal cuando en realidad tratamos de medir la posición y el impulso con mayor precisión de lo permitido.

Por ejemplo, supongamos que miramos un electrón a través de un microscopio. ¿Qué podríamos esperar ver? Por supuesto, ya sabes que si tratamos de mirar algo realmente pequeño a través de un microscopio se vuelve borroso: un pequeño objeto afilado obtiene patrones de difracción alrededor de sus bordes, lo que indica que estamos viendo algo de tamaño comparable a la longitud de onda de la luz que se está utilizando. Si miramos algo mucho más pequeño que la longitud de onda de la luz, como el electrón, esperaríamos un patrón de difracción de anillos concéntricos con una mancha circular en el medio. El tamaño del patrón es de orden la longitud de onda de la luz, de hecho a partir de la óptica se puede mostrar como\(\sim\lambda f/d\) donde\(d\) está el diámetro de la lente objeto del microscopio,\(f\) la distancia focal (la distancia de la lente al objeto). Tomaremos\(f /d \sim 1\), como suele ser. Entonces, mirar un objeto del tamaño de un electrón debería dar un patrón de difracción centrado en la ubicación del objeto. Eso parecería precisar su posición con bastante precisión.

¿Qué pasa con el impulso del electrón? Aquí surge un problema que no importa para objetos más grandes: la luz que vemos, por supuesto, ha rebotado en el electrón, y así el electrón tiene cierto impulso de retroceso. Es decir, al hacer rebotar luz del electrón le hemos dado cierto impulso. ¿Podemos decir cuánto? Para hacerlo sencillo, supongamos que tenemos buenos ojos y solo necesitamos hacer rebotar un fotón del electrón para verlo. Conocemos el momento inicial del fotón (porque conocemos la dirección del haz de luz que estamos usando para iluminar el electrón) y sabemos que después de rebotar, el fotón golpea la lente del objeto y pasa por el microscopio, pero no sabemos dónde el fotón choca con la lente objeto. El objetivo de un microscopio es que toda la luz de un punto, luz que incide en la lente del objeto en diferentes lugares, esté enfocada de nuevo a un punto, formando la imagen (aparte de la borrosidad mencionada anteriormente). Entonces, si la luz tiene longitud de onda\(\lambda\), sus fotones constituyentes tienen impulso\(\sim h/\lambda\), y de nuestra ignorancia de dónde entró el fotón al microscopio no estamos seguros de su impulso en dirección x en una cantidad\(\sim h/\lambda\). Necesariamente, entonces, tenemos la misma incertidumbre sobre el impulso de la dirección x del electrón, ya que esto fue impartido por el fotón que rebotaba.

Pero ahora tenemos un problema. En nuestros intentos de minimizar la incertidumbre en el momento del electrón, usando solo un fotón para detectarlo, no vamos a ver gran parte del patrón de difracción discutido anteriormente, tales patrones de difracción son generados por muchos fotones que golpean la película, retina o cualquier equipo de detección que sea siendo utilizado. Un solo fotón genera un solo punto (¡en el mejor de los casos!). Lo más probable es que este punto esté dentro\(\lambda\) del orden del centro del patrón, pero esto nos deja con una incertidumbre en la posición de orden \(\lambda\).

Por lo tanto, al intentar observar la posición y el impulso de un solo electrón utilizando un solo fotón, encontramos una incertidumbre en la posición\(\Delta x\sim\lambda\) y en el impulso\(\Delta p_x\sim h/\lambda\). Estos resultados están de acuerdo con el Principio de Incertidumbre de Heisenberg\(\Delta x\Delta p_x\sim h\).

Por supuesto, podríamos precisar la posición mucho mejor si usáramos\(N\) fotones en lugar de uno solo. A partir de la teoría estadística, se sabe que la incertidumbre restante\(\sim \lambda/\sqrt{N}\). Pero entonces los\(N\) fotones han rebotado en el electrón, por lo que, dado que es igualmente probable que cada uno haya pasado por cualquier parte de la lente del objeto, la incertidumbre en el impulso del electrón como consecuencia de estas colisiones sube como\(\sqrt{N}\). (Lo mismo que el desequilibrio promedio entre cabezas y colas en una secuencia de\(N\) volteos de monedas).

Al señalar que la incertidumbre en el impulso del electrón surge porque no sabemos dónde pasa el fotón rebotado a través de la lente del objeto, es tentador pensar que solo podríamos usar una lente de objeto más pequeña, eso reduciría\(\Delta p_x\). Si bien esto es correcto, recordemos desde arriba que afirmamos que el tamaño del patrón de difracción era\(\sim \lambda f/d\), donde\(d\) está el diámetro de la lente objeto y\(f\) su distancia focal. Es fácil ver que el patrón de difracción, y consecuentemente\(\Delta x\), se hace más grande por solo la cantidad que\(\Delta p_x\) se hace más pequeña!

Observando electrones en el experimento de doble rendija

Supongamos ahora que en el experimento de doble rendija, nos propusimos detectar por qué hendidura pasa cada electrón brillando una luz justo detrás de la pantalla y observando la luz reflejada del electrón inmediatamente después de haber pasado por una rendija. Después de la discusión en las Conferencias de Física de Feynman, Volumen III, estableceremos ahora que si podemos detectar los electrones, ¡arruinamos el patrón de difracción!

Tomando la distancia entre las dos ranuras para ser\(d\), las líneas oscuras en el patrón de difracción están en ángulos\[ (n+\frac{1}{2})\lambda_{elec}=d\sin\theta \tag{1.4.5} \]

Si la luz utilizada para ver qué hendidura atraviesa el electrón genera una incertidumbre en el momento y del electrón\(\Delta p_y\) 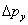, para no destruir el patrón de difracción debemos tener\[ \Delta p_y/p <\lambda_{elec}/d \tag{1.4.6} \]

(la incertidumbre angular en la dirección del electrón no debe ser suficiente para propagarlo desde los máximos del patrón de difracción a los mínimos). Aquí\(p\) está el impulso completo del electrón,\(p=h/\lambda_{elec}\). Ahora bien, la incertidumbre en el impulso y del electrón, buscándolo con un microscopio, lo es\(\Delta p_y \sim h/\lambda_{light}\).

Sustituyendo estos valores en la desigualdad anterior encontramos que la condición para que el patrón de difracción sobreviva es\[ \lambda_{light}>d \tag{1.4.7} \]

la longitud de onda de la luz utilizada para detectar qué hendidura atravesó el electrón debe ser mayor que la distancia entre las hendiduras. Desafortunadamente, la luz dispersada del electrón le da entonces a un punto en un patrón de difracción de tamaño la longitud de onda de la luz utilizada, así que incluso si vemos el destello esto no precisa al electrón lo suficiente como para decir por qué hendidura atravesó. Heisenberg vuelve a ganar.

Cómo determina el principio de incertidumbre el tamaño de todo

Es interesante ver cómo el tamaño físico real del átomo de hidrógeno está determinado por la naturaleza de onda del electrón, en efecto, por el Principio de Incertidumbre. En el estado fundamental del átomo de hidrógeno, el electrón minimiza su energía total. Para un átomo clásico, la energía sería menos infinito, asumiendo que el núcleo es un punto (y muy grande en todo caso) porque el electrón se sentaría justo encima del núcleo. Sin embargo, esto no puede suceder en la mecánica cuántica. Un electrón tan localizado tendría una incertidumbre muy grande en el momento, es decir, la energía cinética sería grande. Esto se ve más claramente imaginando que el electrón va en una órbita circular de radio \(r\)con momento angular\(h/2p\). Entonces una longitud de onda de la onda de Broglie del electrón simplemente cabe alrededor del círculo,\(\lambda_{elec}=2\pi r\). Claramente, a medida que reducimos el radio del círculo\(r\),\(\lambda_{elec}\) baja proporcionalmente, y el impulso de los electrones

\[ p=h/\lambda_{elec}=h/2\pi r \tag{1.4.8} \]

aumenta. Añadiendo la energía potencial electrostática del electrón encontramos que la energía total para una órbita circular de radio\(r\) es:

\[ E(r)=K.E.+P.E.=\frac{p^2}{2m}-\frac{e^2}{4\pi \varepsilon_0r}=\frac{h^2}{8m\pi^2r^2}-\frac{e^2}{4\pi\varepsilon_0r} \tag{1.4.9} \]

Observe que para muy grandes\(r\), la energía potencial domina, la energía cinética es insignificante, y la contracción del átomo disminuye la energía total. Sin embargo, por lo suficientemente pequeño\(r\), el término de energía cinética (siempre positivo) gana, y la energía total crece a medida que el átomo se contrae. Evidentemente, entonces, debe haber un valor\(r\) para el cual la energía total sea mínima. Visualizar una gráfica de la energía total dada por la ecuación anterior en función de\(r\), en el punto mínimo la pendiente de\(E(r)\) es cero,\(dE(r)/dr=0\).

Es decir,

\[ -\frac{h^2}{4m\pi^2r}+\frac{e^2}{4\pi \varepsilon_0}=0 \tag{1.4.10} \]

dando

\[ r_{min}=\frac{\varepsilon_0h^2}{\pi me^2} \tag{1.4.11} \]

La energía total para este radio es la respuesta exacta correcta, lo cual es tranquilizador (pero no lo merecemos, porque hemos usado una imagen ingenua, como quedará claro más adelante).

El objetivo de este ejercicio es ver que en la mecánica cuántica, a diferencia de la mecánica clásica, una partícula no puede posicionarse en el mínimo exacto de energía potencial, porque eso requeriría un paquete de ondas muy estrecho y por lo tanto sería caro en energía cinética. El estado fundamental de una partícula cuántica en un potencial atractivo es un equilibrio entre la minimización de energía potencial y la minimización de energía cinética. Así, los tamaños físicos de los átomos, las moléculas y, en última instancia, nosotros mismos están determinados por la constante de Planck.

Colaborador

• Michael Fowler (Beams Professor, Department of Physics, University of Virginia)