2.1: Serie de Fourier e Integrales, la Función Dirac

Comenzamos con una breve revisión de las series de Fourier. Cualquier función periódica de interés en la física puede expresarse como una serie en senos y cosenos; ya hemos visto que la función de onda cuántica de una partícula en una caja es precisamente de esta forma. La pregunta importante en la práctica es, para una función de onda arbitraria, qué tan buena se da una aproximación si dejamos de sumar la serie después de\(N\) términos. Establecemos aquí que la suma después de\(N\) términos\(f_N(\theta)\),, puede escribirse como una convolución de la función original con la función

\[ \delta_N(x)=(1/2\pi)(\sin(N+\dfrac{1}{2})x)/\sin\dfrac{1}{2}x \label{2.1.1} \]

es decir,

\[ f_N(\theta)=\int\limits_{-x}^{x} \delta_N(\theta-\theta')f(\theta')d\theta' \label{2.1.2} \]

La estructura de la función\(\delta_N(x)\) (trazada a continuación), cuando se junta con la función\(f(\theta)\), da una buena guía intuitiva de qué tan buena aproximación va a ser la suma sobre\(N\) términos para una función dada\(f(\theta)\). En particular, resulta que las discontinuidades escalonadas nunca se manejan a la perfección, sin importar cuántos términos se incluyan. Afortunadamente, las verdaderas discontinuidades escalonadas nunca ocurren en la física, pero esto es una advertencia de que por supuesto es necesario resumir algunos\(N\) donde los senos y cosenos oscilan sustancialmente más rápidamente que cualquier cambio repentino en la función que se representa.

Pasamos a la transformada de Fourier, en la que una función en la línea infinita se expresa como una integral sobre un continuo de senos y cosenos (o equivalentemente exponenciales\(e^{ikx}\)). Resulta que argumentos análogos a los que llevaron\(\delta_N(x)\) ahora a dar una función\(\delta(x)\) tal que

\[ f(x)=\int\limits_{-\infty}^{\infty} \delta(x-x')f(x')dx' \label{2.1.3} \]

Ante esto, uno bien podría preguntarse cuál es el sentido de una función\(\delta(x)\) que sobre la convolución con\(f(x)\) devuelve la misma función\(f(x)\). La relevancia de se\(\delta(x)\) hará evidente más adelante en el curso, cuando los estados de una partícula cuántica estén representados por funciones de onda en la línea infinita, como\(f(x)\), y las operaciones sobre ellas involucran operadores integrales similares a la convolución anterior. Trabajar con operaciones en estas funciones es la generalización continua de matrices que actúan sobre vectores en un espacio finito-dimensional, y\(\delta(x)\) es la representación infinito-dimensional de la matriz unitaria. Así como en el álgebra matricial los estados propios de la matriz unitaria son un conjunto de vectores que abarcan el espacio, y los elementos de la matriz unitaria determinan el conjunto de productos de puntos de estos vectores base, la función delta determina el producto interno generalizado de una base continua de estados. Desempeña un papel esencial en el formalismo estándar para los estados continuos, ¡y hay que estar familiarizado con él!

Serie de Fourier

Cualquier función real razonablemente suave\(f(\theta)\) definida en el intervalo\(-\pi<\theta\le\pi\) puede expandirse en una serie de Fourier,

\[ f(\theta)=\dfrac{A_0}{2}+\sum_{n=1}^{\infty} (A_n\cos n\theta +B_n\sin n\theta) \label{2.1.4} \]

donde los coeficientes se pueden encontrar usando la condición de ortogonalidad,

\[ \int\limits_{-\pi}^{\pi} \cos m\theta \cos n\theta d\theta=\pi\delta_{m,n} \label{2.1.5} \]

y la misma condición para que los\(\sin n\theta\)'s den:

\[ A_n=\dfrac{1}{\pi}\int\limits_{-\pi}^{\pi} f(\theta)\cos n\theta d\theta \label{2.1.6} \]

\[ B_n=\dfrac{1}{\pi}\int\limits_{-\pi}^{\pi} f(\theta)\sin n\theta d\theta \label{2.1.7} \]

Tenga en cuenta que para una función par, solo los\(A_n\) son distintos de cero, para una función impar solo los\(B_n\) son distintos de cero.

¿Qué tan suave es “razonablemente suave”?

El número de términos de la serie necesarios para dar una buena aproximación a una función depende de la rapidez con la que cambie la función. Para tener una idea de lo que sale mal cuando una función no es “suave”, es instructivo encontrar la serie sinusoidal de Fourier para la función step\[f(\theta)=-1 \;\; for \;\; -\pi<\theta\le0, \;\; f(\theta)=1 \;\; for \;\; 0<\theta\le\pi \label{2.1.8}\]

Usando la expresión para\(B_n\) arriba es fácil de encontrar:

\[ f(\theta)=\dfrac{4}{\pi} \left( \sin\theta +\dfrac{\sin 3\theta}{3}+\dfrac{\sin 5\theta}{5}+... \right) \label{2.1.9} \]

Tomando la primera media docena de términos de la serie da:

Fenómeno Gibbs'

A medida que incluimos más y más términos, la función se vuelve más suave pero, sorprendentemente, el sobreimpulso inicial en el escalón permanece en una fracción finita de la altura del escalón. No obstante, la función se recupera cada vez más rápidamente, es decir, el sobreimpulso y el “zumbido” en el escalón ocupan cada vez menos espacio. Este sobreimpulso se llama fenómeno de Gibbs, y solo ocurre en funciones con discontinuidades.

Cómo se relaciona la suma sobre N términos con la función completa

Para tener una idea más clara de cómo una serie de Fourier converge a la función que representa, es útil detener la serie en N términos y examinar cómo tiende esa suma, a la que\(f_N(\theta)\) denotamos\(f(\theta)\).

Entonces, sustituyendo los valores de los coeficientes (Ecuación\ ref {2.1.6} y\ ref {2.1.7})

\[ A_n=\dfrac{1}{\pi}\int\limits_{-\pi}^{\pi} f(\theta)\cos n\theta d\theta \nonumber \]

\[ B_n=\dfrac{1}{\pi}\int\limits_{-\pi}^{\pi} f(\theta)\sin n\theta d\theta \nonumber\]

en la serie (Ecuación\ ref {2.1.4})

\[ f_N(\theta)=\dfrac{A_0}{2}+\sum_{n=1}^{N} (A_n\cos n\theta +B_n\sin n\theta) \nonumber \]

da

\[ f_N(\theta)=\dfrac{1}{2\pi} \int\limits_{-\pi}^{\pi} f(\theta') d\theta' +\dfrac{1}{\pi}\sum_{n=1}^{N} \int\limits_{-\pi}^{\pi}(\cos n\theta\cos n\theta' +\sin n\theta\sin n\theta')f(\theta')d\theta'\]

\[=\dfrac{1}{2\pi} \int\limits_{-\pi}^{\pi} f(\theta') d\theta' +\dfrac{1}{\pi}\sum_{n=1}^{N} \int\limits_{-\pi}^{\pi}\cos n(\theta-\theta')f(\theta')d\theta' \label{2.1.10} \]

Ahora podemos usar la identidad trigonométrica

\[ \sum_{n=1}^{N} \cos nx= \dfrac{\sin (N+\dfrac{1}{2})x}{2\sin\dfrac{1}{2}x} -\dfrac{1}{2} \label{2.1.11}\]

para encontrar

\[ f_N(\theta)=\dfrac{1}{2\pi}\int\limits_{-\pi}^{\pi} \dfrac{\sin (N+\dfrac{1}{2})(\theta-\theta')}{\sin\dfrac{1}{2}(\theta-\theta')} f(\theta') d\theta'= \int\limits_{-\pi}^{\pi} \delta_N(\theta-\theta') f(\theta')d\theta' \label{2.1.12}\]

donde

\[ \delta_N(x)= \dfrac{1}{2\pi} \dfrac{\sin (N+\dfrac{1}{2})x}{\sin\dfrac{1}{2}x} \label{2.1.13}\]

(Tenga en cuenta que probar la identidad trigonométrica es sencillo: escribir\(z=e^{ix}\), así\(\cos nx=\dfrac{1}{2}(z^n+z^{-n})\), y sumar las progresiones geométricas.)

Ir hacia atrás por un momento y escribir

\[ \delta_N(x)= \dfrac{1}{\pi} \left(\sum_{n=1}^{N} \cos nx +\dfrac{1}{2} \right) \label{2.1.14}\]

es fácil comprobar que\[ \int\limits_{-\pi}^{\pi} \delta_N(x)dx=1 \label{2.1.15}\]

Para ayudar a visualizar\(\delta_N(\theta)\), aquí está\(N = 20\):

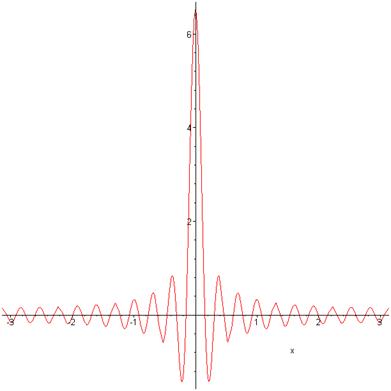
Acabamos de establecer que el área total bajo la curva = 1, y se desprende del diagrama que casi toda esta área está por debajo del pico central, ya que las áreas alejadas del centro son casi igualmente positivas y negativas. El ancho del pico central es\(\pi/(N+\dfrac{1}{2})\), su altura\((N+\dfrac{1}{2})/\pi\).

Ejercicio: para grandes\(N\), aproximadamente ¿qué tan abajo se hunde en la primera oscilación? (\(N/\pi^2\))

Para funciones que varían lentamente en comparación con las oscilaciones, la integral de convolución

\[ f_N(\theta)= \int\limits_{-\pi}^{\pi} \delta_N(\theta-\theta')f(\theta')d\theta' \label{2.1.16}\]

dará\(f_N(\theta)\) cerca de\(f(\theta)\), y para estas funciones\(f_N(\theta)\) tenderá a\(f(\theta)\) medida que N aumente.

También está claro por qué convolucionar esta curva con una función de paso da un sobreimpulso y oscilaciones. Supongamos que la función\(f(\theta)\) es un paso, saltando de 0 a 1 en\(\theta=0\) De la forma convolutiva de la integral, deberías poder convencerte de que el valor de\(f_N(\theta)\) en un punto\(\theta\) es el área total bajo la curva\(\delta_N(\theta)\) a la izquierda de ese punto (area por debajo de cero, es decir, por debajo del eje x, por supuesto, contando negativo). Para\(\theta=0\) esto debe ser exactamente 0.5 (ya que toda el área bajo se\(\delta_N(\theta)\) suma a 1). Pero si queremos el valor de\(f_N(\theta)\) at\(\theta=\pi/(2N+1)\) (es decir, el primer punto a la derecha del origen donde la curva corta a través del eje x), debemos sumar toda el área a la izquierda de\(\theta=\pi/(2N+1)\), lo que en realidad suma a un área total mayor que uno, ya que el área sobrante a la derecha de ese punto es negativa en general. Eso da el sobreimpulso.

Una serie de Fourier en Mecánica Cuántica: Electrón en una Caja

Las funciones de onda Schrödinger independientes del tiempo para un electrón en una caja (aquí un pozo cuadrado unidimensional con paredes infinitas) son solo las series de seno y coseno determinadas por las condiciones límite. Por lo tanto, cualquier función de onda inicial razonablemente suave que describa el electrón se puede representar como una serie de Fourier. El desarrollo del tiempo se puede encontrar multiplicando cada término de la serie por el factor de fase dependiente del tiempo apropiado.

Ejercicio\(\PageIndex{1}\)

Demostrar que para una función\(f(\theta)= \sum_{n=-\infty}^{\infty} a_n e^{in\theta} \), con el complejo\(a_n\) en general,

\[ \dfrac{1}{2\pi} \int\limits_{-\pi}^{\pi} |f(\theta)|^2 d\theta= \sum_{n=-\infty}^{\infty} |a_n|^2 \label{2.1.17}\]

La relevancia física de este resultado es la siguiente: para un electrón confinado a la circunferencia de un anillo de unidad de radio,\(\theta\) es la posición del electrón. Una base ortonormal de estados del electrón en este anillo es el conjunto de funciones\((1/\sqrt{2\pi})e^{in\theta}\) con\(n\) un entero, una superposición correctamente normalizada de estos estados debe tener\(\sum_{n=-\infty}^{\infty} |a_n|^2=1\), de manera que la probabilidad total de encontrar el electrón en algún estado es la unidad. Pero esto también debe significar que la probabilidad total de encontrar el electrón en cualquier parte del anillo es la unidad, y ese es el lado izquierdo de la ecuación anterior, la cancelación\(2\pi\) de la misma.

Serie Exponencial de Fourier

En la conferencia anterior, discutimos brevemente cómo un paquete de ondas gaussianas en el espacio x podría representarse como una superposición lineal continua de ondas planas que resultó ser otro paquete de ondas gaussianas, esta vez en k-espacio. El plan aquí es demostrar cómo podemos llegar a esa representación tomando cuidadosamente el límite de la serie bien definida de Fourier, pasando del intervalo finito\((-\pi,\pi)\) a toda la línea, y delinear algunos de los problemas matemáticos que surgen, y cómo manejarlos.

El primer paso es trivial: necesitamos generalizar de funciones reales a funciones complejas, para incluir funciones de onda que tengan corriente no desaparecida. Una función compleja suave se puede escribir en una serie de Fourier simplemente permitiendo\(A_n\) y\(B_n\) ser compleja, pero en este caso una expansión más natural sería en potencias de\(e^{i\theta},e^{-i\theta}\)

Escribimos:

\[f(\theta)=\sum_{n=-\infty}^{\infty}a_ne^{in\theta}\;\; with\;\; a_n=\dfrac{1}{2\pi}\int\limits_{-\pi}^{\pi}e^{-in\theta'} f(\theta')d\theta' \label{2.1.18}\]

y retrocediendo los pasos anteriores\[ f_N(\theta)=\dfrac{1}{2\pi}\int\limits_{-\pi}^{\pi}\sum_{n=-N}^{N}e^{in(\theta-\theta')}f(\theta')d\theta'=\dfrac{1}{2\pi}\int\limits_{-\pi}^{\pi} f(\theta')d\theta' +\dfrac{1}{\pi}\int\limits_{-\pi}^{\pi}\sum_{n=1}^{N}\cos n(\theta-\theta')f(\theta')d\theta' \label{2.1.19}\]

exactamente la misma expresión que antes, por lo tanto dando la misma\(\delta_N(\theta)\). Esto no es sorprendente, porque usar\(\cos n\theta=\dfrac{1}{2}(e^{in\theta}+e^{-in\theta}),\:\sin n\theta=\dfrac{1}{2i}(e^{in\theta}-e^{-in\theta})\) los primeros\(N\) términos en simplemente se\(A_n,\; B_n\) puede reorganizar a una suma sobre\(e^{in\theta}\) términos para\(-N\le n\le N\).

Electrón fuera de la caja: la Transformada de Fourier

Para descomponer un paquete de ondas en sus componentes de onda plana, necesitamos extender el rango de integración desde el\((-\pi,\pi)\) utilizado anteriormente hasta\((-\infty,\infty)\). Esto lo hacemos primero reescalando de\((-\pi,\pi)\) a\((-L/2,L/2)\) y luego tomando el límite\(L\rightarrow\infty\).

Escalar el intervalo de\(2\pi\) a\(L\) (en la representación compleja) da:

\[f(x)=\sum_{n=-\infty}^{\infty}a_ne^{2\pi inx/L}\;\; where\;\; a_n=\dfrac{1}{L}\int\limits_{-L/2}^{L/2}f(x)e^{-2\pi inx/L}dx \label{2.1.20}\]

la suma en\(n\) estar sobre todos los enteros. Esta es una expresión para\(f (x)\) en términos de ondas planas\(e^{ikx}\) donde están\(k\) los permitidos\(2\pi n/L\), con\(n = 0, \pm 1, \pm 2, …\)

Volviendo los pasos anteriores en la derivación de la función\(\delta_N(x)\), encontramos que la función equivalente es\[ \delta_N^L(x)=\dfrac{1}{L} \left(1+2\sum_{n=1}^N \cos\dfrac{2\pi nx}{L} \right)=\dfrac{\sin((2N+1)\pi x/L)}{L\sin(\pi x/L)} \label{2.1.21}\]

Al estudiar la expresión de la derecha, es evidente que siempre\(N\) es mucho mayor que\(L\), este tiene el mismo comportamiento de pico en el origen\(\delta_N(x)\) que el que consideramos anteriormente. Pero nos interesa el límite\(L\rightarrow\infty\), y ahí —para fijo\(N\) — esta función\(\delta_N^L(x)\) es baja y plana.

Por lo tanto, debemos tomar el límite N yendo al infinito antes de tomar L yendo al infinito.

Esto es lo que hacemos en el resto de esta sección.

Siempre\(L\) que sea finito, todavía tenemos una serie de Fourier, que representa una función de periodo\(L\). Nuestro principal interés en tomar\(L\) infinito es que nos gustaría representar una función no periódica, por ejemplo un paquete de ondas localizadas, en términos de componentes de onda plana.

Supongamos que tenemos tal paquete de onda, digamos de longitud\(L_1\), con lo que queremos decir que la onda es exactamente cero fuera de un tramo del eje de longitud\(L_1\). ¿Por qué no simplemente expresarlo en términos de una serie infinita de\(N\) Fourier basada en algún intervalo grande\( (-L/2,L/2)\) siempre que la longitud del paquete de onda\(L_1\) esté completamente dentro de este intervalo? El punto es que tal análisis reproduciría con precisión el paquete de ondas dentro del intervalo, ¡pero la misma suma de ondas planas evaluadas sobre todo el eje x revelaría una cadena infinita de paquetes de ondas idénticos\(L\) separados! Esto no es lo que queremos.

Como preliminar para llevar\(L\) al infinito, escribamos los términos de onda plana exponencial en la\(k\) notación estándar,

\[ e^{2\pi inx/L}=e^{ik_nx} \label{2.1.22}\]

Así que estamos sumando sobre un conjunto (infinito\(N\)) de ondas planas que tienen valores de número de onda

\[ k_n=2\pi n/L \; ,\; n = 0, \pm 1, \pm 2, … \label{2.1.23}\],

un conjunto de equidistantes\(k\) con separación\(\Delta k=2\pi/L\).

Consideremos ahora qué pasa si duplicamos el intervalo básico de\((-L/2,L/2)\) a\((-L,L)\).

Los nuevos\(k\) valores permitidos son\(k_n=\pi n/L \; ,\; n = 0, \pm 1, \pm 2, …\), por lo que la separación es ahora\(\Delta k=\pi/L\), la mitad de lo que era antes. Es evidente que a medida que aumentamos\(L\), el espaciamiento entre\(k_n\) valores sucesivos se vuelve cada vez menor.

Volviendo al intervalo de longitud\(L\), escribiendo\(La_n=a(k_n), \; k_n=2\pi n/L\) tenemos

\[ f(x)=\sum_{n=-\infty}^{\infty} a_ne^{2\pi in x/L}=\dfrac{1}{L} \sum_{n=-\infty}^{\infty} a(k_n)e^{ik_nx} \label{2.1.24}\]

Recordemos que la integral de Riemann puede definirse por

\[ \int f(k)dk=\lim_{\Delta k\rightarrow 0}\sum f(k_n)\Delta k \label{2.1.25}\]

con\(k_n=n\Delta k \; ,\; n = 0, \pm 1, \pm 2, …\).

La expresión en el lado derecho de la ecuación para\(f(x)\) tiene la misma forma que el lado derecho de la definición integral de Riemann, y aquí\(\Delta k=2\pi/L\).

Es decir,\[2\pi f(x)=\dfrac{2\pi}{L}\sum_{n=-\infty}^{\infty} a(k_n) e^{ik_nx}=\sum_{n=-\infty}^{\infty} a(k_n) e^{ik_nx}\Delta k=\int\limits_{-\infty}^{\infty} a(k)e^{ikx}dk \label{2.1.26}\]

en el límite\(\Delta k\rightarrow 0\), o equivalentemente\(L\rightarrow\infty\). Por supuesto, estamos asumiendo aquí que la función\(a(k_n)\), que solo hemos definido (para un dado\(L\)) en el conjunto de puntos\(k_n\), tiende a una función continua\(a(k)\) en el límite\(L\rightarrow\infty\).

De ello se deduce que en el\(L\) límite infinito, tenemos las ecuaciones de transformada de Fourier:

\[ f(x)=\dfrac{1}{2\pi}\int\limits_{-\infty}^{\infty} a(k)e^{ikx}dk \;\; and \;\; a(k)=\lim_{L\rightarrow \infty} La_n=\lim_{L\rightarrow \infty}\int\limits_{-L/2}^{L/2} f(x)e^{-2\pi inx/L}dx=\int\limits_{-\infty}^{\infty} f(x)e^{-ikx}dx \label{2.1.27}\]

Función Delta de Dirac

Ahora hemos llevado las dos\(N\) y\(L\) hasta el infinito, ¿qué ha pasado con nuestra función\(\delta_N^L(x)\)? Recuerde que nuestro procedimiento para encontrar\(f_N(\theta)\) en términos de\(f(\theta)\) dio la ecuación

\[f_N(\theta)=\dfrac{1}{2\pi} \int\limits_{-\pi}^{\pi} f(\theta') d\theta' +\dfrac{1}{\pi} \int\limits_{-\pi}^{\pi} \sum_{n=1}^{N} \cos n(\theta-\theta')f(\theta')d\theta' \label{2.1.10} \]

y de esto nos encontramos\(\delta_N(\theta)\).

Siguiendo el mismo procedimiento formal con las transformaciones de\((L=\infty)\) Fourier, nos vemos obligados a tomar\(N\) infinito (recordar el procedimiento solo tenía sentido si antes\(N\) se tomaba al infinito\(L\)), así que en lugar de una ecuación para\(f_N(\theta)\) en términos de\(f(\theta)\), obtenemos una ecuación para \(f (x)\)en términos de sí mismo! Anotémoslo primero y pensemos después:

\[f(x)=\dfrac{1}{2\pi}\int\limits_{-\infty}^{\infty} \left( \int\limits_{-\infty}^{\infty} f(x')e^{-ikx'}dx' \right) e^{ikx}dk=\int\limits_{-\infty}^{\infty} \left( \int\limits_{-\infty}^{\infty} \dfrac{dk}{2\pi}e^{ik(x-x')} \right) f(x')dx' \label{2.1.28}\]

En otras palabras,\[ f(x)= \int\limits_{-\infty}^{\infty} \delta(x-x')f(x')dx' \label{2.1.29}\]

donde\[ \delta(x)=\int\limits_{-\infty}^{+\infty} \dfrac{dk}{2\pi}e^{ikx} \label{2.1.30}\]

Esta es la función delta de Dirac. Este enfoque de saludar las manos ha dado un resultado que no está claramente definido. Esta integral sobre x es linealmente divergente en el origen, y tiene un comportamiento oscilatorio finito en todas partes. Para hacer algún progreso, debemos proporcionar alguna forma de corte en el espacio k, entonces tal vez podamos encontrar un límite significativo colocando el corte cada vez más lejos.

A partir de nuestros argumentos anteriores, deberíamos poder recuperarnos\(\delta(x)\) como límite de\(\delta_N^L(x)\) tomando primero\(N\) al infinito, luego\(L\). Es decir,

\[\delta(x)=\lim_{L\rightarrow\infty}\left(\lim_{N\rightarrow\infty}\delta_N^L(x)\right) =\lim_{L\rightarrow\infty}\left( \lim_{N\rightarrow\infty}\dfrac{\sin((2N+1)\pi x/L)}{L\sin(\pi x/L)} \right) \label{2.1.31}\]

Una manera de entender este límite es escribir\(M=(2N+1)\pi/L\) y dejar\(M\) ir al infinito antes\(L\). (Esto significa que a medida que tomamos\(L\) grandes en su camino hacia el infinito, ¡estamos tomando\(N\) mucho más grandes!)

Entonces el numerador es justo\(\sin Mx\). En el límite del infinito\(L\), para cualquier finito\(x\) el denominador es justo\(\pi x\), ya que\(\sin\theta =\theta\) en el límite de lo pequeño\(\theta\).

A partir de esto,

\[ \delta(x)=\lim_{M\rightarrow\infty} \dfrac{\sin Mx}{\pi x} \label{2.1.32}\]

Esta sigue siendo una función bastante patológica, en el sentido de que va oscilando cada vez más rápidamente a medida que se toma el límite infinito. Esto proviene del corte abrupto en la suma a la frecuencia\(N\).

Para ver cómo se relaciona esto con el (también mal definido)\(\delta(x)=\int\limits_{-\infty}^{+\infty}(dk/2\pi)e^{ikx}\), el recuerdo\(\delta_N^L(x)\) vino de la serie

\[ \delta_N^L(x)=\dfrac{\sin(2N+1)\pi x/L}{L\sin\pi x/L}=\dfrac{1}{L}\left( 1+2\sum_{n=1}^N \cos\dfrac{2\pi nx}{L} \right) \label{2.1.33}\]

Expresando el coseno en términos de exponenciales, luego reemplazando la suma por una integral en el\(N\) límite grande, de la misma manera que lo hicimos antes, escribiendo\(k_n=2\pi n/L\), así que el intervalo entre sucesivos\(k_n\) es\(\Delta k=2\pi/L\), así\(\int f(k)dk\ \cong (2\pi/L)\sum f(k_n)\):

\[ \delta_N^L(x)=\dfrac{1}{L}\sum_{n=-N}^N e^{2\pi in/L} \cong \int\limits_{-2\pi N/L}^{2\pi N/L}\dfrac{dk}{2\pi}e^{ikx} =\dfrac{\sin (2\pi Nx/L)}{\pi x} \label{2.1.34}\]

Entonces es claro que estamos definiendo el\(\delta(x)\) como un límite de la integral\(\int\limits_{-2\pi N/L}^{2\pi N/L}(dk/2\pi)e^{ikx}\), que se corta abruptamente a los valores grandes\(\pm (2\pi N/L)\). De hecho, esto no es muy físico: un escenario mucho más realista para un paquete de onda real sería una disminución gradual en las contribuciones de modos de alta frecuencia (o longitud de onda corta), es decir, un corte suave en la integral sobre el\(k\) que se utilizó para reemplazar la suma sobre\(n\). Por ejemplo, un procedimiento de corte razonable sería multiplicar el integrando por\(exp(-\Delta^2k^2)\), luego tomar el límite de pequeño\(\Delta\).

Por lo tanto, una definición más razonable de la función delta, desde el punto de vista de un físico, sería

\[ \delta(x)=\lim_{\Delta\rightarrow 0}\int\limits_{-\infty}^{\infty}\dfrac{dk}{2\pi}e^{ikx}e^{-\Delta^2 k^2}=\lim_{\Delta\rightarrow 0} \dfrac{1}{(4\pi\Delta^2)^{1/2}}e^{-x^2/4\Delta^2}=\lim_{\Delta\rightarrow 0} \delta_{\Delta}(x) \label{2.1.35}\]

Es decir, la función delta puede definirse como el “límite estrecho” de un paquete de onda gaussiana con área total 1. A diferencia de la función\(\delta_N(\theta)\), no\(\delta_{\Delta}(x)\) tiene bandas laterales oscilantes, gracias a nuestro alisado del punto de corte superior k-espacio, por lo que las discontinuidades escalonadas no generan el fenómeno de Gibbs' overshoot; en cambio, un paso se suavizará a lo largo de una distancia de orden\(\Delta\).

Propiedades de la función Delta

Es sencillo verificar las siguientes propiedades a partir de la definición como límite de un paquete de ondas gaussianas:

\[ \int \delta(x)dx=1, \; \delta(x)=0 \; for \; x\neq 0 \label{2.1.36}\]

\[ \delta(x)=\delta(-x), \; \delta(ax)=\dfrac{1}{|a|}\delta(x) \label{2.1.37}\]

\[ \int \delta(a-x)\delta(x-b)dx=\delta(a-b) \label{2.1.38}\]

Otra definición más, y una conexión con la Integral de Valor Principal

No hay una manera única de definir la función delta, y otros procedimientos de corte pueden proporcionar información útil. Por ejemplo, la integral k-espacio se puede dividir en dos y se pueden aplicar cortes exponenciales simples a las dos mitades, es decir, podríamos tomar la definición para ser\[ \delta(x)= \lim_{\varepsilon\rightarrow 0}\left( \int\limits_{-\infty}^{0}\dfrac{dk}{2\pi}e^{ikx}e^{\varepsilon k}+\int\limits_{0}^{\infty}\dfrac{dk}{2\pi}e^{ikx}e^{-\varepsilon k} \right) \label{2.1.39}\]

Evaluando las integrales,

\[ \delta(x)=\lim_{\varepsilon\rightarrow 0}\dfrac{1}{2\pi} \left(\dfrac{1}{ix+\varepsilon}-\dfrac{1}{ix-\varepsilon}\right)=\lim_{\varepsilon\rightarrow 0}\dfrac{1}{\pi}\left(\dfrac{\varepsilon}{x^2+\varepsilon^2}\right) \label{2.1.40}\]

Es fácil comprobar que esta función se normaliza correctamente haciendo el cambio de variable\(x=\varepsilon\tan\theta\) e integrando de\(-\pi/2\) a\(\pi/2\). Esta representación de la función delta demostrará ser útil posteriormente. Tenga en cuenta que considerada como una función de una variable compleja, la función delta tiene dos polos en el eje imaginario puro en\(z=\pm i\varepsilon\).

La definición estándar de la integral de valor principal es:

\[ \int\limits_{-D}^{D}f(x)\dfrac{P}{x}dx=\lim_{z\rightarrow 0}\left(\int\limits_{-D}^{-z}\dfrac{f(x)}{x}dx+\int\limits_{z}^{D}\dfrac{f(x)}{x}dx\right) \label{2.1.41}\]

No es difícil ver que para una función diferenciable continua\(f(x)\) esto equivale a

\[ \int\limits_{-D}^{D}f(x)\dfrac{P}{x}dx=\lim_{z\rightarrow 0}\int\limits_{-D}^{D}f(x)\dfrac{x}{x^2+\varepsilon^2}dx \label{2.1.42}\]

Por lo tanto, el operador de valor principal puede escribirse simbólicamente:

\[\dfrac{P}{x}=\lim_{z\rightarrow 0}\dfrac{x}{x^2+\varepsilon^2}=\lim_{z\rightarrow 0}\dfrac{1}{2}\left(\dfrac{1}{x+i\varepsilon}+\dfrac{1}{x-i\varepsilon}\right) \label{2.1.43}\]

Armando esto con la representación similar de la función delta anterior, y tomando el límite de\(\varepsilon\rightarrow 0\) a entender, tenemos el resultado útil:

\[ \dfrac{1}{x\pm i\varepsilon}=\dfrac{P}{x}\mp i\pi\delta(x) \label{2.1.44}\]

Ejercicios

1. Demostrar el teorema de Parseval:\[ If \;\; f(x)=\int_{-\infty}^{\infty} \dfrac{dk}{2\pi}a(k)e^{ikx}, \;\; then\;\; \int_{-\infty}^{\infty}|f(x)|^2dx=\int_{-\infty}^{\infty} \dfrac{dk}{2\pi}|a(k)|^2. \label{2.1.45}\]

2. Demostrar la regla para la Transformada de Fourier de una convolución de dos funciones:

\[ If \;\; f(x)=\int_{-\infty}^{\infty} \dfrac{dk}{2\pi}a(k)e^{ikx},\;\; g(x)=\int_{-\infty}^{\infty} \dfrac{dk'}{2\pi}b(k')e^{ik'x},\;\; then\;\; \int_{-\infty}^{\infty} f(x-x')g(x')dx'=\int_{-\infty}^{\infty} \dfrac{dk}{2\pi}a(k)b(k)e^{ikx} \label{2.1.46}\]

Colaborador

• Michael Fowler (Beams Professor, Department of Physics, University of Virginia)