4.6: El átomo de hidrógeno

Factorizar el centro del movimiento de masas

El átomo de hidrógeno consiste en dos partículas, el protón y el electrón, interactuando a través del potencial de Coulomb\(V(\vec{r_1}-\vec{r_2})=e^2/r\), donde como de costumbre\(r=|\vec{r_1}-\vec{r_2}|\). Escribir las masas de las dos partículas como la ecuación de\(m_1, m_2\) Schrödinger para el átomo es:\[ \left( -\frac{\hbar^2}{2m_1}\vec{\nabla_1}^2-\frac{\hbar^2}{2m_2}\vec{\nabla_2}^2-\frac{e^2}{r}\right) \psi(\vec{r_1},\vec{r_2})=E\psi(\vec{r_1},\vec{r_2}). \label{4.6.1}\]

Pero no\(\vec{r_1},  \vec{r_2}\) son las variables de posición más naturales para describir este sistema: dado que el potencial depende únicamente de la posición relativa, una mejor elección se\(\vec{r}, \vec{R}\) define por:\[ \vec{r}=\vec{r_1}-\vec{r_2},\;\; \vec{R}=\frac{m_1\vec{r_1}+m_2\vec{r_2}}{m_1+m_2} \label{4.6.2}\]

así\(\vec{R}\) es el centro de masa del sistema. Es conveniente al mismo tiempo denotar la masa total por\(M=m_1+m_2\), y la masa reducida por\(m=\frac{m_1m_2}{m_1+m_2}\).

Transformándose de manera directa a las variables La ecuación de\(\vec{r},  \vec{R}\) Schrödinger se convierte\[ \left(-\frac{\hbar^2}{2M}\vec{\nabla_R}^2-\frac{\hbar^2}{2m}\vec{\nabla_r}^2-\frac{e^2}{r}\right)\psi(\vec{R}, \vec{r})=E\psi(\vec{R}, \vec{r}). \label{4.6.3}\]

Escribir la función de onda\[ \psi(\vec{R}, \vec{r})=\Psi(\vec{R})\psi(\vec{r}) \label{4.6.4}\]

podemos dividir la ecuación en dos:\[ \begin{matrix} \left( -\frac{\hbar^2}{2M}\vec{\nabla_R}^2\right) \Psi(\vec{R})=E_R\Psi(\vec{R}) \\ \left( -\frac{\hbar^2}{2m}\vec{\nabla_r}^2+V(\vec{r})\right) \psi(\vec{r})=Er\psi(\vec{r}) \end{matrix}\label{4.6.5}\]

y la energía total del sistema es\(E=E_R+E_r\). Tenga en cuenta que el movimiento del centro de masa es (por supuesto) solo el de una partícula libre, teniendo una solución de onda plana trivial. A partir de ahora, sólo nos ocuparemos del movimiento relativo de las partículas. Dado que el protón es mucho más pesado que el electrón, casi siempre ignoraremos la diferencia entre la masa electrónica y la masa reducida, pero cabe señalar que la diferencia es fácilmente detectable espectroscópicamente: por ejemplo, las líneas se desplazan si el protón es reemplazado por un deuterón (hidrógeno pesado).

Estamos listos para escribir la ecuación de Schrödinger para el átomo de hidrógeno, dejando caer los sufijos r en la segunda ecuación anterior y escribir\(\vec{\nabla}^2\) explícitamente en coordenadas esféricas:

\[ \begin{matrix} -\frac{\hbar^2}{2m}\left( \frac{1}{r^2}\frac{\partial}{\partial r}\left( r^2\frac{\partial\psi}{\partial r}\right) +\frac{1}{r^2 \sin\theta}\frac{\partial}{\partial\theta}\left( \sin\theta\frac{\partial\psi}{\partial\theta}\right) +\frac{1}{r^2\sin^2\theta}\frac{\partial^2\psi}{\partial\varphi^2}\right) -\frac{e^2}{r}\psi \\ =E\psi. \end{matrix} \label{4.6.6}\]

Factorización de la Dependencia Angular: la Ecuación Radial -\(R(r)\)

Dado que el potencial es esféricamente simétrico, el hamiltoniano\(H\) viaja con los operadores de momento angular\(L^2\),\(L_z\) por lo que podemos construir un conjunto común de eigenkets de los tres operadores\(H\),\(L^2\),\(L_z\). La dependencia angular de estos propios mercados es, por lo tanto, la de los\(Y^m_l\)'s, por lo que las soluciones deben ser de la forma

\[ \psi_{Elm}(r,\theta,\phi)=R_{Elm}(r)Y^m_l(\theta,\phi). \label{4.6.7}\]

Ahora bien, observe que en la ecuación de Schrödinger anterior, la parte angular de\(\vec{\nabla}^2\) es exactamente el operador diferencial\(L^2/2mr^2\), por lo que operar sobre\(\psi_{Elm}(r,\theta,\phi)=R_{Elm}(r)Y^m_l(\theta,\phi)\) ella dará\(\hbar^2l(l+1)/2mr^2\). El armónico esférico\(Y^m_l\) puede entonces ser cancelado desde los dos lados de la ecuación dejando:

\[ \begin{matrix} -\dfrac{\hbar^2}{2m}\left( \dfrac{1}{r^2}\dfrac{d}{dr}(r^2\dfrac{d}{dr})-\dfrac{l(l+1)}{r^2}\right) R_{El}(r)-\dfrac{e^2}{r}R_{El}(r) \\ =ER_{El}(r) \end{matrix} \label{4.6.8}\]

siendo ahora evidente de lo que\(R(r)\) no puede depender\(m\).

Las derivadas radiales simplifican si uno factoriza fuera\(1/r\) de la función\(R\), escribiendo

\[ R_{El}(r)=\dfrac{u(r)}{r} \label{4.6.9}\]

y suprimir temporalmente el\(E\) y\(l\) para reducir el desorden.

La ecuación se convierte en:

\[ -\dfrac{\hbar^2}{2m}\left( \dfrac{d^2}{dr^2}-\dfrac{l(l+1)}{r^2}\right) u(r)-\dfrac{e^2}{r}u(r)=Eu(r). \label{4.6.10}\]

Reorganizar,

\[ -\dfrac{\hbar^2}{2m}\dfrac{d^2u(r)}{dr^2}+\left( \dfrac{\hbar^2}{2m}\dfrac{l(l+1)}{r^2}-\dfrac{e^2}{r}\right) u(r)=Eu(r). \label{4.6.11A}\]

Tenga en cuenta que esto es lo mismo que la ecuación de Schrödinger para una partícula en una dimensión, restringida a\(r>0\), en un potencial (para\(l\neq 0\)) ir al infinito positivo en el origen, luego negativo y yendo a cero a grandes distancias, por lo que siempre tiene un mínimo para algunos positivos\(r\).

Nos interesan los estados encuadernados del sistema protón-electrón, por lo que\(E\) será una cantidad negativa. En grandes separaciones, la ecuación de onda se simplifica a

\[ -\dfrac{\hbar^2}{2m}\dfrac{d^2u(r)}{dr^2}\cong E u(r) (for\; large\; r) \label{4.6.11B}\]

teniendo soluciones aproximadas\(e^{\kappa r}\),\(e^{-\kappa r}\) donde\(\kappa =\sqrt{-2mE/\hbar^2}\). Los estados ligados que buscamos, por supuesto, tienen funciones de onda exponencialmente decrecientes a grandes distancias.

Ir a una variable adimensional

Para simplificar aún más la ecuación, introducimos la variable adimensional\[ \rho=\kappa r,\;\; \kappa =\sqrt{-2mE/\hbar^2} \label{4.6.12}\]

dando\[ \frac{d^2u(\rho)}{d\rho^2}=\left( 1-\frac{2\nu}{\rho}+\frac{l(l+1)}{\rho^2}\right) u(\rho) \label{4.6.13}\]

donde (por razones que se harán evidentes en breve) hemos introducido\(\nu\) definido por\[ 2\nu=e^2\kappa /E. \label{4.6.14}\]

Observe que en la transformación de\(r\) a la variable adimensional\(\rho\) el factor de escala\(\kappa\) depende de la energía, ¡así que será diferente para diferentes estados vinculados a energía!

Consideremos ahora el comportamiento de la función de onda cerca del origen. El término dominante para suficientemente pequeño\(\rho\) es el centrífugo, por lo que\[ \frac{d^2u(\rho)}{d\rho^2}\cong \frac{l(l+1)}{\rho^2}u(\rho) \label{4.6.15}\]

para lo cual las soluciones son\(u(\rho)\sim \rho^{-l}\),\(u(\rho)\sim \rho^{l+1}\). Como la función de onda no puede ser singular, elegimos la segunda.

Hemos establecido que la función de onda decae como\(e^{-\kappa r}=e^{-\rho}\) a grandes distancias, y va lo\(\rho^{l+1}\) más cerca del origen. Factorizando estos dos comportamientos asintóticos, definidos\(w(\rho)\) por\[ u(\rho)=e^{-\rho}\rho^{l+1}w(\rho). \label{4.6.16}\]

Es sencillo (si es tedioso) establecer que\(w(\rho)\) satisface la ecuación diferencial:\[ \rho\frac{d^2w(\rho)}{d\rho^2}+2(l+1-\rho)\frac{dw(\rho)}{d\rho}+2(\nu-(l+1))w(\rho)=0. \label{4.6.17}\]

Poner en una solución de serie de ensayos\( w(\rho)=\sum_{k=0}^{\infty}w_k\rho^k\) da una relación de recurrencia entre coeficientes sucesivos:\[ \frac{w_{k+1}}{w_k}=\frac{2(k+l+1-\nu)}{(k+1)(k+2(l+1))}. \label{4.6.18}\]

Para grandes valores de\(k\),\(w_{k+1}/w_k\to 2/k\), así\(w_k\sim 2^k/k!\) y por lo tanto\(w(\rho)\sim e^2\rho\). Esto significa que hemos encontrado la función de onda radial divergente\(u(\rho)\sim e^{\rho}\), que de hecho es el comportamiento correcto para los valores generales de la energía.

Para encontrar los estados ligados, debemos elegir energías de tal manera que la serie no sea infinita. Mientras la serie se detenga en alguna parte, la disminución exponencial eventualmente asumirá el control y producirá una función de onda finita (estado enlazado). Al igual que para el simple oscilador armónico, esto sólo puede suceder si para algunos\(k, w_{k+1}=0\). Inspeccionando la relación\(w_{k+1}/w_k\), evidentemente la condición para un estado encuadernado es que\[ \nu=n,\;\; an\; integer \label{4.6.19}\]

en cuyo caso la serie para\(w(\rho)\) termina en\(k=n-l-1\). A partir de ahora, ya que sabemos que para las funciones que nos interesan\(\nu\) es un entero, reemplazamos\(\nu\) por\(n\).

Para encontrar las energías de estos estados ligados, recordar\(2n=2\nu=e^2\kappa /E\) y\(\kappa =\sqrt{-2mE/\hbar^2}\), así\[ 4n^2=\frac{e^4\kappa_n^2}{E_n^2}=-\frac{e^4}{E_n^2}\frac{2mE_n}{\hbar^2}, \label{4.6.20}\]

por lo\[ E_n=-\frac{me^4}{2\hbar^2}\frac{1}{n^2}=-\frac{13.6}{n^2} ev = -\frac{1}{n^2} Rydberg. \label{4.6.21}\]

(Esto define al Rydberg, una unidad popular de energía en la física atómica).

Sorprendentemente, ¡esta es la misma serie de energías de estado ligadas encontradas por Bohr a partir de su modelo! Por supuesto, sería mejor que este fuera el caso, ya que la serie de energías que Bohr encontró correctamente contabilizaban las líneas espectrales emitidas por los átomos de hidrógeno calientes. Observe, sin embargo, que existen algunas diferencias importantes con el modelo de Bohr: la energía aquí está determinada en su totalidad por\(n\), llamado el número cuántico principal, pero, en contraste con el modelo de Bohr, no\(n\) es el momento angular. El verdadero estado fundamental del átomo de hidrógeno,\(n=1\), tiene un momento angular cero: ya que\(n=k+l+1\),\(n=1\) significa ambos\(l=0\) y\(k=0\). Por lo tanto, la función de onda del estado fundamental es esféricamente simétrica, y la función\(w(\rho)=w_0\) es solo una constante. Por lo tanto,\(u(\rho)=\rho e^{-\rho}w_0\) y la función de onda radial real es esta dividida por\(r\), y por supuesto adecuadamente normalizada.

Para escribir la función de onda en términos de\(r\), necesitamos encontrar\(\kappa\). Armando\(\rho=\kappa_n r\),\(\kappa_n=\sqrt{-2mE_n/\hbar^2}\) y\(E_n=-\frac{me^4}{2\hbar^2}\frac{1}{n^2}\),\[ \kappa_n=\sqrt{2m\frac{me^4}{2\hbar^2}\frac{1}{n^2}}/\hbar=\frac{me^2}{\hbar^2n}=\frac{1}{a_0n}, \label{4.6.22}\]

donde la longitud\[ a_0=\frac{\hbar^2}{me^2}=0.529\times 10^{-10}m. \label{4.6.23}\]

se llama el radio de Bohr: de hecho es el radio de la órbita más baja en el modelo de Bohr.

Ejercicio: comprobar esta última declaración.

Vale la pena señalar en este punto que los niveles de energía se pueden escribir en términos del radio de Bohr\(a_0\):\[ E_n=-\frac{e^2}{2a_0}\frac{1}{n^2}. \label{4.6.24}\]

(Esto en realidad es obvio: recuerde que las energías\(E_n\) son idénticas a las del modelo Bohr, en el que está el radio de la\(n^{th}\) órbita\(n^2a_0\), por lo que la energía potencial electrostática es\(-e^2/na_0\), etc.)

Pasando a los estados excitados: para\(n=2\), tenemos una opción: o bien la función radial\(w(\rho)\) puede tener un término, como antes, pero ahora el momento angular\(l=1\) (desde\(n=k+l+1\)); o\(w(\rho)\) puede tener dos términos (así\(k=1\)), y\(l=0\). Ambas opciones dan la misma energía, -0.25 Ry, ya que n es lo mismo, y la energía sólo depende de\(n\). De hecho, hay cuatro estados en esta energía, ya que\(l=1\) tiene estados con\(m=1, m=0\) y\(m=-1\), y\(l=0\) tiene el único estado\(m=0\). (Por el momento, no estamos contando el factor extra de 2 a partir de las dos posibles orientaciones de espín del electrón.)

Porque\(n=3\), hay 9 estados en total: da uno,\(l=1\) da 3 y\(l=2\) da 5\(m\) valores diferentes. De hecho, para el número cuántico principal\(n\) hay estados\(n^2\) degenerados. (\(n^2\)siendo la suma de los primeros enteros\(n\) impares.)

Los estados pueden ser mapeados, energía verticalmente, momento angular horizontalmente:

La energía\(E=-1/n^2\), los niveles están etiquetados\(nl\),\(n\) siendo el número cuántico principal y la notación tradicional para el momento angular\(l\) se da en la parte inferior del diagrama. Las dos flechas verticales rojas son las dos primeras transiciones de la serie espectroscópica de Balmer, cuatro líneas de las cuales dieron a Bohr la pista que llevó a su modelo. Las series correspondientes de transiciones al estado\(1s\) fundamental están en el ultravioleta, se les llama la serie Lyman.

Funciones de onda para algunos estados bajos

A partir de ahora, etiquetamos las funciones de onda con los números cuánticos\(\psi_{nlm}(r,\theta,\phi)\), por lo que el estado fundamental es el esféricamente simétrico\(\psi_{100}(r)\).

Para este estado\(R(r)=u(r)/r\), donde\(u(\rho)=e^{-\rho}\rho^{l+1}w(\rho)=e^{-\rho}\rho w_0\), con\(w_0\) una constante, y\(\rho=\kappa_1 r=r/a_0\).

Entonces, en función de\(r\),\(\psi_{100}(r)=Ne^{-r/a_0}\) con\(N\) una constante de normalización fácilmente evaluada:

\[ \psi_{100}(r)=\left( \frac{1}{\pi a^3_0}\right)^{1/2}e^{-r/a_0}. \label{4.6.25}\]

Para\(n=2, l=1\) la función\(w(\rho)\) sigue siendo un solo término, una constante, pero ahora\(u(\rho)=e^{-\rho}\rho^{l+1}w(\rho)=e^{-\rho}\rho^2w_0\), y, para\(n=2\)\(\rho=\kappa r=r/2a_0\), recordar la dependencia energética de\(\kappa\).

Por lo tanto\(\psi_{210}(r,\theta,\phi)=N\left( \frac{r}{a_0}\right) e^{-r/2a_0}\cos\theta\). Nuevamente, evaluar la constante de normalización es rutinaria, cediendo\[ \psi_{210}(r,\theta,\phi)=\left( \frac{1}{32\pi a^3_0}\right)^{1/2}\left( \frac{r}{a_0}\right) e^{-r/2a_0}\cos\theta. \label{4.6.26}\]

Las funciones de onda para los otros\(m\) -valores\(\psi_{21\pm 1}(r,\theta,\phi)\),, tienen el\(\cos\theta\) in\(\psi_{210}\) reemplazado por\(\mp (1/\sqrt{2})\sin\theta e^{\pm i\phi}\) respectivamente (de la discusión anterior de los\(Y^m_l\)'s).

El otro\(n=2\) estado tiene\(l=0\), entonces de\(n=k+l+1\), tenemos\(k=1\) y la serie para\(w\) tiene dos términos,\(k=0\) y\(k=1\), siendo la proporción

\[ \frac{w_{k+1}}{w_k}=\frac{2(k+l+1-n)}{(k+1)(k+2(l+1))}=-1 \label{4.6.27}\]

para los valores relevantes:\(k=0, l=0, n=2\). Entonces\(w_1=-w_0\),\(w(\rho)=w_0(1-\rho)\). Para\(n=2\),\(\rho=r/2a_0\), la función de onda normalizada es

\[ \psi_{200}(r)=\left( \frac{1}{32\pi a^3_0}\right)^{1/2}\left( 2-\frac{r}{a_0}\right) e^{-r/2a_0}. \label{4.6.28}\]

Tenga en cuenta que las funciones de onda de momento angular cero son distintas de cero y tienen pendiente distinta de cero en el origen. ¡Esto significa que las funciones de onda tridimensional completas tienen una discontinuidad de pendiente allí! Pero esto está bien —el potencial es infinito en su origen. (En realidad, el protón no es una carga puntual, así que realmente la torcedura se suavizará sobre un volumen del tamaño del protón, un efecto muy pequeño).

Solución General de la Ecuación Radial

En la práctica, las primeras funciones radiales se\(w(\rho)\) pueden construir con bastante facilidad utilizando el método presentado anteriormente, pero cabe señalar que la ecuación diferencial para\(w(\rho)\)\[ \rho \frac{d^2w(\rho)}{d\rho^2}+2(l+1-\rho)\frac{dw(\rho)}{d\rho}+2(n-(l+1))w(\rho)=0 \label{4.6.29}\]

es de hecho la ecuación de Laplace, generalmente escrita\[ \left( z\frac{d^2}{dz^2}+(k-1-z)\frac{d}{dz}+p\right) L^k_p(z)=0 \label{4.6.30}\]

donde\(k,p\) están enteros, y\(L^k_p(z)\) es un polinomio de Laguerre (Mesías, página 482).

Las dos ecuaciones son las mismas si\(z = 2\rho\), y la solución a la ecuación radial es por lo tanto\[ w_{nl}(\rho)=L^{2l+1}_{n-l-1}(2\rho). \label{4.6.31}\]

Citando al Mesías, los polinomios\(L^0_p(z)\) de Laguerre y los polinomios asociados de Laguerre\(L^k_p(z)\) están dados por:

\[ \begin{matrix} L^0_p(z)=e^z\frac{d^p}{dz^p}e^{-z}z^p \\ L^k_p(z)=(-1)^k\frac{d^k}{dz^k}L^0_{p+k}(z). \end{matrix} \label{4.6.32}\]

(Estas representaciones se pueden encontrar ordenadamente resolviendo la ecuación de Laplace usando —sorpresa— una transformación de Laplace. Ver Merzbacher para más detalles.) Los polinomios satisfacen las relaciones de ortonormalidad (con la convención de normalización de los matemáticos)

\[ \int^{\infty}_{0}e^{-z}z^k L^k_p L^k_qdz=\frac{[(p+k)!]^3}{p!}\delta_{pq}. \label{4.6.33}\]

Pero, ¿cómo se ven? La función\(e^{-z}z^p\) es cero en el origen (aparte del caso trivial\(p=0\)) y cero en el infinito, siempre positiva y teniendo pendiente distinta de cero excepto en su valor máximo,\(z=p\). Las\(p\) derivadas traen ceros\(p\) separados, fácilmente comprobados dibujando las curvas generadas por diferenciación sucesiva. Por lo tanto\(L^0_p(z)\), un polinomio de grado\(p\), tiene ceros positivos\(p\) reales, y valor en el origen\(L^0_p(0)=p!\), ya que el único término distinto de cero a\(z=0\) es el generado por todos los operadores\(p\) diferenciales que actúan sobre él\(z^p\).

El polinomio Laguerre asociado\(L^k_p(z)\) se genera diferenciando\(L^0_{p+k}(z)\)\(k\) tiempos. Ahora\(L^0_{p+k}(z)\) tiene ceros positivos\(p+k\) reales, diferenciándolo da un polinomio un grado menor, con ceros que deben ser uno en cada intervalo entre los ceros de\(L^0_{p+k}(z)\). Este argumento sigue siendo válido para diferenciaciones sucesivas, por lo que\(L^k_p(z)\) deben tener ceros separados\(p\) reales.

Armando todo esto, y trasladando de\(\rho\) a\(r\), las soluciones radiales son:

\[ R_{nl}(r)=Ne^{-r/na_0}(\frac{r}{na_0})^l L^{2l+1}_{n-l-1}(\frac{2r}{na_0}) \label{4.6.34}\]

con\(N\) la constante de normalización. Griffiths (página 141) da más detalles, incluyendo las constantes de normalización elaboradas. Los usamos para trazar los\(n=3\) estados, trazando aquí las funciones\(u(r)=rR(r)\), ya que la normalización es\(4\pi \int^{\infty}_{0}|u(r)|^2dr=1, u(r)\) da una mejor idea de a qué distancia del protón es más probable que se encuentre el electrón.

Aquí están las tres funciones de onda\(n=3\) radial:

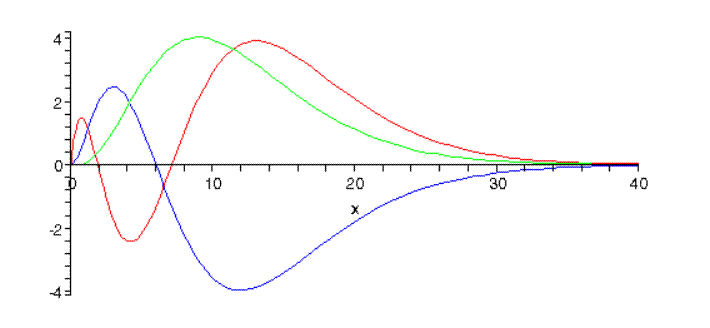
El número de nodos, el número cuántico radial, es\(3-l-1\). (Nota: Las normalizaciones relativas son correctas aquí, pero no la normalización general.)

Para\(n\) valores más altos, las funciones de onda se vuelven una reminiscencia de la mecánica clásica. por ejemplo, para\(n=10\), los picos de distribución de probabilidad de estado de momento angular más altos en\(r=100a_0\), el radio de órbita de Bohr:

mientras que para\(n=10, l=0\), encontramos:

Observe que este pico justo por debajo del doble del radio de Bohr. Esto se puede entender a partir de la mecánica clásica: para una ley de fuerza cuadrada inversa, las órbitas elípticas con el mismo eje semimajor tienen la misma energía. La\(l=n-1\) órbita es un círculo, la\(l=0\) órbita es una elipse larga y delgada (un extremo cercano al protón), por lo que se extiende casi el doble de distancia del origen que el círculo. Además, el electrón orbitante pasará más tiempo a la distancia lejana, ya que se irá moviendo muy lentamente. (Nota: las normalizaciones en las gráficas anteriores son sólo aproximadas.)