4.7: Adición de Momenta Angular

Considera un sistema que tiene dos momentos angulares, por ejemplo un electrón en un átomo de hidrógeno que tiene tanto momento angular orbital como espín. El espacio ket para un solo momento angular tiene una base ortonormal,\(|j,m\rangle\) por lo que para dos momentos angulares una base ortonormal obvia es el conjunto de kets de productos directos\(|j_1,m_1\rangle \otimes |j_2,m_2\rangle\). ¿Qué significa esto exactamente? Supongamos que el primer momento angular\(\vec{J}_1\) tiene magnitud\(\vec{J}^2_1=\hbar^2j_1(j_1+1)\), y está en el estado\(\sum_{m_1=-j_1}^{j_1}\alpha_{m_1}|j_1,m_1\rangle\), y de manera similar el segundo momento angular\(\vec{J}_2\) está en el estado\(\sum_{m_2=-j_2}^{j_2}\beta_{m_2}|j_2,m_2\rangle\). Evidentemente la amplitud de probabilidad para encontrar el primer giro en estado\(m_1\) y al mismo tiempo el segundo en\(m_2\) es\(\alpha_{m_1}\beta_{m_2}\), y denotamos ese estado por\(|j_1,m_1\rangle \otimes |j_2,m_2\rangle\). La forma de manejar estos espacios directos de productos quedará claro al examinar ejemplos específicos, como lo hacemos a continuación, comenzando con dos giros a la mitad.

Ahora la suma de dos momentos angulares\(\vec{J}=\vec{J}_1+\vec{J}_2\) es en sí misma un momento angular, operando en un espacio con una base completa\(|j,m\rangle\). Esto es fácil de probar: los componentes de\(\vec{J}_1\) satisfacer\([J_{1i},J_{1j}]=i\hbar \varepsilon_{ijk}J_{1k}\), y de manera similar para los componentes de\(\vec{J}_2\). Los componentes de\(\vec{J}_1\) desplazamiento con los componentes de\(\vec{J}_2\), por supuesto, de lo que se deduce inmediatamente que los componentes vectoriales de\(\vec{J}=\vec{J}_1+\vec{J}_2\) sí obedecen las relaciones de conmutación de momento angular: y recordar que las relaciones de conmutación fueron suficientes para determinar los conjuntos permitidos de valores propios. Demostraremos posteriormente que los estados propios\(|j,m\rangle\) de\(\vec{J}^2,\vec{J}_z\) son una base completa para el espacio de producto de los propios mercados de\(\vec{J}^2_1,\; \vec{J}^2_2,\; J_{1z},\; J_{2z}\) —para establecer esto, primero debemos encontrar los posibles valores permitidos del número cuántico de momento angular total\(j\).

Aquí tenemos, entonces, dos bases ortonormales diferentes para lo que evidentemente es el mismo espacio vectorial. En aplicaciones prácticas, muchas veces resulta que tenemos que traducir de una de estas bases a la otra. Nuestra tarea actual es construir la transformación adecuada: lo logramos encontrando los coeficientes de cualquiera\(|j,m\rangle\) en la\(|j_1,m_1\rangle \otimes |j_2,m_2\rangle\) base. A estos se les llama los coeficientes Clebsch-Gordan.

Vamos a construir gradualmente, comenzando por sumar dos giros un medio, luego un giro medio con un momento angular orbital, finalmente dos momentos angulares generales.

Agregar dos giros: los estados básicos y los operadores de giro

El ejemplo más elemental de un sistema que tiene dos momentos angulares es el átomo de hidrógeno en su estado fundamental. El momento angular orbital es cero, el electrón tiene un momento\(\frac{1}{2}\hbar\) angular de espín y el protón tiene giro\(\frac{1}{2}\hbar\).

El espacio de posibles estados del espín electrónico tiene los dos kets de base\(|\uparrow \rangle_e\) y\(|\downarrow \rangle_e\), (también escritos de diversas maneras como\(|+\rangle\),\(|-\rangle\);,;\(\dbinom{0}{1}\);\(\dbinom{1}{0}\)\(\chi +\),\(\chi -!\)) los kets de espín de protones de base son\(|\uparrow \rangle_p\) y\(|\downarrow \rangle_p\), por lo tanto, los estados posibles del combinado sistema son kets en el espacio directo del producto que tiene una base de cuatro kets:

\[ |\uparrow_e\uparrow_p\rangle ,\; |\uparrow_e\downarrow_p\rangle ,\; |\downarrow_e\uparrow_p\rangle ,\; |\downarrow_e\downarrow_p\rangle \label{4.7.1}\]

usando\(|\uparrow_e\uparrow_p\rangle\) como taquigrafía para\(|\uparrow \rangle_e\otimes |\uparrow \rangle_p\).

Observe aquí que hemos escrito los kets en “orden alfabético” con\(\uparrow\) como la primera letra,\(\downarrow\) como la segunda. Es decir, primero hemos escrito todas las kets teniendo\(\uparrow\) como primera letra, etc.

Para el caso más general de agregar\(j_1\) a\(j_2\), a considerar en breve, ordenaremos los kets de la misma manera “alfabéticamente”, escribiendo primero todos los kets que tengan\(m_1=j_1\), y así sucesivamente hasta\(m_1=-j_1\):

\[ (j_1j_2,j_1(j_2-1),\dots ,j_1(-j_2), (j_1-1)j_2,(j_1-1)(j_2-1),\dots ,(j_1-1)(-j_2),\dots ,(-j_1)(-j_2)). \label{4.7.2}\]

La dimensionalidad de este espacio es entonces\((2j_1+1)\times (2j_2+1)\).

Ahora el primer bloque de\(2j_2+1\) elementos tienen todos el mismo\(m\) - componente de\(j_1\), es decir\(m_1=j_1\), el siguiente bloque tiene\(m_1=j_1-1\), y así sucesivamente. Piense en lo que esto significa para construir un operador de rotación que actúe sobre los kets en este espacio: si opera solo en el momento angular\(j_1\), cambiará los factores\(m_1\) multiplicando los bloques, si el operador gira solo\(j_2\), operará dentro cada bloque, cambiándose todos los bloques de la misma manera.

Para tener una idea de cómo funciona esto en la práctica, volvemos al caso más simple, dos vueltas la mitad.

El espacio es de cuatro dimensiones, teniendo base\(|\uparrow_e\uparrow_p\rangle ,\; |\uparrow_e\downarrow_p\rangle ,\; |\downarrow_e\uparrow_p\rangle ,\; |\downarrow_e\downarrow_p\rangle\).

Cualquier operador que actúe sobre los giros estará representado por una\(4\times 4\) matriz, mejor pensada como una\(2\times 2\) matriz compuesta por\(2\times 2\) bloques: un operador que actúa sobre el giro de protones actúa dentro de los bloques, uno que opera sobre el espín electrónico afecta los factores multiplicadores generales frente a cada bloque.

Veamos algunos ejemplos. Recordemos que el operador de elevación para un solo giro es la\(2\times 2\) matriz\(S^+=\hbar\begin{pmatrix} 0&1 \\ 0&0 \end{pmatrix}\). Entonces, ¿cuál es el operador de elevación para el espín de electrones?

\[ S^+_e\otimes I_p=\hbar\begin{pmatrix} 0&I \\ 0&0 \end{pmatrix}=\hbar\begin{pmatrix} 0&0&1&0 \\ 0&0&0&1 \\ 0&0&0&0 \\ 0&0&0&0 \end{pmatrix}. \label{4.7.3}\]

Usamos negrita para denotar\(2\times 2\) matrices.

El patrón es claro: la estructura grande (en negrita arriba), la de los cuatro\(2\times 2\) bloques, refleja la estructura del operador de espín electrónico\(S^+=\hbar\begin{pmatrix} 0&1 \\ 0&0 \end{pmatrix}\), dentro de esos bloques (de los cuales solo uno sobrevive) el operador de identidad\(I=\begin{pmatrix} 1&0 \\ 0&1 \end{pmatrix}\) actúa sobre el espín de protones.

El operador que eleva el giro de protones es:\[ I_e\otimes S^+_p=\hbar \begin{pmatrix} \sigma^+&0\\ 0&\sigma^+ \end{pmatrix}=\hbar \begin{pmatrix} 0&1&0&0\\ 0&0&0&0\\ 0&0&0&1\\ 0&0&0&0 \end{pmatrix}. \label{4.7.4}\]

¿Qué pasa con el operador que eleva tanto el espín de electrones como de protones? En este caso, el patrón de bloques, y el patrón dentro de cada bloque, deben ser ambos\(\begin{pmatrix} 0&1 \\ 0&0 \end{pmatrix}\), así

\[ S^+_e\otimes S^+_p=\hbar^2\begin{pmatrix} 0&\sigma^+\\ 0&0 \end{pmatrix}=\hbar^2\begin{pmatrix} 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{pmatrix}. \label{4.7.5}\]

Sólo hay un elemento de matriz distinto de cero porque solo un miembro de la base sobrevive a esta operación.

Si dos giros interactúan (a través de sus momentos magnéticos, por ejemplo) de una manera que preserva el momento angular total, un posible término en el hamiltoniano sería\(S^-_eS^+_p\), representado por:

\[ S^-_eS^+_p=\hbar \begin{pmatrix} 0&0&0&0\\ 0&0&0&0\\ 0&1&0&0\\ 0&0&0&0 \end{pmatrix}=\hbar S^-_e\otimes S^+_p. \label{4.7.6}\]

Representando al Operador de Rotación para Dos Giros

Recordemos de la conferencia sobre giro que el operador de rotación en un solo giro la mitad es\[ D^{(1/2)}(R(\theta \hat{\vec{n}}))=e^{\frac{-i\theta \hat{\vec{n}}\cdot\vec{J}}{\hbar}} =e^{-i(\theta /2)(\hat{\vec{n}}\cdot \vec{\sigma})}=I\cos\frac{\theta}{2}-i(\hat{\vec{n}}\cdot \vec{\sigma})\sin\frac{\theta}{2} \label{4.7.7}\]

en el\(2\times 2\) giro o espacio. Como establecimos, este operador matricial tiene la forma\[ \begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}= \begin{pmatrix} \cos(\theta /2)-in_z\sin(\theta /2)&-(in_x+n_y)\sin(\theta /2)\\ (-in_x+n_y)\sin(\theta /2)&\cos(\theta /2)+in_z\sin(\theta /2) \end{pmatrix}. \label{4.7.8}\]

con\(|a|^2+|b|^2=1\).

Este conjunto de\(2\times 2\) matrices unitarias forman una representación del grupo de rotación en el sentido de que el total resultante de dos rotaciones sucesivas viene dado por la matriz que es el producto matriz de las correspondientes a las dos rotaciones.

De la discusión en la sección anterior, debe quedar claro que en el espacio de producto de los dos giros, la representación del operador de rotación —ambos giros por supuesto que experimentan la misma rotación— es:

\[ \begin{pmatrix} a\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}& b\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}\\ -b^*\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}& a^*\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix} \end{pmatrix}  = \begin{pmatrix} a^2&ab&ab&b^2\\ -ab^*&aa^*&-bb^*&a^*b\\ -ab^*&-bb^*&aa^*&a^*b\\ b^{*2}&-a^*b^*&-a^*b^*&a^{*2} \end{pmatrix}. \label{4.7.9}\]

Este conjunto de\(4\times 4\) matrices, de nuevo con\(|a|^2+|b|^2=1\), también debe formar una representación del grupo de rotación sobre el espacio de cuatro dimensiones. En breve descubriremos que esta representación puede simplificarse, pero para lograrlo necesitamos analizar los estados en términos de momento angular total.

Representación de Estados de Dos Giros en términos de Momentum Angular Total

Ahora estamos listos para analizar los estados de giro totales para el átomo de hidrógeno del estado fundamental (momento angular orbital cero).

Consideremos primero el estado con espín tanto de electrones como de protones apuntando hacia arriba,\(|\uparrow \uparrow \rangle\). El\(z\) - componente del giro total es\(S_z=S^e_z+S^p_z\), entonces\(S_z=\hbar\). Etiquetando el estado de giro total\(|s,m\rangle\), tenemos un estado con\(m=1\), entonces\(s=1\). (Para confirmar que este estado efectivamente tiene\(s=1\) podemos aplicar el operador de levantamiento de giro total\(S_+=S^e_+ +S^p_+\). Dado que ambos giros de componentes tienen\(m\) valor máximo\(S_+|s,1\rangle_{sm}=(S^e_+ +S^p_+)|\uparrow \uparrow \rangle =0\), pero\(S_+\) solo da cero cuando se actúa sobre el miembro m=s de un multiplete.)

Encontramos, entonces, que\(|\uparrow \uparrow \rangle =|1,1\rangle_{sm}\) donde hemos agregado el sufijo\(sm\) para dejar claro que los números en el último ket significan\(|s,m\rangle\) para el giro total. El giro total\(s=1\), al ser un estado propio de momento angular total, tiene un triplete de\(m\) valores\(m=1,0,-1\),\(|1,1\rangle_{sm}\) siendo el miembro superior. El\(m=0\) miembro se encuentra aplicando el operador de bajada a\(|\uparrow \uparrow \rangle\):

\[ S_-|\uparrow \uparrow \rangle =(S^e_-+S^p_-)(|\uparrow \rangle_e\otimes |\uparrow \rangle_p)=\hbar |\downarrow \rangle_e\otimes |\uparrow \rangle_p+\hbar |\uparrow \rangle_e\otimes |\downarrow \rangle_p \label{4.7.10}\]

que junto con

\[ S_-|\uparrow \uparrow \rangle =S_-|1,1\rangle_{sm}=\sqrt{2}\hbar |1,0\rangle_{sm}, \label{4.7.11}\]

da

\[ |1,0\rangle_{sm}=\frac{1}{\sqrt{2}}(|\downarrow \uparrow \rangle +|\uparrow \downarrow \rangle ). \label{4.7.12}\]

Obviamente, el tercer integrante del triplete,\(|1,-1\rangle_{sm}=|\downarrow \downarrow \rangle\).

Pero este triplete sólo da cuenta de tres estados base en la representación de momento angular\(|s,m\rangle\) total. Un cuarto estado, ortogonal a estos tres y normalizado, es\(\frac{1}{\sqrt{2}}(|\uparrow \downarrow \rangle -|\downarrow \uparrow \rangle )\). Esto tiene\(m=0\), y también tiene\(s=0\), fácilmente comprobado al señalar que el operador de elevación que actúa sobre este estado da cero, por lo que el estado tiene el máximo permitido\(m\) para su\(s\) valor.

Para resumir: en el momento angular total |s, m\ rangle representación para dos giros la mitad, los cuatro estados base son\(|1,1\rangle_{sm},\;  |1,0\rangle_{sm},\;  |1,-1\rangle_{sm},\;  |0,0\rangle_{sm}\). Esta base ortonormal abarca el mismo espacio que el otro conjunto ortonormal\(|\uparrow \uparrow \rangle ,\;  |\uparrow \downarrow \rangle ,\;  |\downarrow \uparrow \rangle ,\;  |\uparrow \uparrow \rangle\). Nuestra construcción de los\(|s,m\rangle\) estados anteriores equivale a encontrar un conjunto de kets básicos en términos de los demás.

Tenga en cuenta que dado que ambos conjuntos de kets base son ortonormales, mapear un vector de un conjunto a otro es una transformación unitaria. Pero hay más: los coeficientes que encontramos expresando una base ket en la otra base son todos reales. Esto quiere decir que si algún ket tiene coeficientes reales en una base, lo hace en la otra. Para este caso especial de todos los coeficientes reales, una transformación unitaria se llama ortogonal.

La transformación ortogonal que expresa una base en términos de la otra es fácil de construir:

\[ \begin{pmatrix} |1,1\rangle_{sm}\\ |1,0\rangle_{sm}\\ |0,0\rangle_{sm}\\ |1,-1\rangle_{sm} \end{pmatrix}=\begin{pmatrix} 1&0&0&0\\ 0&\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\ 0&\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0\\ 0&0&0&1 \end{pmatrix} \begin{pmatrix} |\uparrow \uparrow \rangle\\ |\uparrow \downarrow \rangle\\ |\downarrow \uparrow \rangle\\ |\downarrow \downarrow \rangle \end{pmatrix}. \label{4.7.13}\]

La matriz es ortogonal y simétrica, así es su propia inversa.

Geométricamente,\(s=1\) significa que los giros de los componentes son paralelos,\(s=0\) ya que son antiparalelos. Esto se puede afirmar con mayor precisión:\(2\vec{S}_1\cdot\vec{S}_2=S^2-S^2_1-S^2_2\), así para\(s=1\),\(\vec{S}_1\cdot\vec{S}_2=\frac{1}{2}\hbar^2\left( 2-\frac{3}{4}-\frac{3}{4}\right)=\hbar^2/4\), y para\(s=0\)\(\vec{S}_1\cdot\vec{S}_2=-\frac{3}{4}\hbar^2\). Esto facilita la construcción de operadores de proyección en los\(s=1\) subespacios\(s=0\) y:\(P_{s=1}=(\vec{S}_1\cdot\vec{S}_2/\hbar^2)+\frac{3}{4}\).

Ejemplo de física: un caso interesante de un sistema de dos espines es la molécula de hidrógeno. Los espines de electrones están en estado singlete (de lo contrario la molécula se disocia) pero los dos espines protónicos, que interactúan a través de sus momentos magnéticos) pueden ser paralelos (espín total uno), esto se llama ortohidrógeno, o antiparalelo (parahidrógeno). La diferencia de energía es suficientemente pequeña para que a temperatura ambiente la relación orto a para sea 3:1, lo que significa que todos los estados de espines son igualmente probables (efectivamente temperatura infinita), pero a temperaturas más bajas domina la forma para de menor energía. Esto es de hecho relevante para la tecnología de almacenamiento de hidrógeno líquido: la tasa de conversión de orto a para es muy lenta, pero cuando tiene lugar se libera energía. Si esto sucede después del almacenamiento, se requiere refrigeración adicional. Para evitar esto, se pueden usar catalizadores para apresurar la tasa de conversión durante el enfriamiento.

Representación del operador de rotación en la base de momento angular total

Ya hemos establecido que el operador de rotación, actuando sobre el sistema de dos espines, puede ser representado por una\(4\times 4\) matriz, y que la nueva base (momento angular total) puede alcanzarse desde la base original (dos giros separados) por la transformación ortogonal dada explícitamente anteriormente. Por lo tanto, la multiplicación previa y posterior del operador de rotación de dos giros dará de hecho una representación\(4\times 4\) matricial del operador de rotación en la nueva base de momento angular total.

Sin embargo, ese enfoque pierde el punto: primero, el estado singlete\(\frac{1}{\sqrt{2}}(|\uparrow \downarrow \rangle -|\downarrow \uparrow \rangle )\) tiene un momento angular cero, y así no se cambia por rotación.

Segundo, el estado triplete tiene un momento angular uno, por lo que los operadores de rotación deben actuar sobre él tal como encontramos anteriormente para un momento angular uno:\[ D^{(1)}(R(\vec{\theta}))=e^{\frac{-i\theta \hat{\vec{n}}\cdot\vec{J}}{\hbar}} =I+(\cos\theta -1)\left( \frac{\hat{\vec{n}}\cdot\vec{J}}{\hbar} \right)^2-i\sin\theta \left( \frac{\hat{\vec{n}}\cdot\vec{J}}{\hbar} \right). \label{4.7.14}\]

Esto significa que, en lo que respecta a las rotaciones, el espacio abarcado por los cuatro kets\(|0,0\rangle_{sm},\; |1,1\rangle_{sm},\; |1,0\rangle_{sm},\; |1,-1\rangle_{sm}\) es en realidad una suma de dos subespacios separados, el espacio unidimensional\(|0,0\rangle_{sm}\), y el espacio tridimensional que tiene base\(|1,1\rangle_{sm},\; |1,0\rangle_{sm},\; |1,-1\rangle_{sm}\). Bajo rotación, un vector en uno de estos subespacios permanece ahí: no hay términos cruzados en la matriz mezclando los espacios.

Esto significa que la matriz de rotación tiene la forma\(\begin{pmatrix} I&0\\ 0&R_3 \end{pmatrix}\) donde\(R_3\) está la\(3\times 3\) matriz para spin one,\(I\) es solo la matriz\(1\times 1\) trivial en el subespacio singlete, en otras palabras 1, y los\(0\) s son\(1\times 3\) y\(3\times 1\) conjuntos de ceros.

Un estado de los giros puede ser, por supuesto, una suma de componentes en los dos subespacios, por ejemplo

\[ |\uparrow \downarrow \rangle =\frac{1}{\sqrt{2}}\left( \frac{1}{\sqrt{2}}(|\uparrow \downarrow \rangle +|\downarrow \uparrow \rangle )+\frac{1}{\sqrt{2}}(|\uparrow \downarrow \rangle -|\downarrow \uparrow \rangle )\right). \label{4.7.15}\]

Representaciones grupales reducibles e irreducibles

Comenzamos nuestra discusión de dos giros a la mitad examinando las propiedades de los operadores de giro en el espacio de producto de cuatro dimensiones de los dos espacios de giro bidimensionales, y pasamos a construir una representación en cuatro dimensiones del operador de rotación general en ese espacio: una representación matricial de la rotación grupo. Pero cuando el sistema de dos espines se etiqueta en términos de momento angular total, encontramos que de hecho este operador de rotación de cuatro dimensiones es una suma de una rotación tridimensional, y una rotación de identidad trivial para un estado de momento angular cero. El operador de cuatro dimensiones puede ser “diagonalizado”: el espacio se divide en un espacio tridimensional y un espacio unidimensional que no se mezclan bajo rotación, y cualquier estado del sistema es una suma de kets de los dos espacios.

Esto a menudo se expresa diciendo que el espacio de producto de dos giros la mitad es la suma de un giro un espacio y un espacio de giro cero, y escrito\[ \frac{1}{2}\otimes \frac{1}{2}=1\oplus 0. \label{4.7.16}\]

Poniendo las dimensionalidades de los espacios en esta ecuación,\[ 2\times 2=3+1.\label{4.7.17}\]

Esta simple comprobación de la dimensionalidad total establece el patrón para espacios de producto más complicados que se examinan a continuación.

Se dice que la\(4\times 4\) representación del operador de rotación es una representación reducible: se puede reducir a una suma de representaciones dimensionales más pequeñas. Una representación irreducible es aquella en la que no hay subespacios invariantes bajo todas las rotaciones.

Recordemos que construimos la\(4\times 4\) representación reducible tomando un producto directo de las representaciones de mitad de\(2\times 2\) giro del grupo de rotación. La ecuación\(\frac{1}{2}\otimes \frac{1}{2}=1\oplus 0\) que usamos anteriormente para describir los espacios ket también se usa a menudo para describir las representaciones de grupos de rotación dentro de esos subespacios.

Uno podría preguntarse por qué nos molestaríamos en construir dos bases diferentes para el mismo espacio vectorial. La razón es que diferentes problemas necesitan diferentes bases. Para un sistema de dos giros en un campo magnético externo, no interactuando entre sí, la base de giros independientes\(|\uparrow \uparrow \rangle\), etc., es natural. Por otro lado, para un átomo de hidrógeno en ningún campo externo, pero incluyendo una interacción entre los espines (que están alineados con los momentos dipolares magnéticos de las partículas) la\(|j,m\rangle\) base es la correcta: la interacción hamiltoniana es proporcional a\(\vec{S}^e\cdot\vec{S}^p\) la que se puede escribir \(\frac{1}{2}(S^e_x+iS^e_y)(S^p_x-iS^p_y)+\frac{1}{2}(S^e_x-iS^e_y)(S^p_x+iS^p_y)+S^e_zS^p_z\), donde reconocemos a los operadores de subida y bajada para los giros individuales. Esto significa que el estado\(|\uparrow \downarrow \rangle\), por ejemplo, no puede ser un autoestado si el hamiltoniano incluye\(\vec{S}^e\cdot\vec{S}^p\), pero para este caso los estados\(|j,m\rangle\) son autoestados porque\(\vec{S}^e\cdot\vec{S}^p\) conmuta con el momento angular total y sus componentes.

Pero, ¿cuál sería una buena base para un átomo de hidrógeno, incluido el\(\vec{S}^e\cdot\vec{S}^p\) término, y en un campo magnético externo? Ese es un buen ejercicio para el lector.

Adición de un giro a un momento angular orbital

En esta sección, consideramos un átomo de hidrógeno en un estado con un momento angular orbital distinto de cero,\(\vec{L}\neq0\). Dicho movimiento orbital es equivalente a un bucle de corriente eléctrica y genera un campo magnético. El momento dipolar magnético asociado con el espín electrónico interactúa con este campo, teniendo el hamiltoniano apropiado un término proporcional a\(\vec{L}\cdot \vec{S}\), y se denomina interacción espín-órbita. El protón también tiene un momento magnético, pero eso es tres órdenes de magnitud menor que el del electrón, así que lo vamos a descuidar por ahora.

La interacción espín-órbita\(\vec{L}\cdot \vec{S}\) se analiza de forma más natural en los estados base del momento angular total\(|j,m\rangle\), donde\(\vec{J}=\vec{L}+\vec{S}\) (ver la discusión análoga de la interacción espín-espín anterior). Escriba los estados propios de momento angular orbitales\(|l,m_l\rangle\) y los estados de giro\(|s,m_s\rangle\) donde\(|\frac{1}{2},\frac{1}{2}\rangle =|\uparrow \rangle\) y\(|\frac{1}{2},-\frac{1}{2}\rangle =|\downarrow \rangle\). El espacio del producto\(|l,m_l\rangle \otimes |s,m_s\rangle\) es\(2(2l+1)\) dimensional: un solo ket en este espacio de producto sería completamente descrito por\(|l,m_l;s,m_s\rangle\), pero como ambos\(l,s\) son constantes a lo largo del problema, las únicas variables reales son\(m_l,m_s\) así que escribiremos el ket en la forma más compacta \(|m_l,m_s\rangle_{m_lm_s}\), por ejemplo\(|2,\frac{1}{2}\rangle_{m_lm_s}\).

El componente de momento angular máximo posible en la dirección z es claramente\((l+\frac{1}{2})\hbar\), para el estado\(|l,\frac{1}{2}\rangle_{m_1m_2}\). En la representación de momento angular total, este debe ser el estado\(|j,m\rangle =|l+\frac{1}{2},l+\frac{1}{2}\rangle_{jm}\). Entonces las dos bases diferentes tienen un miembro común:\[ |l+\frac{1}{2},l+\frac{1}{2}\rangle_{jm}=|l,\frac{1}{2}\rangle_{m_lm_s}. \label{4.7.18}\]

En la\(|j,m\rangle\) representación de momento angular total,\(|l+\frac{1}{2},l+\frac{1}{2}\rangle_{jm}\) es el\(m\) estado superior de un multiplete que tiene\(2(l+\frac{1}{2})+1=2l+2\) miembros. Al igual que para el caso de centrifugado, el siguiente miembro abajo del multiplete se genera aplicando el operador de bajada:\[ \begin{matrix} J_-|l+\frac{1}{2},l+\frac{1}{2}\rangle_{jm}=\sqrt{2l+1} \hbar |l+\frac{1}{2},l-\frac{1}{2}\rangle_{jm}\\ =(L_-+S_-)|l,\frac{1}{2}\rangle_{m_lm_s}\\ =\sqrt{2l} \hbar |l-1,\frac{1}{2}\rangle_{m_lm_s}+\hbar |l,-\frac{1}{2}\rangle_{m_lm_s} \end{matrix}. \label{4.7.19}\]

Por lo tanto\[ |l+\frac{1}{2},l-\frac{1}{2}\rangle_{jm}=\sqrt{\frac{2l}{2l+1}}|l-1,\frac{1}{2}\rangle_{m_lm_s}+\sqrt{\frac{1}{2l+1}}|l,-\frac{1}{2}\rangle_{m_lm_s}. \label{4.7.20}\]

Este estado\(|l+\frac{1}{2},l-\frac{1}{2}\rangle_{jm}\) se encuentra en el\(m=l-\frac{1}{2}\) subespacio, que es bidimensional, teniendo vectores de base\(|l-1,\frac{1}{2}\rangle_{m_lm_s}\) y\(|l,-\frac{1}{2}\rangle_{m_lm_s}\) en la\(|\rangle_{m_lm_s}\) representación. Por lo que también debe tener dos vectores base en la\(|\rangle_{jm}\) representación. El otro\(|\rangle_{jm}\) ket debe ser ortogonal\(|l+\frac{1}{2},l-\frac{1}{2}\rangle_{jm}\) y normalizado: solo puede ser\[ |l-\frac{1}{2},l-\frac{1}{2}\rangle_{jm}=\sqrt{\frac{2l}{2l+1}}|l,-\frac{1}{2}\rangle_{m_lm_s}-\sqrt{\frac{1}{2l+1}}|l-1,\frac{1}{2}\rangle_{m_lm_s}. \label{4.7.21}\]

Hemos representado a este nuevo ket\(|\rangle_{jm}\) como el estado superior de un\( j=l-\frac{1}{2}\) multiplete. Es fácil comprobar que este es efectivamente el caso: tiene\(m=l-\frac{1}{2}\), y\(J_+\) actuar sobre él da cero, por lo que tiene que ser el miembro superior de su multiplete. La única ambigüedad es una fase general: la convención Condon-Shortley es que al estado m más alto del momento angular del componente más grande se le asigna un coeficiente positivo.

Así\(|l-\frac{1}{2},l-\frac{1}{2}\rangle_{jm}\) es el estado superior de un nuevo multiplete que tiene\(2(l-\frac{1}{2})+1=2l\) miembros. Los dos multipletes\(j=l+\frac{1}{2}\) y\(j=l-\frac{1}{2}\) tomados juntos tienen\(2(2l+1)\) miembros, y por lo tanto abarcan todo el espacio\(2(2l+1)\) dimensional. El resto de los vectores\(|\rangle_{jm}\) base se generan mediante la aplicación repetida del operador de descenso en los dos multipletes.

La razón por la que solo hay dos multipletes en este problema es que solo hay dos formas en que el giro medio puede apuntar en relación con el momento angular orbital. Recordando que para los dos giros expresamos el espacio del producto una suma de un espacio de giro 1 y un espacio de giro 0\(\frac{1}{2}\otimes \frac{1}{2}=1\oplus 0\),, la ecuación análoga aquí es\[ \frac{1}{2}\otimes l=(l+\frac{1}{2})\oplus (l-\frac{1}{2}). \label{4.7.22}\]

Para el caso general de sumar momentos angulares\(j_1, j_2\) con\(j_1\ge j_2\), se generan\(2j_2+1\) multipletes, correspondientes al número de posibles orientaciones relativas de los dos momentos angulares.

Agregando Dos Momenta Angular: el Caso General

El espacio de kets que describen dos momentos angulares\(j_1, j_2\) es el producto directo de dos espacios cada uno para un solo momento angular, pero la naturaleza directa del producto de los kets generalmente no se hace explícita, se\(|j_1,m_1\rangle \otimes |j_2,m_2\rangle\) puede escribir como un solo ket\(|j_1,m_1;j_2,m_2\rangle\). Al igual que en los ejemplos anteriores, ya que\(j_1, j_2\) son fijos a lo largo, no es necesario que se escriban en cada ket, solo escribiremos\(|m_1,m_2\rangle\), o, cuando se trata de valores numéricos, agregaremos\(m_1m_2\) como sufijo:\(|2,3\rangle_{m_1m_2}\).

Los kets\(|m_1,m_2\rangle\) forman una base ortonormal completa del espacio\((2j_1+1)(2j_2+1)\) dimensional del producto de los dos momentos angulares: son los estados propios del conjunto completo de variables de desplazamiento\(\vec{J}_1^2,\;  J_{1z},\; \vec{J}^2_2, \; J_{2z}\).

Estados de base de momento angular total

Por supuesto, existe una base ortogonal completa alternativa del espacio de los dos momentos angulares: para el momento angular total\(\vec{J}=\vec{J}_1+\vec{J}_2\), un conjunto diferente de variables completas de desplazamiento es:\(\vec{J}_1^2,\; \vec{J}^2_2,\;  \vec{J}^2,\; J_z\). (Este no es el mismo conjunto de estados que en el párrafo anterior: por ejemplo,\(\vec{J}^2\) no conmuta con\(J_{1z}\). ¡Compruébalo!)

Este conjunto alternativo es un mejor conjunto de bases para dos momentos angulares que interactúan entre sí, un término de interacción como\(\vec{J}_1\cdot \vec{J}_2\) puede cambiar\(m_1, m_2\) pero no\(m=m_1+m_2\), o\(\vec{J}^2\).

Como siempre, estamos tomando como constantes\(\vec{J}_1^2,\; \vec{J}^2_2\) a lo largo, por lo que las variables significativas aquí son\(\vec{J}^2\) y\(J_z\), y escribimos los estados simplemente como\(|j,m\rangle\) o cuando tenemos valores numéricos,\(|3,1\rangle_{jm}\), siguiendo la notación introducida anteriormente. Por supuesto,\(\vec{J}^2|j,m \rangle =j(j+1)\hbar^2|j,m \rangle\), y\(J_z|j,m \rangle =m\hbar |j,m \rangle\).

Pasar de una base a otra: los coeficientes de Clebsch-Gordan

¿Cómo escribimos un estado\(|j,m\rangle\) en términos de los estados\(|m_1,m_2\rangle\)? Además, ¿cómo demostramos que el nuevo conjunto de estados\(|j,m\rangle\) es una base completa para el espacio?

Sabemos que el conjunto de estados\(|m_1,m_2\rangle\) es una base completa, ya que todo el espacio es un espacio de producto de los\(j_1\) y\(j_2\) espacios, los cuales son abarcados por los conjuntos\(|m_1\rangle\),\(|m_2\rangle\) respectivamente. Por lo tanto, el operador de identidad puede ser escrito\[ I=\sum_{m_1=-j_1}^{j_1}\sum_{m_2=-j_2}^{j_2}|m_1,m_2\rangle \langle m_1,m_2|. \label{4.7.23}\]

De ello se deduce que se\(|j,m\rangle\) puede expresar como una suma sobre los vectores base\(|m_1,m_2\rangle\):\[ |j,m\rangle=\sum_{m_1=-j_1}^{j_1}\sum_{m_2=-j_2}^{j_2}|m_1,m_2\rangle \langle m_1,m_2|j,m\rangle \label{4.7.24}\]

\(\langle m_1,m_2|j,m \rangle\)Los coeficientes se denominan coeficientes de Clebsch Gordan, a menudo los coeficientes CG escritos.

Una propiedad inmediata de los coeficientes CG es que\(\langle m_1,m_2|j,m \rangle =0\) a menos que\(m=m_1+m_2\). Esto se desprende de la identidad del operador\(J_z=J_{1z}+J_{2z}\) tomada entre un sostén y un ket de diferentes bases,\[ \langle m_1,m_2|J_z|j,m\rangle =\langle m_1,m_2|J_{1z}+J_{2z}|j,m\rangle \label{4.7.25}\]

y\[ J_z|j,m\rangle =m\hbar |j,m\rangle ,\; \langle m_1,m_2|(J_{1z}+J_{2z})=\langle m_1,m_2|(m_1+m_2)\hbar , \label{4.7.26}\]

entonces\[ (m-m_1-m_2)\langle m_1,m_2|j,m\rangle =0. \label{4.7.27}\]

Ya sabemos que el valor máximo de\(m_1\) es\(j_1\), y de\(m_2\) es\(j_2\), entonces el valor máximo de\(m\) es\(j_1+j_2\). Por lo tanto, el valor máximo de\(j=j_1+j_2\), porque si pudiera ir más alto, habría un mayor en\(m\) algún lugar del espacio, contradictorio\(m=m_1+m_2\).

Para el conjunto\(|m_1,m_2\rangle\), hay un ket que tiene este valor máximo de m:\(|j_1,j_2\rangle_{m_1m_2}\). Igualmente, en el conjunto de estados solo\(|j,m\rangle\) hay uno con el m máximo:\(|j_1+j_2, j_1+j_2\rangle_{jm}\). Por lo tanto, estos dos kets deben ser idénticos (estableciendo el factor de fase arbitrario igual a uno):\[ |j_1,j_2\rangle_{m_1m_2}=|j_1+j_2, j_1+j_2\rangle_{jm}. \label{4.7.28}\]

Ahora\(|j_1+j_2, j_1+j_2\rangle_{jm}\) es el ket superior en un multiplete que tiene\(2(j_1+j_2)+1\) miembros.

El miembro siguiente al principio del multiplete se genera como antes aplicando el operador de bajada a ambas representaciones:\[ J_-|j_1+j_2, j_1+j_2\rangle_{jm}=(J_{1-}+J_{2-})|j_1, j_2\rangle_{m_1m_2} \label{4.7.29}\]

dando\[ \sqrt{2(j_1+j_2)}\hbar |j_1+j_2, j_1+j_2-1\rangle_{jm}=\sqrt{2j_1}\hbar |j_1-1, j_2\rangle_{m_1m_2}+\sqrt{2j_2}\hbar |j_1, j_2-1\rangle_{m_1m_2} \label{4.7.30}\]

entonces\[ |j_1+j_2, j_1+j_2-1\rangle_{jm}=\sqrt{\frac{j_1}{j_1+j_2}}|j_1-1, j_2\rangle_{m_1m_2}+\sqrt{\frac{j_2}{j_1+j_2}}|j_1, j_2-1\rangle_{m_1m_2} \label{4.7.31}\]

y por analogía exacta con el caso de la órbita de espín, el otro estado\(|\rangle_{jm}\) base en el\(m=j_1+j_2-1\) subespacio es\[ |j_1+j_2-1, j_1+j_2-1\rangle_{jm}=-\sqrt{\frac{j_2}{j_1+j_2}}|j_1-1, j_2\rangle_{m_1m_2}+\sqrt{\frac{j_1}{j_1+j_2}}|j_1, j_2-1\rangle_{m_1m_2} \label{4.7.32}\]

con la convención de firma apropiada para\(j_1>j_2\). Este es el miembro superior de un multiplete que tiene\(j=j_1+j_2-1\), y así\(2(j_1+j_2-1)+1=2(j_1+j_2)-1\) miembros (comprobado como de costumbre aplicando\(J_+\) y obteniendo cero).

Para continuar, se aplica una vez más el operador de bajada, para ingresar al\(m=j_1+j_2-2\) subespacio. En la\(|\rangle_{m_1m_2}\) representación, esta tiene tres vectores de base independientes (proporcionados\(j_2>\frac{1}{2}\)):\(|j_1-2, j_2\rangle_{m_1m_2},\; |j_1-1, j_2-1\rangle_{m_1m_2},\; |j_1, j_2-2\rangle_{m_1m_2}\). Pero sólo se han bajado dos kets en la\(|\rangle_{jm}\) representación: el tercer\(|\rangle_{jm}\) ket faltante en el\(m=j_1+j_2-2\) subespacio debe ser el miembro superior de otro nuevo multiplete que tenga\(j=j_1+j_2-2\), y así\(2(j_1+j_2)-3\) miembros.

Tenga en cuenta que los coeficientes generados por los operadores de bajada son todos reales, por lo que los tres\(|\rangle_{jm}\) kets en el\(m=j_1+j_2-2\) subespacio pueden escribirse en términos de los\(|\rangle_{m_1m_2}\) kets con coeficientes reales.

Este proceso puede repetirse hasta que los\(|\rangle_{jm}\) multipletes generados abarquen el espacio. Recordemos que la dimensionalidad del espacio, desde la\(|\rangle_{m_1m_2}\) representación, es\((2j_1+1)(2j_2+1)\). Los multipletes se\(|\rangle_{jm}\) suman a una dimensionalidad total\[ 2(j_1+j_2)+1+2(j_1+j_2)-1+2(j_1+j_2)-3+\dots \label{4.7.33}\]

pero ¿dónde paramos? El sentido común sugiere que para\(j_1>j_2\), el momento angular total mínimo debe ser\(j=j_1-j_2\). El sentido común no es necesariamente de confiar, pero es claro que todos los miembros de los multipletes se\(|\rangle_{jm}\) generan mediante el uso del operador de bajada, seguido de la introducción de un nuevo miembro superior multiplete ortogonal cada vez, como se describió anteriormente, son kets ortonormales independientes, y si nos detenemos en \(j=j_1-j_2\), el número total generado es\[ \sum_{n=|j_1-j_2|}^{j_1+j_2} (2n+1)=(2j_1+1)(2j_2+1). \label{4.7.34}\]

(Uso\(\sum_{n=0}^{m}(2n+1)=(m+1)^2\).) Esto establece que incluir todos los momentos angulares totales entre\(|j_1-j_2|\) y de hecho\(j_1+j_2\) da una base completa que abarca el espacio, por lo que

\[ j_1\otimes j_2=(j_1+j_2)\oplus (j_1+j_2-1)\oplus \dots \oplus (|j_1-j_2|). \label{4.7.35}\]

Cálculo de coeficientes de Clebsch-Gordan mediante relaciones de recursión

El esquema presentado anteriormente, construyendo una sucesión de multipletes comenzando desde el estado m más alto y utilizando la convención Condon-Shortley para establecer signos, generará todos los coeficientes CG. Sin embargo, otro enfoque resulta útil en trabajos posteriores. Recordemos que al encontrar elementos matriciales de\(J_z=J_{1z}+J_{2z}\) entre un\(\langle m_1,m_2|\) sujetador y un\(|j,m\rangle\) ket, establecimos que los coeficientes de Clebsch-Gordan son cero a menos que\(m=m_1+m_2\). Una evaluación paralela de elementos matriciales de\(J_{\pm} =J_{1\pm} +J_{2\pm}\) rendimientos una relación entre tres coeficientes CG:\[ \langle m_1,m_2|J_+|j,m\rangle =\langle m_1,m_2|J_{1+}|j,m\rangle +\langle m_1,m_2|J_{2+}|j,m\rangle \label{4.7.36}\]

rendimientos\[ \begin{matrix} \sqrt{j(j+1)-m(m+1)}\langle m_1,m_2|j,m+1\rangle =\\ \sqrt{j_1(j_1+1)-m_1(m_1-1)} \langle m_1-1,m_2|j,m\rangle +\sqrt{j_2(j_2+1)-m_2(m_2-1)}\langle m_1,m_2-1|j,m\rangle \end{matrix} \label{4.7.37}\]

donde\(J_{1+}\) actuar a la izquierda se reduce\(m_1\) en uno. (Aquí, obviamente, debemos elegir\(m=m_1+m_2-1\) tener coeficientes distintos de cero.)

Para visualizar lo que está pasando con todos estos coeficientes, recuerde que\(m_1\) puede tomar\(2j_1+1\) valores y\(m_2\) puede tomar\(2j_2+1\) valores, así que dado\(j_1,j_2\) cada estado posible de los dos giros puede ser representado por un punto en una\((2j_1+1)\times (2j_2+1)\) cuadrícula: aquí está\(j_1=3,  j_2=2\):

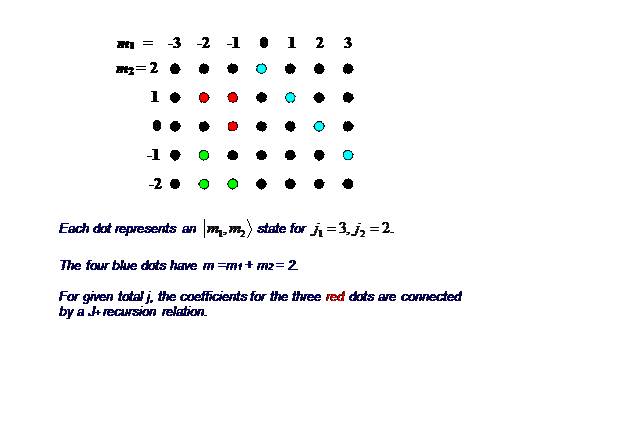
¿Cómo se relacionan estos puntos con los coeficientes CG? el punto superior derecho (3, 2) representa de manera única el\(j=5,\;  m=5\) estado del momento angular total. Los siguientes puntos hacia abajo, (2, 2) y (3, 1), corresponden a dos coeficientes CG para\(j=5\) y dos coeficientes CG diferentes para\(j=4\).

Si ahora elegimos un valor\(j\) menor que\(j_1+j_2\), cada punto de la cuadrícula corresponderá a un coeficiente.

Tenga en cuenta que habiendo arreglado\(j\), la cuadrícula se verá reducida: tomemos\(j=3\), así que\(m=m_1+m_2=3\) a lo sumo. Entonces la grilla pierde sus esquinas más lejanas:\[ |j_1,m_1\rangle \otimes |j_2,m_2\rangle. \label{4.7.38}\]

Examinemos para esto fijo\(j\) qué coeficientes CG están donde en esta cuadrícula reducida.

Hay un total de\(2j+1=7\) estados para\(m=3, 2 ,\dots ,-3\).

El estado superior\(j=3,\; m=3\), o\(|3,3\rangle_{jm}\), viene dado por tres coeficientes en la línea diagonal superior (está en un subespacio tridimensional, y ortogonal a\(j=5\) y miembros\(j=4\) multiplete\(|5,3\rangle_{jm}\),\(|4,3\rangle_{jm}\) que también están en el\(m=3\) subespacio). No estamos en este punto calculando estos coeficientes, solo estamos tratando de encontrarles un hogar.

Aplicando el operador de bajada a\(|3,3\rangle_{jm}\) da un vector en el\(m=2\) subespacio de cuatro dimensiones, los coeficientes pertenecerían a la siguiente diagonal hacia abajo, que tiene cuatro elementos. (Este subespacio también incluye el miembro superior del\(j=2\) multiplete.) Usando el operador de bajada una vez más ingresamos al\(m=1\) subespacio de cinco dimensiones, pero ese es el número máximo de dimensiones en este problema, ya que los momentos angulares 3 y 2 no se pueden agregar para dar un\(j=0\) escalar.

Teniendo ahora, para este particular\(j\) hecho a partir de\(j_1+j_2\), encontrado donde se encuentran todos los coeficientes CG para todos los miembros del\(2j+1\) multiplete, veremos cómo se pueden calcular todos sistemáticamente utilizando las relaciones de recursión generadas por\(J_{\pm} =J_{1\pm} +J_{2\pm}\).

Hemos mapeado las relaciones de recursión en el diagrama: dados\(j,\;  j_1,\;  j_2\) los tres puntos rojos en\((m_1,m_2),\;  (m_1-1,m_2),\;  (m_1,m_2-1)\) (con\(m_1=-1,\; m_2=1\) en este ejemplo) localizar los tres coeficientes CG que satisfacen la ecuación lineal anterior de\[ \langle m_1,m_2|J_+|j,m\rangle =\langle m_1,m_2|J_{1+}|j,m\rangle +\langle m_1,m_2|J_{2+}|j,m\rangle \label{4.7.39}\]

así que si se conocen dos de ellos se da el tercero. De igual manera, la ecuación paralela generada por\(J_-=J_{1-}+J_{2-}\) vincula los tres puntos verdes, at\((m_1,m_2),\;  (m_1+1,m_2),\;  (m_1,m_2+1)\).

Comenzamos el cálculo de los coeficientes CG con el punto azul, el punto en los bordes iniciales de “flecha”. Asignemos arbitrariamente un valor 1 a este punto. Si lo hacemos el miembro superior de un triángulo “verde”, eso lo vinculará al punto de abajo y a un punto a la derecha que está fuera de la matriz. El punto de la matriz hace contribución cero, por lo que tenemos una ecuación que da el valor del coeficiente en el punto debajo del punto azul como un múltiplo del valor en el punto azul. Entonces podemos continuar bajando al siguiente punto. En cambio, podríamos haber subido desde el punto azul usando triángulos rojos incompletos; de hecho, podemos continuar alrededor del borde de toda la matriz. Entonces, una vez que se fijan los valores a lo largo de los bordes, los triángulos de recursión se pueden utilizar para moverse hacia adentro y encontrar el resto.

El punto de esta sección es establecer que, aparte de una constante multiplicativa global que debe fijarse mediante normalización, todos los coeficientes CG para este valor de se\(j\) pueden encontrar únicamente a partir de las relaciones de recursión. La razón por la que esto es importante es porque la misma estructura algebraica, y por lo tanto las mismas relaciones de recursión, se utilizan para definir tensores esféricos, por lo que también se pueden combinar usando los mismos coeficientes CG. (Todavía necesitamos una convención de signos aquí para presentar una tabla completa: hasta el momento, los diferentes valores de total\(j\) tienen fases relativas arbitrarias).