10.1: Teoría de la dispersión

Casi todo lo que sabemos sobre núcleos y partículas elementales ha sido descubierto en experimentos de dispersión, desde la sorpresa de Rutherford al descubrir que los átomos tienen su masa y carga positiva concentrada en núcleos casi puntuales, hasta los descubrimientos más recientes, en una escala de longitud mucho menor, que los protones y los neutrones en sí mismos están constituidos por quarks aparentemente puntiformes.

El modelo más simple de un experimento de dispersión se da resolviendo la ecuación de Schrödinger para una onda plana que incide en un potencial localizado. Un potencial\(V(r)\) podría representar lo que un electrón rápido encuentra al golpear un átomo, o una partícula alfa un núcleo. Obviamente, representar cualquier sistema de este tipo por un potencial es solo un comienzo, pero en ciertos rangos de energía es bastante razonable, ¡y tenemos que empezar por alguna parte!

El escenario básico es disparar en una corriente de partículas, todas con la misma energía, y detectar cuántas son desviadas en una batería de detectores que miden ángulos de desviación. Suponemos que todas las partículas entrantes están representadas por paquetes de ondas de la misma forma y tamaño, por lo que debemos resolver la ecuación dependiente del tiempo de Schrödinger para dicho paquete de ondas y encontrar las amplitudes de probabilidad para las ondas salientes en diferentes direcciones en algún momento posterior después de que se haya producido la dispersión. Pero adoptamos un enfoque más simple: asumimos que el conjunto de ondas tiene una energía bien definida (y por lo tanto un impulso), por lo que tiene muchas longitudes de onda largas. Esto significa que durante el proceso de dispersión se parece mucho a una onda plana, y durante un período de tiempo la dispersión es independiente del tiempo. Asumimos, entonces, que el problema se aproxima bien resolviendo la ecuación de Schrödinger independiente del tiempo con una onda plana entrante. ¡Esto es mucho más fácil!

Todo lo que podemos detectar son ondas salientes muy fuera de la región de dispersión. Para una onda plana entrante\(e^{i\vec{k}\cdot\vec{r}}\), la función de onda lejos de la región de dispersión debe tener la forma\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+f(\theta,\varphi)\frac{e^{i k r}}{r} \label{10.1.1}\]

donde\(\theta,\varphi\) se miden con respecto a la dirección entrante.

Tenga en cuenta que la amplitud de dispersión\(f(\theta,\varphi)\) tiene las dimensiones de longitud.

No nos preocupamos por la normalización general, porque lo relevante es la fracción del haz entrante dispersado en una dirección particular, o, para ser más precisos, en un pequeño ángulo sólido\(d\Omega\) en la dirección\(\theta,\varphi\). La corriente entrante de partículas (con la normalización anterior) es\(\hbar k/m=v\) a través de la unidad de área perpendicular al haz entrante, la corriente de salida en el ángulo pequeño\(d\Omega\) es\((\hbar k/m)|f(\theta,\varphi)|^2d\Omega\). Es evidente que esta corriente saliente corresponde a la corriente entrante original que fluye a través de un área perpendicular de tamaño\(d\sigma(\theta,\varphi)=|f(\theta,\varphi)|^2d\Omega\), y\[ \frac{d\sigma}{d\Omega}=|f(\theta,\varphi)|^2 \label{10.1.2}\]

se llama la sección transversal diferencial para la dispersión en la dirección\( \theta,\varphi\).

La descripción independiente del tiempo

Revisaremos la formulación independiente del tiempo de la teoría de la dispersión, primero como se presenta en Baym, en términos de la ecuación estándar de Schrödinger wavefuntions, luego hacer lo mismo a la Sakurai, en el lenguaje más formal, pero por supuesto equivalente, de bras y kets. El enfoque de la función de onda Schrödinger es una introducción más fácil, pero el lenguaje formal es más conveniente para analizar la estructura de términos de orden superior.

En realidad, el tratamiento de Baym no es del todo independiente del tiempo, en el sentido de que usa un conjunto de ondas entrante, pero es uno de gran longitud, bien aproximado por una onda plana. Sakurai va directo a la ola de avión, y nosotros también. Este caso recuerda mucho a la dispersión unidimensional, en la que una onda plana desde la izquierda genera ondas salientes en ambas direcciones, y las amplitudes pueden calcularse a partir de la ecuación de Schrödinger para un único estado propio de energía. La única diferencia es que en 3D habrá ondas salientes en todas las direcciones.

Siguiendo a Baym, la ecuación de Schrödinger es:

\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)\psi_{\vec{k}}(\vec{r})=V(\vec{r})\psi_{\vec{k}}(\vec{r}),\;\; where\;\; E_k=\frac{\hbar^2k^2}{2m}. \label{10.1.3}\]

Esto\(\psi_{\vec{k}}\) lo tomamos para tener un componente de onda plana entrante\(e^{i\vec{k}\cdot\vec{r}}\). La normalización general es irrelevante, ya que la sección transversal diferencial depende únicamente de la relación entre la amplitud de la onda dispersada y la de la onda entrante.

El enfoque estándar de una ecuación como la anterior es transformarla en una ecuación integral usando las funciones de Green. Si\(V(\vec{r})\) es pequeño (lo pequeño que tiene que ser se aclarará más adelante) la ecuación integral puede entonces resolverse por iteración.

La función de Green\(G(\vec{r},\vec{k})\) es esencialmente la inversa del operador diferencial,\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)G(\vec{r},\vec{k})=\delta(\vec{r}). \label{10.1.4}\]

Esta no es una definición matemáticamente única: claramente, podemos agregar a\(G(\vec{r},\vec{k})\) cualquier solución de la ecuación homogénea\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)\varphi (\vec{r},\vec{k})=0, \label{10.1.5}\]

por ejemplo, la onda del avión entrante.

Si escribimos la ecuación integral

\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+\int d^3r' G(\vec{r}-\vec{r}' )V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ) \label{10.1.6}\]

esta\(\psi_{\vec{k}}(\vec{r})\) es sin duda una solución a la ecuación original de Schrödinger, ya que se verifica fácilmente aplicando el operador\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right) \label{10.1.7}\]

a ambos lados de la ecuación.

La ecuación integral puede resolverse formalmente por iteración, y para “pequeños”\(V\) la solución convergerá. Pero esto realmente no va a funcionar, recuerda, ¡no tenemos una única\(G(\vec{r},\vec{k})\)! Tenemos que solucionarlo\(G(\vec{r},\vec{k})\) conectándonos mejor con el problema de dispersión que estamos tratando de resolver.

Sabemos que nuestra solución tiene una sola onda plana entrante, y ondas salientes en todas las demás direcciones, generadas por la interacción de la onda plana con el potencial. Pero la ecuación de Schrödinger podría describir igualmente las ondas entrantes en las otras direcciones. Al definir la función del Verde y escribir la ecuación integral, en ninguna parte hemos especificado la forma distante de la función de onda, es decir, no hemos requerido que la función del Verde en el lado derecho de la ecuación integral solo genere ondas salientes. Para ver cómo hacer esto, debemos escribir la función del Verde misma como una suma sobre las ondas, es decir, una transformada de Fourier, y ver cómo eliminar las ondas entrantes no físicas (para el problema actual) en esa suma.

La forma explícita de la función del Verde es\[ G(r,k)=\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k}' \cdot\vec{r}}}{E_k-\frac{\hbar^2k'^2}{2m}}=-\frac{m}{2\pi^2ir\hbar^2}\int_{-\infty}^{\infty}\frac{k' dk' e^{ik'r}}{k'^2-k^2}. \label{10.1.8}\]

Tenga en cuenta que\(G(r,k)\) solo depende de\(\vec{k}\) a través\(E_k\), y solo de\(\vec{r}\) a través\(r\), ya que la integración \(\vec{k}'\)es sobre todas las direcciones. Es fácil verificar que esta función de Green satisface la ecuación diferencial, aplicando el operador diferencial a la primera integral anterior: el resultado es cancelar el denominador en la integral, dejando justo\(\int \frac{d^3k'}{(2\pi)^3}e^{i\vec{k}' \cdot\vec{r}}\), que es la función\(\delta\) - en\(\vec{r}\).

Para obtener la segunda forma de\(G(r,k)\) en la ecuación anterior, primero hacemos la integración angular\(d(\cos\theta)\) para obtener\((e^{ik'r}-e^{-ik'r})/ik' r\), luego reorganizamos la integral sobre el\(-e^{-ik'r}\) término cambiando el signo de\(k' \), por lo que se convierte en una integral de\(-\infty\) a 0 en lugar de 0 a\(\infty\). Después sumamos los dos términos (el\(e^{ik'r}\) y el\(-e^{-ik'r}\)) juntos para dar una integral de\(-\infty\) a\(\infty\). Esta integral de\(-\infty\) a\(\infty\) se realiza luego mediante la integración de contorno, al menos, después de haber descubierto qué hacer con las singularidades en\(k' =\pm k\).

Para que se defina la integral, el contorno debe distorsionarse ligeramente para que desvíe estos polos.

Es en este punto nos alimentamos en nuestro conocimiento físico de la situación: que en el proceso de dispersión, el segundo término en\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+\int d^3r' G(\vec{r}-\vec{r}' )V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ), \label{10.1.9}\]

es decir, el término de función del Verde, tiene que ser una suma sobre las ondas salientes solamente. Y, podemos garantizar esto distorsionando el contorno de integración en la dirección correcta, de la siguiente manera.

La integral del contorno tiene que ser evaluada cerrando el contorno. Ya que\(r\) es positivo\(e^{ik'r}\) va a cero en el medio\(k'\) plano superior, pero diverge en la mitad inferior, por lo que debemos cerrar el contorno en el plano de la mitad superior para asegurar que no haya contribución desde el semicírculo al infinito. Por lo tanto, para obtener las ondas salientes deseadas,\(e^{ikr}\) pero no\(e^{-ikr}\), nuestro contorno cerrado en el medio plano superior debe rodear el polo en\(k' =+k\) pero no el uno en\(k' =-k\). (\(e^{ikr}\)sí representa ondas salientes: la dependencia del tiempo suprimida es\(e^{-iEt/\hbar} =e^{-i\omega t}\), dando\(e^{i(kr-\omega t)}\).) En otras palabras, la configuración relativa de la parte del eje real del contorno y los dos polos tiene que ser:

x (polo)

____________________________________________________________________________________________________________________________________________________________

x (polo en\(k' =-k-i\varepsilon\)) (polo en\(k' =+k+i\varepsilon\))

En lugar de mover el contorno ligeramente fuera del eje real para evitar los polos, hemos movido ligeramente los polos en su lugar. Estos movimientos son infinitesimales, por lo que el que se mueve no hace diferencia en el valor de la integral. Es más conveniente mover los polos, como se muestra, porque este movimiento se puede incluir eficientemente en la integral simplemente agregando una parte imaginaria infinitesimal al denominador:\[ G_+(r,k)=\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k}' \cdot\vec{r}}}{E_k-\frac{\hbar^2k'^2}{2m}+i\varepsilon}=-\frac{m}{2\pi^2ir\hbar^2}\int_{-\infty}^{\infty}\frac{k' dk' e^{ik'r}}{k'^2-k2-i\varepsilon}. \label{10.1.10}\]

Observe que hemos escrito\(G_+\) en lugar de\(G\), porque\(G\) puede denotar cualquier solución de\[ \left(\frac{\hbar^2}{2m}\nabla^2+E_k\right)G(\vec{r},\vec{k})=\delta(\vec{r}) \label{10.1.11}\]

y estamos especificando la solución particular teniendo sólo ondas salientes. En contraste con\(G\),\(G_+\) está bien definido y único. (Hay otra solución perfectamente válida que tiene solo ondas entrantes, pero es irrelevante para el problema de la dispersión. La diferencia entre las soluciones entrante y saliente satisface la ecuación homogénea que tiene cero en el lado derecho).

Una vez que movemos los polos ligeramente como se describió anteriormente, el polo at\(k' =+k+i\varepsilon\) es de hecho la única singularidad del integrando que se encuentra dentro del contorno de integración (cerrado en el medio plano superior), por lo que el valor de la integral es solo la contribución de este polo, es decir,\[ G_+(r,k)=-\frac{m}{2\pi^2ir\hbar^2}(2\pi i)\frac{ke^{ikr}}{2k}=-\frac{m}{2\pi\hbar^2}\frac{e^{ikr}}{r} \label{10.1.12}\]

.

Por lo tanto, la\(i\varepsilon\) prescripción (como a veces se le llama) en\(G_+\) sí nos da lo que queremos: una solución que tenga solo ondas salientes, y la ecuación integral se convierte en:\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{e^{ik |  \vec{r}-\vec{r}' |}}{|\vec{r}-\vec{r}' |}V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.13}\]

Esto se puede escribir de manera más sencilla si asumimos el potencial de ser localizados, para que podamos tomar\(|\vec{r}|\gg |\vec{r}' |\). En este caso, es una buena aproximación para tomar\(|\vec{r}-\vec{r}' |=r\) en el denominador. No obstante, esta aproximación no se puede hacer en el exponencial, porque al orden inicial (ver diagrama) y aunque el segundo término es mucho menor que el primero, es una fase, que puede ser de unidad de orden. Dicho factor, por supuesto, debe incluirse para que las contribuciones a la integral de diferentes regiones del potencial se sumen con las fases relativas correctas.

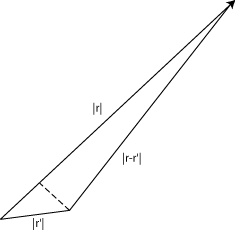
\[ k|\vec{r}-\vec{r}' |=kr-k\hat{\vec{r}}\cdot\vec{r}' =kr-\vec{k}_f\cdot\vec{r}' \label{10.1.14}\]

Por lo tanto, suponiendo que la distancia del detector\(r\) es mucho mayor que el rango del potencial, podemos escribir\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\frac{e^{i kr}}{r}\int d^3r' e^{-i \vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.15}\]

La aproximación del Born

De la ecuación anterior, la aproximación de primer orden a la dispersión se da reemplazando\(\psi\) en la integral de la derecha por el término de orden cero\(e^{i\vec{k}\cdot\vec{r}}\),\[ \psi_{\vec{k}(Born)}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\frac{e^{i kr}}{r}\int d^3r' e^{i\vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) . \label{10.1.16}\]

Esta es la aproximación Born. En cuanto a la amplitud de dispersión\(f(\theta,\varphi)\), que definimos en términos de la función de onda asintótica:

\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}+f(\theta,\varphi)\frac{e^{ikr}}{r} \label{10.1.17}\]

la aproximación Born es:

\[ f_{Born}(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r' e^{i \vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' ) =-\frac{m}{2\pi\hbar^2}\int d^3r' e^{-i \vec{q}\cdot\vec{r}'} V(\vec{r}' ) \label{10.1.18}\]

donde\(\hbar \vec{q}\) esta la transferencia de momentum,\(\hbar \vec{q}=\hbar (\vec{k}_f-\vec{k})\). (Dado que los momentos entrante y saliente tienen igual magnitud, es fácil verificarlo)\(q=2k\sin\theta/2\).

La física esencial aquí es que una partícula dispersa con el cambio de momento\(\hbar \vec{q}\) es dispersada por el componente\(\vec{q}\) -Fourier del potencial; uno puede imaginar el potencial como una acumulación de componentes de Fourier, cada uno de los cuales actúa como una rejilla de difracción. Las correcciones de orden superior a la aproximación Born corresponden a dispersiones sucesivas de estas rejillas; estos órdenes superiores se generan por iteración de\[ \psi_{\vec{k}}(\vec{r})=e^{i\vec{k}\cdot\vec{r}}-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{e^{ik |  \vec{r}-\vec{r}' |}}{|\vec{r}-\vec{r}'|}V(\vec{r}' ) \psi_{\vec{k}}(\vec{r}' ). \label{10.1.19}\]

Es importante establecer cuándo la aproximación Born es buena: a veces no lo es, en realidad, solo estamos haciendo la teoría de la perturbación disfrazada, entonces necesitamos que la perturbación sea pequeña, es decir, reemplazar\(\psi_{\vec{k}}(\vec{r}' )\) por\(e^{i\vec{k}\cdot\vec{r}'}\) en la integral a la derecha en la ecuación anterior solo debería hacer una pequeña diferencia al valor de\(\psi_{\vec{k}}(\vec{r})\) dado haciendo la integral. Este es, por supuesto, un ejercicio bastante complicado de autoconsistencia.

Intentemos estimar qué diferencia hace la sustitución de\(\psi_{\vec{k}}(\vec{r}' )\) por\(e^{i\vec{k}\cdot\vec{r}'}\) en el integrando para el caso común de un potencial esféricamente simétrico\(V(r)\) parametrizado por profundidad\(V_0\) y rango\(r_0\). La integral se encuentra efectivamente solo sobre una región de tamaño\(r_0\) alrededor del origen.

Primero consideremos la dispersión de baja energía,\(kr_0<1\) digamos, por lo que para fines de estimación podemos reemplazar el término exponencial por 1 en la región de integración. También asumimos que donde\(\psi\) aparece en la integral en el lado derecho de la ecuación también\(|\psi_{\vec{k}}(\vec{r}' )|\) está bastante cerca de 1 (recuerda que la integral está solo sobre un volumen dentro\(r_0\) o así del origen) y así solo la reemplazamos por 1. En otras palabras, estamos asumiendo que la onda plana entrante, la\(e^{i\vec{k}\cdot\vec{r}'}\), no se distorsiona dramáticamente dentro de ese volumen donde el potencial es significativo.

Ahora, hemos asumido que la función de onda cerca del origen está cerca de 1, así que poner ese valor en el integrando a la derecha sería mejor dar un valor para\(\psi_{\vec{k}}(\vec{r})\) en el lado izquierdo de la ecuación que está bastante cerca de 1. Las aproximaciones dan:\[ \psi_k(0)\approx 1-\frac{m}{2\pi\hbar^2}\int d^3r' \frac{V(r' )}{r'} ,\label{10.1.20}\]

por lo que la aproximación Born será razonable a bajas energías (\(kr_0<1\)) si el segundo término en el lado derecho es mucho menor que la unidad.

¿Cuándo es esto cierto para un potencial real? Tomando\(V(r)\) para tener profundidad\(V_0\) y rango\(r_0\), la aproximación Born es buena si:\[ \frac{m}{2\pi\hbar^2}\int_0^{r_0}4\pi r^2\frac{V_0}{r}dr\ll 1,\;\; or\;\; V_0\ll \frac{\hbar^2}{mr^2_0}. \label{10.1.21}\]

Observe que el lado derecho de esta desigualdad es de orden la energía cinética de una partícula confinada a un volumen igual al rango del potencial, por lo que la aproximación Born es válida a bajas energías siempre que el potencial esté muy por debajo de la fuerza necesaria para un estado ligado.

De hecho, la aproximación Born funciona mejor a energías superiores, porque el término de fase oscilante en\(-\frac{m}{2\pi\hbar^2}\int d^3r' e^{-i \vec{q}\cdot\vec{r}'} V(\vec{r}' )\) reduce el valor de la integral por un factor de orden de magnitud\(1/(kr_0)\). Esto significa que la condición se vuelve\(V_0\ll kr_0\frac{\hbar^2}{mr^2_0}\), siempre satisfecha con energías suficientemente altas.

La ecuación de Lippmann-Schwinger

Resulta esclarecedor, especialmente en la comprensión de la dispersión más allá de la aproximación Born, refundir la derivación de la función de Green de la amplitud de dispersión en el lenguaje más formal de los sostenes, kets y operadores. La función de Green se introdujo en la sección anterior como la inversa (no única) del operador\[ E_k-H_0=\left(\frac{\hbar^2}{2m}\nabla^2+E_k\right) .\label{10.1.22}\]

(Observación entre paréntesis: en el cálculo numérico, la función de onda podría especificarse en puntos de una celosía en el espacio, y un operador diferencial como este se representaría como un operador de diferencia, es decir, como una matriz grande pero finita que opera sobre un vector grande cuyos elementos eran los valores de ondulación en puntos de la celosía. La función de Green sería entonces la matriz inversa con condiciones de límite apropiadas especificadas para asegurar la singularidad.)

Puramente formalmente (y siguiendo a Sakurai), escribiendo\(H=H_0+V\), con\(H_0\) el operador de energía cinética\(\vec{p}^2/2m\), el estado de onda plana entrante es una solución de\[ H_0|\vec{k}\rangle  =E_k|\vec{k}\rangle . \label{10.1.23}\]

Queremos resolver\[ (H_0+V)|\psi\rangle  =E_k|\psi\rangle . \label{10.1.24}\]

La transformación de una ecuación diferencial a una ecuación integral en este lenguaje es:\[ |\psi\rangle  = |\vec{k}\rangle +\frac{1}{E_k-H_0}V|\psi\rangle . \label{10.1.25}\]

Esto da la onda entrante no perturbada para\(V=0\), y al operar en ambos lados de la ecuación con\(E-H_0\), encontramos que realmente\(|\psi\rangle\) satisface la ecuación completa de Schrödinger. Pero por supuesto esta transformación de una ecuación diferencial a una integral tiene el mismo defecto que el tratamiento anterior:\(H_0\) tiene un continuo de valores propios en el límite de volumen infinito, por lo que la ecuación del operador se vuelve mal definida para aquellos autoestados con energía arbitrariamente cercana a la energía entrante , y esos son precisamente los estados de relevancia física.

Para hacer explícito que éste es efectivamente el problema que ya resolvimos, traduzcamos al idioma anterior. Primero toma el producto interior con el sujetador\(\langle \vec{r}|\):\[ \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\langle \vec{r}|\frac{1}{E_k-H_0}V|\psi\rangle . \label{10.1.26}\]

A continuación, inserte una representación de la unidad como una suma sobre los propios estados de impulso (y por lo tanto de\(H_0\)) en el último término:

\[ \begin{matrix} \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \langle \vec{k}' |\frac{1}{E_k-H_0}V|\psi\rangle \\ = \langle \vec{r}|\vec{k}\rangle +\int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \frac{1}{E_k-E_k'} \langle \vec{k}' |V|\psi\rangle . \end{matrix} \label{10.1.27}\]

Por último, insertar otra representación de unidad como suma sobre los propios estados de posición en el último término:\[ \langle \vec{r}|\psi\rangle  = \langle \vec{r}|\vec{k}\rangle +\int d^3r' \int \frac{dk' }{(2\pi)^3}\langle \vec{r}|\vec{k}' \rangle \frac{1}{E_k-E_k'}\langle \vec{k}' |\vec{r}' \rangle \langle \vec{r}' |V|\psi\rangle . \label{10.1.28}\]

Comparando esta expresión con la ecuación integral en la discusión anterior, es evidente que efectivamente son equivalentes, y por lo tanto la prescripción correcta de i\ varepsilon para dar la función de onda dispersa,\[ |\psi\rangle  =  |\vec{k}\rangle +\frac{1}{E_k-H_0+i\varepsilon}V|\psi\rangle  =  |\vec{k}\rangle+G_+ V|\psi\rangle \label{10.1.29}\]

donde\[ G_+=\frac{1}{E_k-H_0+i\varepsilon}=\int \frac{d^3k'}{(2\pi)^3}\frac{|\vec{k}' \rangle \langle \vec{k}' |}{E_k-E_k' +i\varepsilon} \label{1.1.30}\]

en cuya forma es evidente que\(\langle \vec{r}|G_+|\vec{r}' \rangle\) es lo mismo que\(G_+(\vec{r}-\vec{r}' )\) en el trabajo anterior.

Esta ecuación para la onda dispersa\(|\psi\rangle\) se denomina ecuación de Lippmann-Schwinger.

Nota: Sakurai define la función de su Green como

\[ G_+(Sakurai)=\frac{\hbar^2}{2m}\frac{1}{E-H_0+i\varepsilon}\cdot\label{10.1.31}\]

Ahora que tenemos un operador de función de Green bien definido\(G_+\), la ecuación de Lippmann-Schwinger se puede resolver formalmente:\[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\psi\rangle , \;\; so \;\; |\psi\rangle  = \frac{1}{1-G_+ V}|\vec{k}\rangle , \label{10.1.32}\]

con una solución en serie\[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\vec{k}\rangle +G_+ VG_+ V|\vec{k}\rangle +G_+ VG_+ VG_+ V|\vec{k}\rangle +\dots \label{10.1.33}\]

solo una versión formal de la solución que encontramos anteriormente.

La Matriz de Transición

Operando en ambos lados de la ecuación anterior con\(V\),\[ V|\psi\rangle  =  V|\vec{k}\rangle +VG_+ V|\vec{k}\rangle +VG_+ VG_+ V|\vec{k}\rangle +\dots=T|\vec{k}\rangle \label{10.1.34}\]

definir la “matriz de transición”\(T\) mediante\[ T=V+VG_+V+VG_+VG_+V+\dots=V+V\frac{1}{E-H_0+i\varepsilon}V+\dots \label{10.1.35}\]

En términos de este operador de matriz de transición, se puede escribir la onda dispersa\[ |\psi\rangle = |\vec{k}\rangle  +G_+ T|\vec{k}\rangle . \label{10.1.36}\]

Comparando esto con\[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\psi\rangle , \label{10.1.37}\]

y recordando que la aproximación Born viene dada por\[ |\psi\rangle_{Born}= |\vec{k}\rangle +G_+ V|\vec{k}\rangle , \label{10.1.38}\]

vemos que\(T\) es una especie de potencial generalizado, incluyendo todos los términos de orden superior, de manera que así como la aproximación Born dio la amplitud de dispersión en términos de\(V\),\[ f^{Born}(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r' e^{i \vec{k}\cdot\vec{r}' -\vec{k}_f\cdot\vec{r}'} V(\vec{r}' )  \label{10.1.39}\]

el resultado exacto incluyendo todos los términos de orden superior debe tener la misma estructura con el\(T\) reemplazo\(V\). Por supuesto, a diferencia\(V(\vec{r})\), no\(T\) es una matriz diagonal en\(r\) - espacio: depende de dos variables espaciales, y su transformada de Fourier es por lo tanto una función de dos momentos, es decir, el entrante\(\vec{k}\) y el disperso\(\vec{k}'\). Así encontramos:\[ f(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int d^3r\int d^3r' e^{i \vec{k}\cdot\vec{r}-\vec{k}' \cdot\vec{r}'} T(\vec{r}' ,\vec{r})=-\frac{m}{2\pi\hbar^2}\langle \vec{k}' |T|\vec{k}\rangle . \label{10.1.40}\]

Hemos sustituido la expresión\(\vec{k}_f\) en el Born por\(\vec{k}'\). Sakurai tiene un extra\((2\pi)^3\) en el término a la derecha, porque usa\(\langle \vec{k}|\vec{k}' \rangle =\delta(\vec{k}-\vec{k'})\),\(\langle \vec{r}|\vec{k}\rangle =\frac{e^{i\vec{k}\cdot\vec{r}}}{(2\pi)^{3/2}}\), nosotros usamos\(\langle \vec{k}|\vec{k}' \rangle =(2\pi)^3\delta(\vec{k}-\vec{k'})\),\(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\).

El Teorema Óptico

El Teorema Óptico relaciona la parte imaginaria de la amplitud de dispersión hacia adelante con la sección transversal total,\[ Im\, f(\theta=0)=\frac{k\sigma_{tot}}{4\pi}. \label{10.1.41}\]

El contenido físico de este teorema inicialmente misterioso se volverá mucho más claro después de que discutamos las ondas parciales y algunos efectos geométricos. Nos dice que\(f\) no puede ser real en todas las direcciones, y que en particular\(f\) tiene una parte imaginaria positiva en la dirección hacia adelante. Aquí hemos incluido la prueba para que conste, pero puedes saltarla por ahora. Pero tenga en cuenta que esta prueba es más general que la simple dada (posteriormente) en la sección sobre ondas parciales, en que aquí no asumimos el potencial de tener simetría esférica.

De la expresión para\(f(\theta,\varphi)\) arriba, vemos que debemos encontrar la parte imaginaria de\(\langle \vec{k}|T|\vec{k}\rangle\).

Recordemos que\[ V|\psi\rangle =  T|\vec{k}\rangle , \label{10.1.42}\]

por lo que tenemos que encontrar\[ Im\,\langle \vec{k}|V|\psi\rangle =Im\left[\left(\langle \psi|-\langle \psi|V\frac{1}{E-H_0-i\varepsilon}\right) V|\psi\rangle \right]. \label{10.1.43}\]

Dado que\(V\) es hermitiano, la única parte imaginaria del elemento matriz anterior proviene del\(i\varepsilon\), recordando que\[ \frac{1}{E-H_0-i\varepsilon}=\frac{P}{E-H_0}+i\pi\delta(E-H_0). \label{10.1.44}\]

Por lo tanto,\[ Im\,\langle \vec{k}|V|\psi\rangle =-\pi\langle \psi|V\delta(E-H_0)V|\psi\rangle . \label{10.1.45}\]

Nuevamente usando\[ V|\psi\rangle =  T|\vec{k}\rangle \label{10.1.42}\]

podemos reescribir la ecuación\[ Im\,\langle \vec{k}|T|\vec{k}\rangle =Im\,\langle \vec{k}|V|\psi\rangle =-\pi\langle \psi|V\delta(E-H_0)V|\psi\rangle =-\pi\langle \vec{k}|T^{\dagger}\delta(E-H_0)T|\vec{k}\rangle . \label{10.1.46}\]

Insertar un conjunto completo de estados de onda plana en el elemento final de la matriz anterior da\[ \begin{matrix} Im\,\langle \vec{k}|T|\vec{k}\rangle =-\pi\langle \vec{k}|T^{\dagger}\delta(E-H_0)T|\vec{k}\rangle \\ =-\pi\int \frac{d^3k'}{(2\pi)^3}\langle \vec{k}|T^{\dagger}|\vec{k}' \rangle \langle \vec{k}' |T|\vec{k}\rangle \delta(E-\frac{\hbar^2k'^2}{2m}) \\ =-\pi\int \frac{d\Omega' }{(2\pi)^3}\frac{mk}{\hbar^2}|\langle \vec{k}' |T|\vec{k}\rangle |^2. \end{matrix} \label{10.1.47}\]

(Esta es la misma fórmula que la de Sakurai en 7.3: nuestro extra\((2\pi)^3\) en el denominador sólo es aparente, porque nuestros estados de onda plana difieren de los suyos por un factor\((2\pi)^{3/2}\).)

Formulación dependiente del tiempo de la teoría de dispersión

En la formulación independiente del tiempo presentada anteriormente, resolvimos la ecuación de Lippmann-Schwinger para encontrar\[ |\psi\rangle  =  |\vec{k}\rangle +G_+ V|\vec{k}\rangle +G_+ VG_+ V|\vec{k}\rangle +G_+ VG_+ VG_+ V|\vec{k}\rangle +\dots \label{10.1.48}\]

donde\[ G_+(E)=\frac{1}{E-H_0+i\varepsilon}=\int \frac{d^3k'}{(2\pi)^3}\frac{|\vec{k'}\rangle\langle\vec{k'}|}{E-E_{k'} +i\varepsilon} \label{10.1.49}\]

y\(E=E_k\).

(Recordatorio sobre nuestra convención de normalización de función de onda: siempre tenemos un denominador\(2\pi\) para una integral\(dk\). Esto significa que el operador de identidad como una suma sobre operadores de proyección de onda plana es\(I=\int \frac{d^3k}{(2\pi)^3}|\vec{k}\rangle \langle \vec{k}| \). La normalización es\(\langle \vec{k}|\vec{k}' \rangle =(2\pi)^3\delta(\vec{k}-\vec{k'})\), y\(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\). Sakurai usa\(\langle \vec{k}|\vec{k}' \rangle =\delta(\vec{k}-\vec{k'})\),\(\langle \vec{r}|\vec{k}\rangle =\frac{e^{i\vec{k}\cdot\vec{r}}}{(2\pi)^{3/2}}\) y al\(I=\int d^3k|\vec{k}\rangle \langle \vec{k}|\) igual que Shankar en el Capítulo 1, para una dimensión, página 67, pero más tarde, Capítulo 21 página 585, Shankar ha cambiado a nuestra notación, ¡así que ten cuidado! Nuestra convención también es utilizada por Baym y por Peskin.)

De hecho, esta función\(G_+\) es la transformada de Fourier del propagador que discutimos el semestre pasado. Para ver cómo se produce esto, tome el elemento matriz entre dos estados propios de posición y la transformada de Fourier de la energía al tiempo:\[ \begin{matrix} G_+(\vec{r},\vec{r'},t)=\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\langle \vec{r}|G_+|\vec{r'}\rangle \\ =\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\int \frac{d^3k'}{(2\pi)^3}\frac{\langle \vec{r}|k' \rangle \langle k' |\vec{r}' \rangle}{E-E_{k'} +i\varepsilon} \\ =\frac{1}{2\pi}\int e^{-iEt/\hbar} dE\int \frac{d^3k'}{(2\pi)^3}\frac{e^{i\vec{k'}\cdot(\vec{r}-\vec{r'})}}{E-E_{k'} +i\varepsilon}. \end{matrix} \label{10.1.50}\]

La integral sobre\(E\) está a lo largo del eje real, y el contorno se cierra en el medio plano donde el integrando va a cero para en la dirección imaginaria, es decir, en el medio plano inferior para\(t>0\) y el medio plano superior para\(t<0\). Pero con el\(i\varepsilon\) término mostrado, todas las singularidades del integrando están en el plano de la mitad inferior. De ahí\(G_+\) que sea idéntico cero para\(t<0\).

Porque\(t>0\),\(G_+\) es solo el propagador de partículas libres entre los dos puntos (aparte del factor de fase\(-i\)):\[ G_+(\vec{r},\vec{r'},t)=-i\int \frac{d^3k'}{(2\pi)^3}e^{i\vec{k'}\cdot(\vec{r}-\vec{r'})-iE_{k'}t/\hbar} . \label{10.1.51}\]

Para resumir: los términos en la solución en serie de la ecuación de Lippmann-Schwinger pueden interpretarse como dispersiones sucesivas de los componentes de Fourier de un potencial, con propagación de onda plana en el medio, con el signo del\(i\varepsilon\) término asegurando que solo hay ondas salientes de cada dispersión. En la versión transformada de Fourier anterior, la suma es sobre dispersión en todos los puntos posibles donde el potencial es distinto de cero, con\(G_+\) propagación en el medio,\(i\varepsilon\) asegurando que la trayectoria de dispersión solo avance en el tiempo.

El semestre pasado, definimos el propagador de partículas libres como el operador\(U(t)=e^{-iH_0t/\hbar}\). El propagador describe el desarrollo de la función de onda de partículas libres en el tiempo, así que naturalmente\(U(t)=0\) para\(t<0\). Luego Fourier transformando el propagador de\(t\) a\(E\), e insertando un factor infinitesimal que decae exponencialmente para definir la integral en el infinito, encontramos\[ U(E)=\int_{0}^{\infty} e^{iEt/\hbar} e^{-iH_0t/\hbar}e^{-\varepsilon t/\hbar} dt=\frac{i\hbar}{E-H_0+i\varepsilon}. \label{10.1.52}\]

Tenga en cuenta que los propagadores\(U\) y\(G_+\) difieren por un factor de\(i\hbar\), específicamente\[ G_+(t)=\frac{-i}{\hbar} \theta(t)e^{-iH_0t/\hbar}. \label{10.1.53}\]

Seguimos la notación de Sakurai (sección 7.11), esta es la función de Green correctamente normalizada para la ecuación de Schrödinger de partículas libres dependiente del tiempo: es la solución de\[ \left( i\hbar \frac{\partial}{\partial t}-H_0\right) G_+(t)=\delta(t) \label{10.1.54}\]

que propaga hacia adelante en el tiempo. La razón por la que los propagadores\(U\) y\(G_+\) difieren por un factor de\(i\hbar\) es que la ecuación de Lippmann-Schwinger se puede generar como una secuencia de tiempo utilizando la representación de interacción de la teoría de perturbación de orden superior descrita anteriormente en el curso, esencialmente expandiéndose\(e^{-i(H_0+V)t/\hbar}\) como un tiempo- expansión de serie ordenada en\(V\), y cada factor\(V\) tiene un acompañamiento\(1/(i\hbar )\), estos factores se cuidan mediante el uso\(G_+\) en lugar de\(U\).

Ejercicio: en esa conferencia anterior, dimos el término de segundo orden como:\[ c^{(2)}_n(t)=\left(\frac{1}{i\hbar}\right)^2\sum_n\int_0^t\int_0^{t'} dt' dt' ' e^{-i\omega_f(t-t' )}\langle f|V_S(t' )|n\rangle e^{-i\omega_n(t' -t' ' )}\langle n|V_S(t' ' )|i\rangle e^{-i\omega it' '} \label{10.1.55}\]

Supongamos que el potencial\(V\) es constante en el tiempo. Fourier transforma esta expresión de\(t\) a\(E\)\(E=\hbar \omega\),, y establecer que tiene la estructura\(G_+(E)VG_+(E)VG_+(E)\).

La sección transversal nacida de la teoría dependiente del tiempo

Establecimos en la conferencia sobre Teoría de la Perturbación Dependiente del Tiempo que al orden principal en la perturbación, la tasa de transición de un estado inicial\(i\) a un estado final\(f\) viene dada por la Regla de Oro de Fermi:\[ R_{i\to f}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i). \label{10.1.56}\]

Podemos usar este resultado para encontrar, en orden inicial, la tasa de dispersión de una onda plana entrante a cualquier estado de onda plana saliente que tenga la misma energía y, por lo tanto, al agregar la velocidad sobre las direcciones de onda plana que apuntan dentro de un ángulo sólido pequeño dado\(d\Omega\), rederivar la aproximación Born.

Conceptualmente, sin embargo, esto es un poco complicado. De la solución anterior de la ecuación de Schrödinger, sabemos que la onda saliente es esférica, por lo que en una dirección particular la amplitud disminuye. ¡Pero eso no pasa con una ola de avión! La forma más clara de manejar esto es poner el sistema en una caja grande, un cubo de lado\(L\), con condiciones de contorno periódicas. Esto hace que sea más fácil contar estados y normalizar correctamente las ondas planas; por supuesto, en el límite de una caja grande, las ondas planas forman un conjunto completo, por lo que cualquier onda esférica puede expresarse como una suma sobre estas ondas planas.

En esta sección, entonces, utilizamos ondas planas normalizadas por caja:\[ |\vec{k}\rangle =\frac{1}{L^{3/2}}e^{i\vec{k}\cdot\vec{r}},\;\; \langle \vec{k'}|\vec{k}\rangle =\delta_{\vec{k}\vec{k'}} . \label{10.1.57}\]

Entonces\[ \langle f|V|i\rangle =\frac{1}{L^3}\int d^3re^{-i\vec{k}_f\cdot\vec{r}}V(\vec{r}) e^{i\vec{k}_i\cdot\vec{r}}=\frac{1}{L^3}\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r}) \label{10.1.58}\]

donde el impulso se transfiere a la partícula\(\hbar \vec{q}=\hbar (\vec{k}_f-\vec{k}_i)\).

Es importante señalar que estamos tomando la onda entrante para ser solo uno de los estados de onda plana normalizados satisfaciendo las condiciones de contorno periódico de la caja, por lo que ahora la corriente entrante, siendo de solo una de estas ondas planas, es\[ j_{in}=|\psi|^2v=\frac{1}{L^3}\frac{p}{m}. \label{10.1.59}\]

La Regla de Oro se convierte\[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i)d\Omega \label{10.1.60}\]

\(f\)denotando una onda plana que va hacia afuera dentro del ángulo sólido\(d\Omega\).

Ahora, la función\(\delta\) - simplemente cuenta el número de estados disponibles a la energía correcta (inicial), dentro del ángulo de dirección sólido final especificado. La densidad de estados en el espacio de momento (para el volumen\(L^3\) del espacio real) es un estado en cada volumen momento-espacio\((2\pi\hbar)^3/L^3\), por lo que usando\(dE/dp=p/m\), la densidad de estados en energía para el ángulo sólido saliente\(d\Omega\) es\(L^3mpd\Omega/(2\pi\hbar)^3\).

Poniendo todo esto junto\[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\frac{1}{L^3}\int d^3xe^{-i\vec{q}\cdot\vec{x}}V(\vec{x})|^2L^3mpd\Omega/(2\pi\hbar)^3. \label{10.1.61}\]

La tasa de transición, la tasa de dispersión en\(d\Omega\), es solo la corriente incidente multiplicada por la sección transversal de dispersión infinitesimal\(d\sigma(\theta,\varphi)\) (esa fue nuestra definición de\(d\sigma\)),

\[ j_{in}(\frac{d\sigma(\theta,\varphi)}{d\Omega})d\Omega=R_{i\to(f\; in\; d\Omega)} \label{10.1.62}\]

porque nuestra definición de\(R_{i\to(f\; in\; d\Omega)}\) incluye la onda entrante apropiadamente normalizada.

Así que finalmente\[ \frac{d\sigma(\theta,\varphi)}{d\Omega}=\frac{R_{i\to(f\; in\; d\Omega)}}{j_{in}d\Omega}=\frac{m}{p}\frac{2\pi}{\hbar} |\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2mp/(2\pi\hbar)^3=|\frac{m}{2\pi\hbar^2}\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2. \label{10.1.63}\]

Nota al pie de página: la versión continua.

\[ R_{i\to(f\; in\; d\Omega)}=\frac{2\pi}{\hbar} |\langle f|V|i\rangle |^2\delta(E_f-E_i)d\Omega. \label{10.1.60}\]

En la versión continuum,\(\langle \vec{r}|\vec{k}\rangle =e^{i\vec{k}\cdot\vec{r}}\), por lo que el término del elemento matriz es justo\(|\int d^3re^{-i\vec{q}\cdot\vec{r}}V(\vec{r})|^2\). La función de energía\(\delta\) solo es significativa dentro de una integral, en este caso sobre el pequeño volumen de estados de dispersión salientes en el ángulo sólido\(d\Omega\) y energía igual a la energía entrante. Pero este\(k'\) sobreespacio integral debe incluir el\(1/(2\pi)^3\) factor, según nuestra regla, dando un término de espacio de fase saliente\[ \int \frac{d^3k'}{(2\pi)^3}\delta(E_{k'}-E_k)=d\Omega\int \frac{k'^2dk' }{(2\pi)^3} \delta\left(\frac{\hbar^2k'^2}{2m}-\frac{\hbar^2k^2}{2m}\right)=d\Omega\frac{k^2}{(2\pi)^3}\frac{m}{\hbar^2k}=d\Omega\frac{mp}{(2\pi\hbar)^3}. \label{10.1.64}\]

Esto establece que nuestras convenciones de normalización continua dan el mismo resultado que el obtenido de la normalización de caja.

Dispersión de electrones a partir de átomos

Este mismo enfoque, utilizando la Regla de Oro para derivar la velocidad de dispersión de orden principal, es útil para analizar la dispersión de electrones rápidos por átomos. El problema con los electrones lentos es que la función de onda necesita ser antisimétrica con respecto a todos los electrones presentes. Asumimos que los electrones rápidos tienen poca superposición con las funciones de ondas de electrones atómicos en el espacio de impulso, por lo que no tenemos que preocuparnos por la simetría.

Con esta aproximación, siguiendo a Sakurai (página 431) el elemento de la matriz de amplitud de dispersión es\[ \int d^3re^{i\vec{q}\cdot\vec{r}}\langle n|\left( -\frac{Ze^2}{r}+\sum_i\frac{e^2}{|\vec{r}-\vec{r}_i|}\right) |0\rangle \label{10.1.65}\]

donde el término potencial\(V(\vec{x})\) es el del núcleo, más la repulsión de los otros electrones en las posiciones\(\vec{x}_i\). Tomar el estado atómico final\(n\) permite la posibilidad de dispersión inelástica.

Dado que la distancia\(r\) del electrón disperso desde el núcleo no tiene nada que ver con el estado atómico,\(n=0\) para la contribución nuclear, que entonces es solo dispersión de Coulomb, y\[ \int d^3r\frac{e^{i\vec{q}\cdot\vec{r}}}{r}=\frac{4\pi}{q^2}. \label{10.1.66}\]

(Para hacer esta integral, poner en un factor de convergencia\(e^{-\varepsilon r}\) luego dejar\(\varepsilon\to 0\).)

El término que involucra a los electrones atómicos es otra cuestión: para el\(i^{th}\) electrón, la integración sobre la coordenada del electrón dispersado da un factor\((4\pi/q^2)e^{i\vec{q}\cdot\vec{r}_i}\), pero la parte dura es encontrar el valor del elemento matriz de este operador entre los estados atómicos. Observe que esto es solo la transformada de Fourier del potencial electrostático de la densidad de carga del\(i^{th}\) electrón,

\( \nabla^2V_i(\vec{r}i)=4\pi\rho_i(\vec{r}_i)\)transforma a\(V_i(\vec{q})=(4\pi/q^2)\rho_i(\vec{q})\) y\(\rho_i(\vec{r})=e\delta(\vec{r}-\vec{r}_i)\) Fourier transforma a\(e(e^{i\vec{q}\cdot\vec{r}_i})\).

El factor de forma

Para la dispersión elástica, entonces, la contribución de los electrones atómicos se interpreta simplemente: su densidad de carga da lugar a un potencial por la ecuación electrostática habitual, y el electrón (rápido) es dispersado por este potencial. Para la dispersión inelástica, se evalúa la transformada de Fourier de la densidad electrónica entre diferentes estados atómicos. En ambos casos, el elemento matriz se denomina factor de forma\(F_n(\vec{q})\) para la dispersión, en realidad\(ZF_n(\vec{q})=\langle n|\sum_i e^{i\vec{q}\cdot\vec{r}_i}|0\rangle \). El factor normalizador\(Z\) se introduce de manera que para dispersión elástica,\(F_n(\vec{q})\to 1\) como\(q\to0\).

Entonces el factor de forma es un mapa de la densidad de carga en\(q\) el espacio. Mediante la medición de la velocidad de dispersión en diferentes ángulos, y el análisis de Fourier, es posible delinear la distribución de carga en el espacio ordinario. La misma técnica funciona para núcleos, y de hecho para partículas: el neutrón, por ejemplo, aunque eléctricamente neutro, tiene una distribución de carga eléctrica no trivial dentro de su volumen, revelada por la dispersión de electrones muy rápidos.

Los factores de forma más generales describen la distribución del espín, y también la dependencia del tiempo de las distribuciones de carga o giro en sistemas excitados. Todos estos pueden medirse con experimentos de dispersión diseñados adecuadamente.