3.1: Más de un grado de libertad

En general, el número de grados de libertad de un sistema es el número de coordenadas independientes requeridas para especificar la configuración del sistema. Cuantos más grados de libertad tenga el sistema, mayor será el número de formas independientes que el sistema puede moverse. Cuantos más movimientos posibles, se podría pensar, más complicado será analizar el sistema. De hecho, sin embargo, utilizando las herramientas del álgebra lineal, veremos que podemos tratar sistemas con muchos grados de libertad de una manera sencilla.

Osciladores acoplados

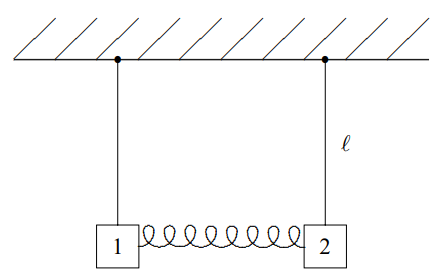
Figura\( 3.1\): Dos péndulos acoplados por un resorte.

Considera el sistema de dos péndulos que se muestra en la Figura\( 3.1\). Los péndulos consisten en varillas rígidas pivotadas en la parte superior para que oscilen sin fricción en el plano del papel. Las masas en los extremos de las varillas están acopladas por un resorte. Consideraremos el libre movimiento del sistema, sin fuerzas externas que no sean la gravedad. Este es un ejemplo clásico de dos “osciladores acoplados”. El resorte que conecta los dos osciladores es el acoplamiento. Supondremos que el resorte de la Figura\( 3.1\) está sin estirar cuando los dos péndulos están colgando recto hacia abajo, como se muestra. Entonces la configuración de equilibrio es la que se muestra en la Figura\( 3.1\). Este es un ejemplo de un sistema con dos grados de libertad, porque se requieren dos cantidades, los desplazamientos de cada uno de los dos bloques desde el equilibrio, para especificar la configuración del sistema. Por ejemplo, si las oscilaciones son pequeñas, podemos especificar la configuración dando el desplazamiento horizontal de cada uno de los dos bloques desde la posición de equilibrio.

Supongamos que el bloque 1 tiene masa\(m_{1}\), el bloque 2 tiene masa\(m_{2}\), ambos péndulos tienen longitud\(\ell\) y la constante de resorte es\(\kappa\) (letra griega kappa). Etiquete los (pequeños) desplazamientos horizontales de los bloques a la derecha,\(x_{1}\) y\(x_{2}\), como se muestra en la Figura\( 3.2\). Podríamos haber llamado a estos

Figura\( 3.2\): Dos péndulos acoplados por un resorte desplazado de sus posiciones de equilibrio.

masas y desplazamientos cualquier cosa, pero es muy conveniente usar el mismo símbolo,\(x\), con diferentes subíndices. Entonces podemos escribir la ley de Newton,\(F = m a\), en una forma compacta y útil. \[m_{j} \frac{d^{2}}{d t^{2}} x_{j}=F_{j} ,\]

for\(j\) = 1 a 2, donde\(F_{1}\) está la fuerza horizontal sobre el bloque 1 y\(F_{2}\) es la fuerza horizontal sobre el bloque 2. Debido a que hay dos valores de\(j\), (3.1) es dos ecuaciones; una para\(j\) = 1 y otra para\(j\) = 2. Estas son las dos ecuaciones de movimiento para el sistema con dos grados de libertad. A menudo nos referiremos a todas las masas, desplazamientos o fuerzas a la vez como\(m_{j}\),\(x_{j}\) o\(F_{j}\), respectivamente. Por ejemplo, diremos que\(F_{j}\) es la fuerza horizontal sobre el bloque\(j\) th. Este es un ejemplo del uso de “índices” (\(j\)es un índice) para simplificar la descripción de un sistema con más de un grado de libertad.

Cuando los bloques se mueven horizontalmente, también se moverán verticalmente, porque la longitud de los péndulos permanece fija. Debido a que el desplazamiento vertical es de segundo orden en el\(x_{j}\) s,\[y_{j} \approx \frac{x_{j}^{2}}{2} ,\]

podemos ignorarlo al pensar en la primavera. El resorte permanece aproximadamente horizontal para pequeñas oscilaciones.

Para encontrar la ecuación de movimiento para este sistema, debemos encontrar las fuerzas\(F_{j}\),, en términos de los desplazamientos,\(x_{j}\). Es la linealidad aproximada del sistema lo que nos permite hacer esto de manera útil. Las fuerzas producidas por el resorte de la ley de Hooke, y las fuerzas horizontales sobre los péndulos debido a la tensión en la cuerda (que a su vez se debe a la gravedad) son ambas funciones aproximadamente lineales de los desplazamientos para pequeños desplazamientos. Además, las fuerzas desaparecen cuando ambos desplazamientos desaparecen, porque el sistema está en equilibrio. Así, cada una de las fuerzas es algunos tiempos constantes (diferentes para cada bloque)\(x_{1}\) más algunos otros tiempos constantes\(x_{2}\). Es conveniente escribir esto de la siguiente manera:\[F_{1}=-K_{11} x_{1}-K_{12} x_{2}, \quad F_{2}=-K_{21} x_{1}-K_{22} x_{2} ,\]

o de manera más compacta,\[F_{j}=-\sum_{k=1}^{2} K_{j k} x_{k}\]

para\(j\) = 1 a 2. Hemos escrito las cuatro constantes como\(K_{11}\),\(K_{12}\),\(K_{21}\) y con el\(K_{22}\) fin de escribir la fuerza de esta manera compacta. Posteriormente, llamaremos a estas constantes los elementos matriciales de la\(K\) matriz. En esta notación, las ecuaciones de movimiento son\[m_{j} \frac{d^{2}}{d t^{2}} x_{j}=-\sum_{k=1}^{2} K_{j k} x_{k}\]

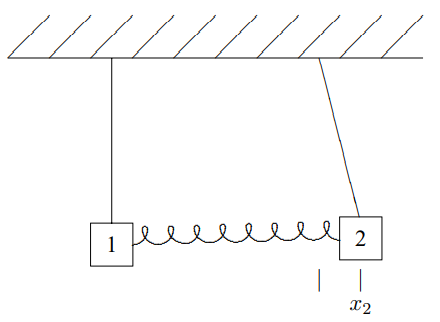
Figura\( 3.3\): Dos péndulos acoplados por un muelle con bloque 2 desplazado de una posición de equilibrio.

Debido a la linealidad del sistema, podemos encontrar las constantes,\(K_{jk}\), considerando los desplazamientos de los bloques uno a la vez. Entonces encontramos la fuerza total usando (3.4). Por ejemplo, supongamos que desplazamos el bloque 2 con el bloque 1 mantenido fijo en su posición de equilibrio y observamos las fuerzas en ambos bloques. Esto nos permitirá computar\(K_{12}\) y\(K_{22}\). El sistema con bloque dos desplazado se muestra en la Figura\( 3.3\). Las fuerzas sobre los bloques se muestran en la Figura\( 3.4\), donde\(T_{j}\) está la tensión en la cuerda de péndulo\(j\) th. \(F_{12}\)es la fuerza sobre el bloque 1 debido al desplazamiento del bloque 2. \(F_{22}\)es la fuerza sobre el bloque 2 debido al desplazamiento del bloque 2. Para pequeños desplazamientos, la fuerza restauradora del resorte es casi horizontal e igual a\(\kappa x_{2}\) la del bloque 1 y\(-\kappa x_{2}\) al bloque 2. De igual manera, en el límite de pequeño desplazamiento, la componente vertical de la fuerza de la tensión\(T_{2}\) casi cancela la fuerza gravitacional en el bloque 2,\(m_{2}g\), de manera que la componente horizontal de la tensión da una fuerza restauradora\(-x_{2} m_{2} g / \ell\) en el bloque 2. Para el bloque 1, la fuerza de la tensión\(T_{1}\) simplemente cancela la fuerza gravitacional\(m_{1}g\). Así\[F_{12} \approx \kappa x_{2}, \quad F_{22} \approx-\frac{m_{2} g x_{2}}{\ell}-\kappa x_{2},\]

y\[K_{12} \approx-\kappa, \quad K_{22} \approx \frac{m_{2} g}{\ell}+\kappa .\]

Un argumento análogo muestra que\[K_{21} \approx-\kappa, \quad K_{11} \approx \frac{m_{1} g}{\ell}+\kappa .\]

Observe que\[K_{12}=K_{21} .\]

Veremos a continuación que este es un ejemplo de una relación muy general.

Figura\( 3.4\): Las fuerzas sobre los dos bloques de la Figura\( 3.3\).

Linealidad y modos normales

3-1
Veremos en este capítulo que el movimiento más general posible de este sistema, y de cualquier sistema de osciladores de este tipo, puede descomponerse en soluciones particularmente simples, en las que todos los grados de libertad oscilan con la misma frecuencia. Estas soluciones simples se llaman “modos normales”. Los desplazamientos para la moción más general pueden escribirse como sumas de las soluciones simples. Estudiaremos cómo funciona esto en detalle más adelante, pero puede ser útil verlo primero. Un posible movimiento del sistema de dos osciladores acoplados se anima en el programa 3-1. Debajo del movimiento real, mostramos los dos movimientos simples en los que se puede descomponer el movimiento más complicado. Para este sistema, el modo normal con la frecuencia más baja es aquel en el que los desplazamientos de los dos bloques son los mismos:\[x_{1}(t)=x_{2}(t)=b_{1} \cos \left(\omega_{1} t-\theta_{1}\right) .\]

El otro modo normal es aquel en el que los desplazamientos de los dos bloques son opuestos\[x_{1}(t)=-x_{2}(t)=b_{2} \cos \left(\omega_{2} t-\theta_{2}\right) .\]

La suma de estos dos movimientos simples da el movimiento mucho más complicado que se muestra en el programa 3-1.

\(n\)Osciladores acoplados

Antes de intentar resolver las ecuaciones del movimiento, (3.5), generalicemos la discusión a sistemas con más grados de libertad. Considera la oscilación de un sistema de\(n\) partículas conectadas por varios resortes sin amortiguación. Nuestro análisis será completamente general, pero por simplicidad, hablaremos de las partículas como si estuvieran obligadas a moverse en la\(x\) dirección, para que podamos medir el desplazamiento de la partícula\(j\) th desde el equilibrio con la coordenada\(x_{j}\). Entonces la configuración de equilibrio es aquella en la que todas las\(x_{j}\) s son todas cero.

La ley de Newton\(F = ma\),, para el movimiento del sistema da\[m_{j} \frac{d^{2} x_{j}}{d t^{2}}=F_{j}\]

donde\(m_{j}\) está la masa de la partícula\(j\) th,\(F_{j}\) es la fuerza sobre ella. Debido a que el sistema es lineal, esperamos que podamos escribir la fuerza de la siguiente manera (como en (3.4)):\[F_{j}=-\sum_{k=1}^{n} K_{j k} x_{k}\]

\(j = 1\)para\(n\). La constante,\(-K_{j k}\), es la fuerza por unidad de desplazamiento de la\(j\) partícula debido a un desplazamiento\(x_{k}\) de la\(k\) ésima partícula. Tenga en cuenta que todos los\(F_{j}\) s desaparecen en equilibrio cuando todos los\(x_{j}\) s son cero. Así las ecuaciones de movimiento son\[m_{j} \frac{d^{2} x_{j}}{d t^{2}}=-\sum_{k} K_{j k} x_{k}\]

\(j = 1\)para\(n\).

Para medir\(K_{jk}\), realizar un pequeño desplazamiento,\(x_{k}\), de la partícula\(k\) th, manteniendo todas las demás partículas fijas en cero, se supone que es una posición de equilibrio. Luego mida la fuerza,\(F_{jk}\) sobre la partícula\(j\) th con solo la partícula\(k\) th desplazada. Dado que el sistema es lineal (porque está hecho de resortes o en general, siempre y cuando el desplazamiento sea lo suficientemente pequeño), la fuerza es proporcional al desplazamiento,\(x_{k}\). La relación de\(F_{jk}\) a\(x_{k}\) es\(-K_{jk}\):\[K_{j k}=-F_{j k} / x_{k} \text { when } x_{\ell}=0 \text { for } \ell \neq k .\]

Obsérvese que\(K_{jk}\) se define con un\(-\) signo, de manera que un positivo\(K\) es una fuerza que es opuesta al desplazamiento, y por lo tanto tiende a devolver el sistema al equilibrio.

Debido a que el sistema es lineal, la fuerza total debida a un desplazamiento arbitrario es la suma de las contribuciones de cada desplazamiento. Así\[F_{j}=\sum_{k} F_{j k}=-\sum_{k} K_{j k} x_{k}\]

Tratemos ahora de entender (3.9). Si consideramos sistemas sin amortiguación, las fuerzas pueden derivarse de una energía potencial,\[F_{j}=-\frac{\partial V}{\partial x_{j}} .\]

Pero luego diferenciando la ecuación (3.16) encontramos que\[K_{j k}=\frac{\partial^{2} V}{\partial x_{j} \partial x_{k}} .\]

Las diferenciaciones parciales se desplazan entre sí, por lo que la ecuación (3.18) implica\[K_{j k}=K_{k j} .\]

En palabras, la fuerza sobre la partícula\(j\) debida a un desplazamiento de la partícula\(k\) es igual a la fuerza sobre la partícula\(k\) debida al desplazamiento de la partícula\(j\).