8.2: Fuerza, Potencia e Impedancia

Cualquiera que sea la aplicación de las condiciones de contorno en el ejemplo de (8.9) debe ejercer una fuerza sobre la cuerda. Por supuesto, se requiere una fuerza horizontal para mantener la cuerda estirada, pero para pequeñas oscilaciones, esta fuerza es casi constante y aproximadamente igual a la tensión de la cuerda,\(T\). Además, no hay movimiento en la\(x\) dirección por lo que no se realiza ningún trabajo por este componente de la fuerza. La componente vertical de la fuerza es la negativa de la fuerza que produce la tensión en la cuerda. En\(x = 0\), esto es\[F_{0}=-\left.T \frac{\partial}{\partial x} \psi(x, t)\right|_{x=0} .\]

Esto se ilustra en\(Figure \text { } 8.5\).

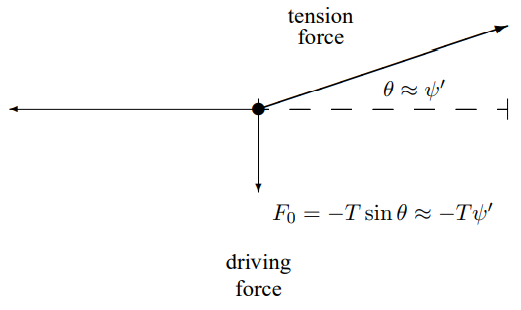
Figura\( 8.5\): La fuerza debida a una cuerda que tira en la\(+ x\) dirección.

En\(x = L\), debido a que la cuerda viene de la\(- x\) dirección, es\[F_{L}=\left.T \frac{\partial}{\partial x} \psi(x, t)\right|_{x=L} ,\]

como se ilustra en la Figura\( 8.6\).

Figura\( 8.6\): La fuerza debida a una cuerda que tira en la\(- x\) dirección.

En la oscilación forzada, el extremo de la cuerda se mueve solo en dirección transversal. Por lo tanto, la potencia suministrada por la fuerza externa en\(x = 0\), que\(\vec{F} \cdot \vec{v}\) es\[P(t)=-\left.T \frac{\partial}{\partial x} \psi(x, t)\right|_{x=0} \frac{\partial}{\partial t} \psi(0, t)\]

donde como en (2.26),\(\psi(x,t)\) es el desplazamiento real del equilibrio para la pieza de cuerda en posición horizontal\(x\). Debemos tomar primero la parte real porque el poder es una función no lineal del desplazamiento.

Para una onda estacionaria en la cuerda (o cualquier sistema sin fuerzas de fricción), la fuerza y la velocidad están\(90^{\circ}\) desfasadas. Por ejemplo, si el desplazamiento es proporcional a\(\sin \omega t\), entonces la fuerza transversal en cada extremo también es proporcional a\(\sin \omega t\). La velocidad, sin embargo, es proporcional a\(\cos \omega t\). Así, la potencia gastada por la fuerza externa es\[\propto \sin \omega t \cos \omega t=\frac{1}{2} \sin 2 \omega t .\]

Esto promedia a cero a lo largo de un medio ciclo. En promedio, no se requiere potencia para mantener la onda estacionaria en marcha (en ausencia de amortiguación).

En una onda viajera, por otro lado, la fuerza y la velocidad son proporcionales. Desde (8.15), se puede ver que\[\propto \sin \omega t \cos \omega t=\frac{1}{2} \sin 2 \omega t\]

Así\[F_{0}=Z \frac{\partial}{\partial t} \psi(0, t), \quad F_{L}=-Z \frac{\partial}{\partial t} \psi(L, t) ,\]

donde la constante\(Z\),\[Z=\frac{T k}{\omega}=\sqrt{\rho T} ,\]

se llama la “impedancia” del sistema de cuerdas. Mide la potencia requerida para producir la onda viajera. La potencia requerida en\(x = 0\) es\[P_{0}=Z\left(\frac{\partial}{\partial t} \psi(0, t)\right)^{2}=Z A^{2} \omega^{2} \sin ^{2} \omega t .\]

La potencia promedio gastada es así\[\left\langle P_{0}\right\rangle=Z A^{2} \omega^{2} / 2 .\]

La energía gastada en\(x = 0\) para producir la onda viajera es cedida por la cuerda en\(x = L\), porque la potencia requerida en\(L\) es\[P_{L}=-Z\left(\frac{\partial}{\partial t} \psi(L, t)\right)^{2}=-Z A^{2} \omega^{2} \cos ^{2} \omega t .\]

Si las condiciones límite fueran tales que las olas viajeras iban en sentido contrario, la fuerza en las derivaciones anteriores tendría el signo opuesto de (8.20). Por lo tanto, siempre se requiere la potencia positiva para producir la onda y se requiere la potencia negativa para absorberla. Puede parecer extraño que la potencia alimentada a la ola en (8.23) y la potencia cedida por la onda en (8.25) no sean exactamente iguales y opuestas. La suma desaparece en promedio, pero oscila con el tiempo. La razón es que la longitud del sistema no es un número integral de longitudes de onda. Esto permite que la energía almacenada en el sistema, la suma de cinética y potencial, oscile en función del tiempo.

Tenga en cuenta que la fuerza requerida para absorber una onda viajera, en (8.21), es negativa y proporcional a la velocidad. Esta es una fuerza de fricción típica. Así, una onda viajera puede ser absorbida completamente por una fuerza de fricción (o una resistencia) con exactamente la relación correcta de fuerza a velocidad. Si la impedancia del “dashpot” (como se llama tal resistencia) no es exactamente la misma que la de la cuerda, habrá cierta reflexión. Volveremos a esto en el próximo capítulo.

Impedancia compleja

Para la cuerda estirada, un sistema para el cual la relación de dispersión es equivalente a la ecuación de onda, (6.4), la fuerza sobre el sistema y la velocidad de desplazamiento,\(\frac{\partial}{\partial t} \psi\), son proporcionales para cualquier onda viajera. ¹ En general, esto no es cierto. Por ejemplo, consideremos la cuerda con cuentas de Figura\( 5.4\) estirada desde\(x = 0\) hasta alguna grande\(x\). Supongamos además que hay una onda viajera en el sistema de la forma,\[\psi(x, t)=A \cos (k x-\omega t) ,\]

ilustrado en la Figura\( 8.7\). ² La línea punteada es la posición de equilibrio de la cuerda.

Figura\( 8.7\): Una instantánea de una onda viajera en una cuerda con cuentas.

Siempre\(k\) y cuando y\(\omega\) estén relacionados por la relación de dispersión, (5.39), entonces (8.26) es una solución a la ecuación del movimiento. La fuerza transversal externa\(x = 0\) requerida para producir la onda viajera está relacionada con la diferencia entre el desplazamiento del primer bloque y el desplazamiento del extremo en\(x = 0\) (ver figura 5.5). Es\[F_{0}=\frac{T A}{a}(\cos (\omega t-k a)-\cos \omega t) .\]

Esto es aproximadamente proporcional a la velocidad solo si\(ka\) es muy pequeña, de manera que el lado derecho de (8.27) se puede expandir en una serie de Taylor. Así, en este caso, y en general para un sistema discreto, no podemos definir la impedancia simplemente como en (8.21).

Sin embargo, supongamos que en lugar de las olas viajeras reales, (8.26), consideramos una onda viajera armónica compleja con tiempo y espacio irreducibles de la forma\[\psi(x, t)=A e^{-i(\omega t-k x)} .\]

Entonces por lo irreducible on\(t\) y\(x\) (que viene de la invarianza de la traducción), sabemos inmediatamente que tanto la fuerza como la\(t\) derivada de\(\psi\) son proporcionales a\(\psi\). Para una solución irreducible, todo es proporcional a\(e^{-i(\omega t-k x)}\). Así también son proporcionales entre sí, y podemos definir la impedancia,\[F=-Z(k) \frac{\partial}{\partial t} \psi(x, t)=i \omega A Z(k) e^{-i(\omega t-k x)} .\]

Por ejemplo, para la cuerda con cuentas, si reemplazamos la solución real, (8.26), con la solución compleja irreducible, (8.28), la fuerza se vuelve\[F_{0}=\frac{T A}{a}\left(e^{-i(\omega t-k a)}-e^{-i \omega t}\right)=\frac{T A}{a}\left(e^{i k a}-1\right) e^{-i \omega t} .\]

Así de (8.29), la impedancia,\(Z(k)\), es\[Z(k)=\frac{T}{\omega a} \frac{e^{i k a}-1}{i}=\frac{2 T}{a} e^{i k a / 2} \frac{\sin \frac{k a}{2}}{\omega} .\]

Usando la relación de dispersión, (5.39), podemos escribir esto como\[Z(k)=e^{i k a / 2} \sqrt{\frac{m T}{a}} .\]

La impedancia,\(Z(k)\), definida por (8.29) es, en general, compleja y\(k\) dependiente. Sin embargo, podemos encontrar la potencia promedio requerida para producir la ola. Debido a que la potencia es una función no lineal del desplazamiento, primero debemos tomar las partes reales de la velocidad compleja y la fuerza compleja antes de calcular la potencia, como en (2.26). Para complejo arbitrario\(A=|A| e^{i \phi}\),\ [\ begin {reunió}
v=\ omega|a|\ sin (\ omega t-k x-\ phi),\\
F =(\ nombreoperador {Im} Z (k))\ omega|a|\ cos (\ omega t-k x-\ phi) + (\ nombreoperador {Re} Z (k))\ omega|a|\ sin (\ t-k x-\ phi),
\ fin {reunidos}\]

donde hemos puesto la fase de\(A\) en las\(\sin\) funciones\(\cos\) y (ver (1.96) - (1.98)) para dejar claro que sólo el valor absoluto de las\(A\) materias para el poder promedio. Entonces, como en (2.26), sólo el\(\sin^{2}\) término contribuye al poder promediado en el tiempo, que es\[\frac{1}{2}(\operatorname{Re} Z) \omega^{2}|A|^{2} .\]

______________________
¹ Veremos esto en detalle en el capítulo 10.
² Para una animación de una onda viajera en un sistema similar, consulte el programa 8-6. El sistema que se muestra en este programa tiene las cuentas en resortes, así como en una cuerda. No obstante, la forma de la ola viajera es la misma. Sólo la relación de dispersión es diferente.