8.3: Luz

Las ondas de luz, como las ondas sonoras que discutimos en el capítulo anterior, son cosas inherentemente tridimensionales. Sin embargo, como con el sonido, podemos decir mucho sobre la luz que es más o menos independiente de los detalles tridimensionales.

Ondas Planas

Hay una manera sencilla de concentrarse en una sola dimensión. Es decir, buscar soluciones en las que las otras dos dimensiones no entren en absoluto. Considere las ecuaciones de Maxwell en el espacio libre, en términos de los campos vectoriales,\(\vec{E}\) y\(\vec{B}\) describiendo los campos eléctrico y magnético. \ [\ begin {alineado}
&\ frac {\ parcial E_ {y}} {\ parcial x} -\ frac {\ parcial E_ {x}} {\ parcial y} =-\ frac {\ parcial B_ {z}} {\ parcial t}\\
&\ frac {\ parcial E_ {z}} {\ parcial y} -\ frac {\ parcial E_ {y}} {\ z parcial} =-\ frac {\ parcial B_ {x}} {\ t parcial}\\
&\ frac {\ parcial E_ {x}} {\ z parcial} -\ frac {\ parcial E_ {z}} {\ parcial x} =-\ frac {\ parcial B_ {y}} {\ t parcial}
\ final {alineado}\]

\ [\ begin {alineado}
&\ frac {\ parcial B_ {y}} {\ parcial x} -\ frac {\ parcial B_ {x}} {\ parcial y} =\ mu_ {0}\ epsilon_ {0}\ frac {\ parcial E_ {z}} {\ parcial t}\\
&\ frac {\ parcial B_ {z} {parcial}} -\ frac {\ parcial B_ {y}} {\ z parcial} =\ mu_ {0}\ épsilon_ {0}\ frac {\ parcial E_ {x}} {\ t parcial}\\
&\ frac {\ parcial B_ {x}} {\ parcial z} -\ frac {\ parcial B_ {z}} {\ parcial x} =\ mu_ {0}\ épsilon_ {0}\ frac {\ parcial E_ {y}} {\ t parcial}
\ final {alineado}\]

\ [\ begin {alineado}
&\ frac {\ parcial E_ {x}} {\ parcial x} +\ frac {\ parcial E_ {y}} {\ parcial y} +\ frac {\ parcial E_ {z}} {\ z parcial} =0\\
&\ frac {\ parcial B_ {x}} {\ parcial x} +\ frac {\ parcial B_ y {}} {\ parcial y} +\ frac {\ parcial B_ {z}} {\ z parcial} =0
\ final {alineado}\]

donde\(\epsilon_{0}\) y\(\mu_{0}\) son dos constantes llamadas permitividad y permeabilidad del espacio vacío. ³ Busquemos soluciones a estas ecuaciones diferenciales parciales que involucren sólo funciones de\(z\) y\(t\). En este caso, las cosas se simplifican para:\[0=-\frac{\partial B_{z}}{\partial t}, \quad-\frac{\partial E_{y}}{\partial z}=-\frac{\partial B_{x}}{\partial t}, \quad \frac{\partial E_{x}}{\partial z}=-\frac{\partial B_{y}}{\partial t} ,\]

\[0=\mu_{0} \epsilon_{0} \frac{\partial E_{z}}{\partial t}, \quad-\frac{\partial B_{y}}{\partial z}=\mu_{0} \epsilon_{0} \frac{\partial E_{x}}{\partial t}, \quad \frac{\partial B_{x}}{\partial z}=\mu_{0} \epsilon_{0} \frac{\partial E_{y}}{\partial t} ,\]

\[\frac{\partial E_{z}}{\partial z}=0, \quad \frac{\partial B_{z}}{\partial z}=0 .\]

Estas ecuaciones implican eso\(E_{z}\) y\(B_{z}\) son independientes de\(z\) y\(t\). Ya que ya asumimos que sólo dependen de\(z\) y\(t\), esto quiere decir que son constantes. Los ignoraremos porque nos interesan las soluciones con no trivial\(z\) y\(t\) dependencia. Eso deja los\(y\) componentes\(x\) y, satisfactorios (8.38) y (8.39).

Entonces, porque (8.38) y (8.39) son invariantes bajo traducciones en\(z\) y\(t\), esperamos soluciones exponenciales complejas, en las que todos los componentes son proporcionales a\[e^{i(\pm k z-\omega t)},\]

\[E_{x}(z, t)=\varepsilon_{x}^{\pm} e^{i(\pm k z-\omega t)}, \quad E_{y}(z, t)=\varepsilon_{y}^{\pm} e^{i(\pm k z-\omega t)} ,\]

\[B_{x}(z, t)=\beta_{x}^{\pm} e^{i(\pm k z-\omega t)}, \quad B_{y}(z, t)=\beta_{y}^{\pm} e^{i(\pm k z-\omega t)} ,\]

La sustitución directa de (8.42) y (8.43) en (8.38) y (8.39) da\[\mp k \varepsilon_{y}^{\pm}=\omega \beta_{x}^{\pm}, \quad \pm k \varepsilon_{x}^{\pm}=\omega \beta_{y}^{\pm},\]

\[\mp k \beta_{y}^{\pm}=-\mu_{0} \epsilon_{0} \omega \varepsilon_{x}^{\pm}, \quad \pm k \beta_{x}^{\pm}=-\mu_{0} \epsilon_{0} \omega \varepsilon_{y}^{\pm} .\]

Como es habitual, hemos escrito la ola con la irreducible dependencia del tiempo,\(e^{-i \omega t}\). Para obtener los campos eléctricos y magnéticos reales, tomamos la parte real de (8.42) y (8.43). Esto funciona porque las ecuaciones de Maxwell son lineales en los campos eléctrico y magnético. Las amplitudes\(\varepsilon_{x}^{\pm}\), etc, pueden ser complejas.

De (8.44) y (8.45), se ve que\(\varepsilon_{y}^{\pm}\) está relacionado con\(\beta_{x}^{\pm}\) y\(\varepsilon_{x}^{\pm}\) está relacionado con\(\beta_{y}^{\pm}\). Para cada relación, hay dos ecuaciones lineales simultáneas homogéneas en las dos incógnitas. Son consistentes sólo si la relación de los coeficientes es la misma, lo que implica una relación entre\(k\) y\(\omega\),\[k^{2}=\mu_{0} \epsilon_{0} \omega^{2} .\]

Esta es una relación de dispersión,\[\omega^{2}=c^{2} k^{2}=\frac{1}{\mu_{0} \epsilon_{0}} k^{2} .\]

La velocidad de fase\(c\),, es la velocidad de la luz en vacío (¡tendremos más que decir sobre esto en los capítulos 10 y 11!).

Una vez satisfecho (8.47), podemos resolver para el\(\beta^{\pm}\) en términos de\(\varepsilon^{\pm}\):\[\beta_{y}^{\pm}=\pm \frac{1}{c} \varepsilon_{x}^{\pm}, \quad \beta_{x}^{\pm}=\mp \frac{1}{c} \varepsilon_{y}^{\pm} .\]

Estas soluciones a las ecuaciones de Maxwell en el espacio libre son las ondas electromagnéticas o las ondas de luz. Estas soluciones simples, dependiendo únicamente\(z\) y\(t\) son un ejemplo de soluciones de onda plana. El nombre es apropiado porque los campos eléctricos y magnéticos en la onda tienen el mismo valor en todas partes en cada plano de constante\(z\), para cualquier tiempo fijo,\(t\). Estos planos se propagan en la\(\pm z\) dirección a la velocidad de fase,\(c\).

En general, las ondas electromagnéticas pueden propagarse en cualquier dirección en el espacio tridimensional. No obstante, los campos eléctricos y magnéticos que componen la onda son siempre perpendiculares a la dirección en la que se desplaza la onda y perpendiculares entre sí.

El tratamiento de las ondas electromagnéticas de onda plana que viajan en la\(z\) dirección es análogo a nuestro tratamiento del sonido en el capítulo 7. Ahí, también, la ola sólo dependía de\(z\). Sin embargo, las ondas electromagnéticas son un poco más complicadas porque el fenómeno de las ondas depende tanto del campo eléctrico como del magnético. La razón por la que hemos pospuesto hasta ahora la discusión de las ondas electromagnéticas, a pesar de que son uno de los ejemplos más importantes de fenómenos de onda, es que las relaciones, (8.48), entre los campos eléctrico y magnético dependen de la dirección en la que se desplaza la onda (¡el\(\pm\) signo!). Es mucho más fácil anotar las soluciones para las olas viajeras que para las olas estacionarias. Incluso para las ondas planas viajeras simples que hemos descrito que dependen solo de\(z\) y\(t\), esta relación entre\(\vec{E}\) y\(\vec{B}\) y la dirección de la onda depende de las propiedades tridimensionales de las ecuaciones de Maxwell. Discutiremos estos temas con mucho más detalle en los capítulos 11 y 12.

Interferómetros

Una de las características maravillosas de las ondas de luz es que es relativamente fácil dividirlas y volver a montarlas. Esta característica se utiliza en muchos dispositivos ópticos, uno de los

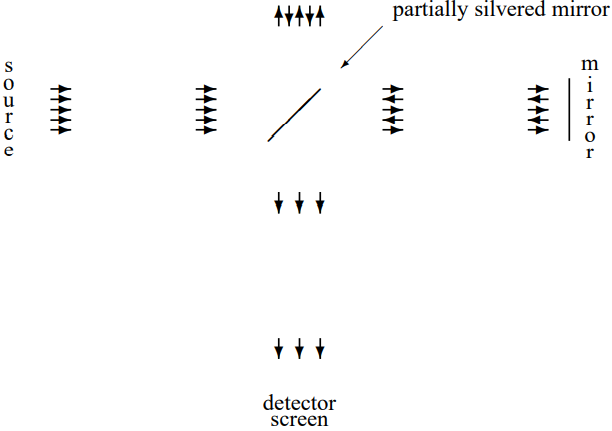
Figura\( 8.8\): Diagrama esquemático de un interferómetro Michelson.

que es un “interferómetro”, una versión del cual (el interferómetro Michelson) se muestra en forma esquemática en la Figura\( 8.8\). Una fuente produce una onda plana (como discutiremos en el capítulo 13, no puede ser toda una onda plana, pero no importa eso por ahora). El espejo parcialmente plateado sirve como un “divisor de haz” al permitir que pase parte de la luz, mientras refleja el resto. Después los espejos en la parte superior y la derecha reflejan las vigas hacia atrás. Entonces el espejo parcialmente plateado sirve como un “reensamblador de haz”, combinando los haces desde la parte superior y la derecha en un solo haz que viaja a la pantalla del detector donde se mide la intensidad del haz (proporcional al cuadrado del campo eléctrico). Lo importante es que la onda de luz que llega a la pantalla del detector es la suma de dos componentes que son coherentes y sin embargo han recorrido caminos diferentes. Lo que significa “coherente” en este contexto no sólo es que la frecuencia es la misma, sino que la fase de las ondas está correlacionada. En este caso, eso sucede simplemente porque los dos componentes que llegan a la pantalla surgen de la misma onda plana entrante.

Ahora la intensidad de la luz que llega a la pantalla depende de la longitud relativa de los dos caminos. Diferentes longitudes de trayectoria producirán diferentes fases. Si los dos componentes están en fase, las amplitudes se sumarán y la pantalla será brillante. A esto se le llama “interferencia constructiva”. Si los dos componentes están\(180^{\circ}\) desfasados, las amplitudes restarán y la pantalla estará oscura. Habrá lo que se llama “interferencia destructiva”.

Esto suena bastante trivial, y de hecho lo es (al menos para las ondas electromagnéticas clásicas), pero también es extremadamente útil, porque proporciona una medida muy sensible de los cambios de la longitud de los caminos. En particular, si uno de los espejos se mueve una distancia\(d\) (podría ser parte de una configuración experimental diseñada para detectar pequeños movimientos, por ejemplo), la fase relativa de los dos componentes que llegan a la pantalla cambia por\(2kd\) dónde\(k\) está el número de onda angular de la onda plana, porque la longitud de la trayectoria de la onda reflejada ha cambiado en\(2d\). Así, cada vez que\(d\) cambia un cuarto de la longitud de onda de la luz, la pantalla pasa de brillante a oscura, o viceversa.

Esta es una forma muy útil de medir pequeños cambios de distancia. En la práctica, el haz entrante no es exactamente una onda plana (¡eso, como veremos en detalle más adelante, requeriría un experimento infinito!) , por lo que la intensidad de la luz no es uniforme sobre la pantalla. En cambio, hay áreas claras y áreas oscuras conocidas como “franjas”. A medida que se mueve el espejo, las franjas se mueven, y se pueden contar las franjas que pasan por un punto determinado para realizar un seguimiento del número de cambios de brillante a oscuro.

Interferencia cuántica

Hay otra ola de pensar en el interferómetro que lo hace parecer mucho menos trivial. Como discutiremos varias veces en este libro, y aprenderás más sobre cuando estudies la mecánica cuántica, la luz no es solo una onda. También se compone de partículas individuales de luz llamadas fotones. No te das cuenta de esto a menos que bajes la intensidad de la onda de luz. Pero de hecho, puedes bajar tanto la intensidad que puedes detectar fotones individuales golpeando la pantalla. Ahora no está tan claro lo que está pasando. Un fotón individual no puede dividirse en dos partes en el divisor de haz y el reensamblador de haz. Como veremos más adelante, la energía del fotón está determinada por la frecuencia de la luz. No se puede dividir. Se podría pensar, por lo tanto, que el fotón individual tendría que ir de una manera u otra. Pero entonces, ¿cómo se puede obtener una interferencia entre los dos caminos? No hay respuesta a esta pregunta que tiene “sentido” en la física clásica de las partículas. Sin embargo, cuando se realiza el experimento, el número de fotones que llegan a la pantalla depende de la diferencia de longitudes entre los dos caminos ¡en la forma que esperas de la descripción de la onda! La probabilidad de que un fotón llegue a un punto determinado en la pantalla es proporcional a la intensidad de la onda clásica correspondiente. Si las longitudes de las trayectorias producen interferencias destructivas, no pasan fotones. No solo eso, sino que se pueden hacer experimentos similares con otras partículas, ¡como los neutrones! A lo mejor la interferencia no es tan trivial después de todo.

___________________________
³ Véase, por ejemplo, Purcell, capítulo 9.