8.4: Líneas de Transmisión

Hemos visto que un sistema invariante de traslación de inductores y capacitores puede transportar ondas. Preguntemos qué sucede cuando tomamos el límite continuo de tal sistema. Esto dará una interesante visión de las ondas electromagnéticas. La relación de dispersión para el sistema de la Figura\( 5.23\) viene dada por (5.75),\[\omega^{2}=\frac{4}{L_{a} C_{a}} \sin ^{2} \frac{k a}{2} .\]

donde\(L_{a}\) y\(C_{a}\) son la inductancia y capacitancia de los inductores y capacitores para el sistema con separación\(a\) entre partes vecinas. Para tomar el límite de continuum, debemos reemplazar la inductancia y capacitancia,\(L_{a}\) y\(C_{a}\), por cantidades que esperamos que tengan límites finitos como\(a \rightarrow 0\). Esperamos de la analogía, (5.69), entre\(LC\) circuitos y sistemas de resortes y masas, y de la discusión al inicio del capítulo 7 sobre el límite continuo del sistema de masas y resortes que las cantidades relevantes serán:\ [\ begin {aligned}
&\ rho_ {L}\ rightarrow\ frac { L_ {a}} {a}\ quad\ texto {inductancia por unidad de longitud}\\
&K_ {a} a\ fila derecha\ frac {a} {C_ {a}}\ quad\ texto {capacitancia por unidad de longitud}
\ end {alineado}\]

Estas dos cantidades se pueden calcular directamente a partir de la inductancia y capacitancia de una longitud finita\(\ell\),, del sistema que contiene muchas unidades individuales. Las inductancias están conectadas en serie por lo que las inductancias individuales se suman para dar la inductancia total. Así, si la longitud\(\ell\) es\(na\) tal que si el sistema finito contiene\(n\) inductores, la inductancia total es\(L = n L_{a}\). Entonces\[\frac{L}{\ell}=\frac{L_{a}}{a}\]

Las capacitancias funcionan de la misma manera porque están conectadas en paralelo, y las capacitancias paralelas se suman. Por lo tanto\[\frac{C}{\ell}=\frac{C_{a}}{a} .\]

Por lo tanto, al tomar el límite a partir\(a \rightarrow 0\) del (8.49), podemos escribir\[L_{a}=a \frac{L}{\ell}, \quad C_{a}=a \frac{C}{\ell} .\]

Esto da la siguiente relación de dispersión:\[\omega^{2}=\frac{\ell^{2}}{L C} \frac{4 \sin ^{2} \frac{k a}{2}}{a^{2}} \rightarrow \frac{\ell^{2}}{L C} k^{2} .\]

Un sistema continuo como este con inductancia fija y capacitancia por unidad de longitud se llama línea de transmisión. Llamaremos a (8.54) la relación de dispersión para una línea de transmisión sin resistencia. Una línea de transmisión se puede utilizar para enviar ondas eléctricas, así como una cadena continua transmite ondas mecánicas. En el sistema continuo, la variable de desplazamiento, la carga desplazada, se convierte en una función de posición a lo largo de la línea de transmisión. Si la línea de transmisión se estira en la\(z\) dirección, podemos describir las cargas en la línea de transmisión mediante una función\(Q(z,t)\) que es la carga que ha sido desplazada a través del punto de la línea de transmisión\(z\) en el momento\(t\). La derivada de tiempo de\(Q(z,t)\) es la corriente en el momento\(z\) y momento\(t\):\[I(z, t)=\frac{\partial Q(z, t)}{\partial t} .\]

Línea de transmisión de placa paralela

Vale la pena elaborar un ejemplo particular de una línea de transmisión. El ejemplo que vamos a utilizar es de dos largas tiras conductoras paralelas. Imagínese un sistema infinito en el que las tiras se estiran paralelas entre sí en planos de constante\(y\), yendo al infinito en la\(z\) dirección. Supongamos que las tiras son lo suficientemente delgadas como para que podamos descuidar su grosor. Supongamos además que el ancho de las tiras\(w\),, es mucho mayor que la separación,\(s\). Una sección transversal de esta línea de transmisión en el\(x - y\) plano se muestra en la Figura\( 8.9\). En la figura, la\(z\) dirección es fuera del plano del papel, hacia ti. Haremos un seguimiento del movimiento de las cargas en el conductor superior y asumiremos que el conductor inferior está conectado a tierra (con voltaje fijo en\(V = 0\)).

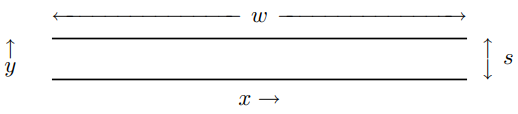
Figura\( 8.9\): Sección transversal de una línea de transmisión en el\(x - y\) plano.

Encontraremos la relación de dispersión de la línea de transmisión calculando la capacitancia e inductancia de una parte de la línea de longitud\(\ell\). Será útil hacer esto utilizando consideraciones energéticas. Supongamos que hay una carga,\(Q\), uniformemente distribuida sobre la placa superior del condensador, y una corriente,\(I\), que fluye uniformemente fuera del\(x - y\) plano en la\(z\) dirección a lo largo del conductor superior (y de vuelta al plano a lo largo del conductor inferior). La energía almacenada en la longitud,\(\ell\), de la línea de transmisión es entonces\[\frac{1}{2 C} Q^{2}+\frac{1}{2} L I^{2} ,\]

donde\(C\) y\(L\) son la capacitancia y la inductancia. ⁴

La energía se almacena en realidad en los campos eléctricos y magnéticos producidos por la carga y la corriente. En esta configuración, los campos eléctrico y magnético se encuentran casi en su totalidad entre las dos placas de la pieza de la línea de transmisión. Si\(Q\) y\(I\) son positivos, los campos eléctrico y magnético son como se muestra en la Figura\( 8.10\) y Figura\( 8.11\). En la Figura\( 8.10\), la línea punteada es una sección transversal de una región en forma de caja que se puede utilizar para calcular el campo eléctrico, utilizando la ley de Gauss. En la Figura\( 8.11\), la trayectoria punteada se puede utilizar para calcular el campo magnético, utilizando la ley de Ampere. Los campos eléctrico y magnético son aproximadamente constantes entre las bandas, pero rápidamente caen a cerca de cero afuera.

Figura\( 8.10\): El campo eléctrico debido a la carga en la línea de transmisión.

Figura\( 8.11\): El campo magnético debido a la corriente en la línea de transmisión.

La densidad de carga en la placa superior es aproximadamente uniforme y dada por la carga total dividida por el área\(w \ell\),\[\sigma \approx \frac{Q}{w \ell} .\]

Entonces podemos aplicar la ley de Gauss a una pequeña región en forma de caja, una sección transversal de la cual se muestra en la Figura\( 8.10\) y concluir que el campo eléctrico en su interior viene dado por\[E_{y} \approx-\frac{Q}{\epsilon_{0} w \ell}\]

Por lo tanto, la densidad de energía almacenada en el campo eléctrico entre las placas es\[u_{E}=\frac{\epsilon_{0}}{2} E^{2} \approx \frac{Q^{2}}{2 \epsilon_{0} w^{2} \ell^{2}} .\]

La energía total almacenada en el campo eléctrico se obtiene multiplicando\(u_{E}\) por el volumen entre las placas, rindiendo\[\frac{1}{2} \frac{s}{\epsilon_{0} w \ell} Q^{2}\]

así (comparando con (8.56))\[C=\frac{\epsilon_{0} w \ell}{s} .\]

Podemos calcular la inductancia de manera similar. La ley de Ampere, aplicada a una trayectoria que encierra el conductor superior (como se muestra en la figura 8.11) da\[B_{x} \approx \frac{\mu_{0} I}{w} .\]

Por lo tanto, la densidad de energía almacenada en el campo magnético entre las placas es\[u_{B}=\frac{1}{2 \mu_{0}} B^{2} \approx \frac{\mu_{0} I^{2}}{2 w^{2}} .\]

La energía total almacenada en el campo magnético se obtiene multiplicando\(u_{B}\) por el volumen entre las placas, rindiendo\[\frac{1}{2} \frac{\mu_{0} s \ell}{w} I^{2}\]

así (comparando con (8.56))\[L=\frac{\mu_{0} s \ell}{w} .\]

Ahora podemos poner (8.61) y (8.65) en (8.54) para obtener la relación de dispersión para esta línea de transmisión:\[\omega^{2}=\frac{1}{\mu_{0} \epsilon_{0}} k^{2}=c^{2} k^{2} ,\]

donde\(c\) esta la velocidad de la luz!

Ondas en la Línea de Transmisión

La relación de dispersión, (8.66), se parece sospechosamente a la relación de dispersión para ondas electromagnéticas. De hecho, los campos eléctrico y magnético entre las bandas de la línea de transmisión tienen exactamente la forma de una onda electromagnética. Para ver esto explícitamente, veamos una onda viajera en la línea de transmisión, y consideremos la carga,\(Q(z,t)\), desplazada a través\(z\), con lo irreducible complejo exponencial\(z\) y\(t\) dependencia,\[Q(z, t)=q e^{i(k z-\omega t)} .\]

Esta ola está viajando en la\(z\) dirección positiva, hacia ti en el diagrama de la Figura\( 8.9\).

En cualquier momento\(t\) y posición fijos\(z\), los campos eléctricos y magnéticos dentro de la línea de transmisión se ven como se muestra en la Figura\( 8.10\) y Figura\( 8.11\) (o ambos pueden apuntar en la dirección opuesta). Podemos encontrar el campo magnético tal como lo hicimos anteriormente, porque la corriente en cualquier punto a lo largo de la línea viene dada por (8.55), por lo que\[B_{x}(z, t) \approx \frac{\mu_{0} I(z, t)}{w}=\frac{\mu_{0}}{w} \frac{\partial}{\partial t} Q(z, t)=-i \frac{\mu_{0} \omega q}{w} e^{i(k z-\omega t)} .\]

Para encontrar el campo eléctrico en función de\(z\) y\(t\), necesitamos la densidad de carga a lo largo de la línea. Una vez que tenemos eso, podemos encontrar el campo eléctrico usando la ley de Gauss, como arriba. Una densidad de carga distinta de cero resulta si la cantidad de carga desplazada cambia en función de\(z\). Es más fácil encontrar la densidad de carga volviendo al sistema discreto discutido en el capítulo 5, y a (5.72). En el lenguaje en el que etiquetamos las partes del sistema por sus posiciones, la carga,\(q_{j}\), en el sistema discreto se convierte en\(q(z,t)\) dónde\(z = j a\). Como\(a \rightarrow 0\), esto corresponde a una densidad de carga lineal a lo largo de la línea de transmisión de\[\rho(z, t)=\frac{q(z, t)}{a} .\]

En este lenguaje, (5.72) se convierte\[q(z, t)=Q(z, t)-Q(z+a, t) ,\]

donde\(Q(z,t)\) es la carga desplazada a través del inductor una posición\(z\) en el momento\(t\). Combinando (8.69) y (8.70) da\[\rho(z, l)=\frac{Q(z, t)-Q(z+a, t)}{a} .\]

Tomando el límite como\(a \rightarrow 0\) da\[\rho(z, t)=-\frac{\partial}{\partial z} Q(z, t)=-i k q e^{i(k z-\omega t)} .\]

Esta densidad de carga lineal se extiende sobre el ancho de la banda superior en la línea de transmisión, dando una densidad de carga superficial de\[\sigma(z, t)=\frac{\rho(z, t)}{w}=-i \frac{k q}{w} e^{i(k z-\omega t)} .\]

Ahora el campo eléctrico de la ley de Gauss es\[E_{y}=-\frac{\sigma(z, t)}{\epsilon_{0}}=i \frac{k q}{\epsilon_{0} w} e^{i(k z-\omega t)} .\]

Al comparar (8.68) con (8.74), se puede ver que (8.45) está satisfecho, de manera que este par de campos eléctricos y magnéticos forman parte de una onda plana electromagnética itinerante.

Lo que está sucediendo aquí es que el papel de las cargas y corrientes en las franjas de la línea de transmisión es confinar las ondas electromagnéticas. Sin los conductores sería imposible producir una pieza de una onda plana, como veremos con mucho más detalle en el capítulo 13.

En tanto, tenga en cuenta que el modo con\(\omega = 0\) y\(k = 0\) debe ser tratado con cuidado, como con el\(\omega = k = 0\) modo de la cuerda con cuentas discutida en el capítulo 5. El modo en el que la carga desplazada es proporcional a\(z\) (ver (5.41)) describe una situación en la que se carga toda la línea de transmisión infinita. Esto no es muy interesante en el caso finito. Sin embargo, es importante el modo que es independiente\(z\), pero que aumenta con el tiempo,\(t\) proporcional a. Esto describe la situación en la que fluye una corriente constante a través de los conductores. Dentro de la línea de transmisión, en este caso, se encuentra un campo magnético constante.

____________________
⁴ Véase Haliday y Resnick, parte 2.