13.10:13-8- Holografía

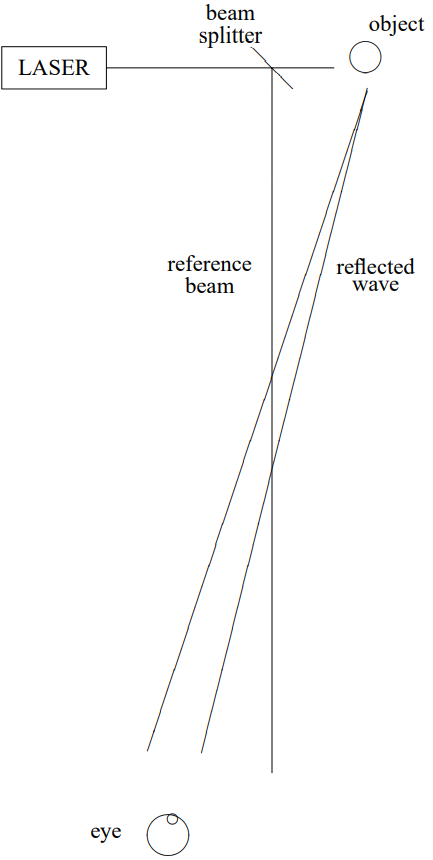
Nada nos impide hacer el análisis de un patrón de difracción desde una función más complicada,\(f(x, y)\), que la discutida en (13.16). Un holograma es tal patrón de difracción. Una de las versiones más simples de un holograma es aquella en la que un objeto es iluminado por un láser, que proporciona esencialmente una onda plana. La luz reflejada, y una parte del rayo láser (extraído por alguna técnica de división de haz) inciden sobre una placa fotográfica en ángulos ligeramente diferentes, como se muestra esquemáticamente en la Figura\( 13.31\). El incidente de onda en la placa fotográfica tiene la forma\[e^{-i \omega t}\left(e^{i k z}+\int d k_{x} d k_{y} C\left(k_{x}, k_{y}\right) e^{i \vec{k} \cdot \vec{r}}\right)\]

donde\[k=|\vec{k}|=\omega / v.\]

(13.127) describe las dos partes coherentes de la onda de luz incidente en la placa fotográfica. Por simplicidad, asumiremos que la señal en la que realmente nos interesa, la onda reflejada con transformada de Fourier\(C(k_{x}, k_{y})\), es pequeña en comparación con la onda de referencia\(e^{i k z}\). Esta señal es lo que veríamos si la placa fotográfica fuera quitada y colocáramos

Figura\( 13.31\): Realización de un holograma.

nuestros ojos en la trayectoria de la onda reflejada, pero fuera de la trayectoria del rayo láser, como se muestra en la Figura\( 13.32\).

Figura\( 13.32\): Visualización del objeto.

La placa fotográfica (asumiremos que está en\(z\) = 0) registra solo la intensidad de la onda total, proporcional a\[1+2 \operatorname{Re} \int d k_{x} d k_{y} C\left(k_{x}, k_{y}\right) e^{i\left(k_{x} x+k_{y} y\right)}+\mathcal{O}\left(C^{2}\right)\]

Dejaremos de lado los términos del orden\(C^{2}\), asumiendo que eso\(C\) es pequeño, aunque podremos ver más adelante que en realidad no van a hacer ninguna diferencia aunque\(C\) sea grande. Si ahora hacemos un deslizamiento positivo de la placa y brillamos a través de ella un rayo láser con la misma frecuencia\(\omega\),, la onda “pasa” donde la intensidad de la luz en la placa era grande y se absorbe donde la intensidad era pequeña. Así tenemos un problema de oscilación forzada exactamente del tipo que discutimos anteriormente, con (13.129) jugando el papel de\(f(x, y)\). La solución para\(z > 0\) (de (13.19) - (13.24)) es e^ {-i\ omega t}\ left (e^ {i k z} +\ int d k_ {x} d k_ {y} C\ left (k_ {x}, k_ {y}\ right) e^ {i\ vec {k}\ cdot\ vec {r}} +\ text {c.c.}\ derecha)\]

donde c.c. es la onda conjugada compleja obtenida tomando el conjugado complejo de la señal y cambiando el signo de la\(z\) dependencia para obtener una onda viajando en la\(+z\) dirección. Lo importante a tener en cuenta sobre la onda conjugada compleja es que representa un haz que viaja en una dirección diferente ya sea de la señal o del haz de referencia, debido a que la conjugación compleja ha cambiado el signo de\(k_{x}\) y\(k_{y}\).

El sistema resultante se muestra esquemáticamente en la Figura\( 13.33\). Tu ojo ve una versión reconstruida de la onda reflejada que habrías visto sin la placa fotográfica, como en (13.32). Tenga en cuenta que ni el haz de referencia ni el haz conjugado complejo se interponen en tu visión, porque se apagan en ángulos ligeramente diferentes. Esto es un holograma. Debido a que no es una imagen sino una reconstrucción de la onda real que habrías visto en (13.32), tiene la sorprendente propiedad de tridimensionalidad que hace que un holograma sea llamativo.

Figura\( 13.33\): Visualización de la imagen holográfica.

Uno podría preguntarse por qué elegimos el ángulo entre el haz de referencia y la señal para que sea pequeño. Un ángulo grande tendría la ventaja de sacar el haz de referencia más lejos del camino, pero tendría una desventaja importante. Considera el patrón de intensidad en la placa fotográfica que registra el holograma. Es un patrón oscilante con un número de onda típico dado por el valor típico de\(k_{x}\) o\(k_{y}\). Estos son de orden\(k \sin \theta\), donde\(\theta\) está el ángulo entre el haz de referencia y la señal. Pero la distancia entre máximos vecinos en la placa fotográfica es, por lo tanto, de orden\[\frac{2 \pi}{k \sin \theta}=\frac{\lambda}{\sin \theta}\]

donde\(\lambda\) está la longitud de onda de la luz. Ya que\(\lambda\) es una distancia muy pequeña, vale la pena escoger\(\theta\) pequeña para extender el patrón en la placa fotográfica.

Tenga en cuenta, también, que los\(C^{2}\) términos del pedido que dejamos caer realmente no hacen ningún daño aunque\(C\) no sean pequeños. Debido a que su\(x\) y\(y\) dependencia es proporcional a la de la señal por su complejo conjugado, lo típico\(k_{x}\) y\(k_{y}\) para estos términos es cero y viajan aproximadamente en la dirección del haz de referencia. No llegan a tu ojo en (13.33).