1.1: Tres modelos de espacio-tiempo

Objetivos de aprendizaje

• Discutir los tres modelos del espacio-tiempo
• El espacio-tiempo aristotélico
• Espacio-tiempo galileo
• El espacio-tiempo de Einstein

“La prueba de una inteligencia de primer nivel es la capacidad de tener en mente dos ideas opuestas al mismo tiempo y aún así conservar la capacidad de funcionar. ” —F. Scott Fitzgerald

El tiempo y el espacio juntos hacen del espacio-tiempo\(\PageIndex{1}\), Figura, el escenario en el que se juega la física. Hasta 1905, los físicos fueron entrenados para aceptar dos teorías mutuamente contradictorias del espacio-tiempo. Voy a llamar a estos los puntos de vista aristotélicos y galileos, aunque mis colegas de esa época se habrían ofendido al ser acusados incluso de aristotelismo parcial.

Figura\(\PageIndex{1}\): 1. Un gráfico típico del movimiento de una partícula: una oscilación. 2. En relatividad, es costumbre intercambiar los ejes, y 3. incluso podemos quitar los ejes por completo.

Espacio-tiempo aristotélico

La figura\(\PageIndex{2}\) muestra un observador y dos relojes, representados usando las convenciones gráficas de la figura\(\PageIndex{1}\) (3). La existencia de tal objeto material en un lugar y tiempo determinados constituye un acontecimiento, que idealizamos como punto, Figura\(\PageIndex{2}\) (2). El espacio-tiempo consiste en el conjunto de todos los eventos. A medida que pasa el tiempo, un objeto físico traza una curva continua, un conjunto de eventos conocidos en el lenguaje relativista como su línea del mundo. Dado que las pantallas de papel y computadora son bidimensionales, los dibujos solo representan una dimensión del espacio más una dimensión del tiempo, que en la relatividad llamamos “\(1+1\)dimensiones”. El universo real tiene tres dimensiones espaciales, por lo que el espacio-tiempo real tiene\(3+1\) dimensiones. La mayor parte, pero no todos, de los fenómenos interesantes en la relatividad especial se pueden entender en\(1+1\) dimensiones, por lo que siempre que sea posible en este libro dibujaré figuras\(1+1\) -dimensionales sin disculpas ni explicaciones.

Figura\(\PageIndex{2}\): 1. Un observador y dos relojes.2. La idealización como eventos. 3. Vectores utilizados para representar las relaciones entre eventos.

La actitud del relativista es que los eventos y las relaciones entre eventos son primarios, mientras que las coordenadas como\(x\) y\(t\) son secundarias y posiblemente irrelevantes. Coordenadas vamos a adjuntar etiquetas como (\(x,t\)) a los puntos, pero esto es como Dios pidiéndole a Adán que nombre a todos los pájaros y animales: a los animales no les importaban los nombres. La Figura\(\PageIndex{2}\) (3) muestra el uso de vectores para indicar relaciones entre puntos. Vector\(o\) es un observador-vector, que conecta dos puntos en la línea mundial de la persona. Señala desde el pasado hacia el futuro. El vector s que conecta los dos relojes es un vector de simultaneidad. Los relojes se han sincronizado previamente uno al lado del otro, y si asumimos que transportarlos a ubicaciones separadas no los interrumpe, entonces el hecho de que ambos relojes lean dos minutos después de las tres nos dice que los dos eventos ocurren al mismo tiempo.

El modelo aristotélico del espacio-tiempo se caracteriza por un conjunto de reglas sobre qué vectores son vectores válidos de observador y simultaneidad. Requerimos que cada\(o\) vector sea paralelo entre sí, e igualmente para\(s\) vectores. Pero, como es habitual con los vectores, permitimos que la flecha se dibuje en cualquier lugar sin considerar que las diferentes ubicaciones tengan ningún significado; es decir, nuestro modelo de espacio-tiempo no permite que diferentes regiones tengan diferentes propiedades.

Figura\(\PageIndex{3}\): Vectores válidos que representan observadores y simultaneidad, según el modelo aristotélico del espacio-tiempo.

Cuando Einstein era estudiante universitario, estas reglas (enunciadas de manera diferente) eran las que le enseñaron a usar para describir la electricidad y el magnetismo. Más tarde recordó imaginarse a sí mismo en una motocicleta, andar junto a una ola de luz e intentar imaginar cómo sus observaciones podrían conciliarse con las ecuaciones de Maxwell. No sé si alguna vez fue lo suficientemente valiente como para describir este sueño a sus profesores, pero si lo hubiera hecho, su respuesta habría sido esencialmente que su hipotético\(o\) vector era ilegal. Se pensó que los buenos\(o\) vectores eran los que representaban a un observador en reposo relativo al éter, un hipotético medio omnipresente cuyas vibraciones eran ondas electromagnéticas. Por tonto que esto nos pudiera parecer cien años después, de hecho fue fuertemente respaldado por las pruebas. Un gran número de experimentos habían verificado la validez de las ecuaciones de Maxwell, y se sabía que si las ecuaciones de Maxwell fueran válidas en coordenadas (\(x,t\)) definidas por un observador\(o\), pasarían a ser inválidas bajo la transformación\((x', t') = (x + vt, t)\) a coordenadas definidas por un observador\(o'\) en movimiento a velocidad\(v\) relativa a\(o\).

Espacio-tiempo galileo

Pero ya se sabía que el modelo aristotélico estaba equivocado cuando se aplicaba a objetos materiales. La clásica demostración empírica de este hecho se produjo alrededor de 1610 con el descubrimiento de Galileo de cuatro lunas orbitando Júpiter, Figura\(\PageIndex{4}\). El aristotelismo en su forma antigua se ideó originalmente como una explicación de por qué los objetos siempre parecían establecerse en un estado natural de reposo según un observador parado en la superficie terrestre. Pero mientras Júpiter volaba a través de los cielos, sus lunas dieron vueltas alrededor de él, sin mostrar ninguna tendencia natural a caer detrás de él como un vaso de papel tirado por la ventana de un automóvil. Así como un observador\(o_1\) parado en la tierra consideraría que la tierra estaba en reposo,\(o_2\) flotando en un globo en las cimas de las nubes de Júpiter diría que las nubes jovianas representaban un estado de reposo igualmente “natural”.

Figura\(\PageIndex{4}\): Simulación de cómo Júpiter y sus lunas podrían aparecer a intervalos de tres horas a través de un telescopio. Debido a que vemos las órbitas circulares de las luna bordeando, sus líneas mundiales aparecen sinusoidales. Durante este periodo de tiempo, la luna más interna\(Io\),, completa medio ciclo.

Nos llevan así a un conjunto diferente, galileo, de reglas para\(o\) y\(s\) vectores. Todos los\(s\) vectores son paralelos entre sí, pero cualquier vector no\(t\) es paralelo a un\(s\) vector es un\(o\) vector válido. (Es posible que deseemos exigir que apunte hacia el futuro en lugar del pasado, pero las leyes de Newton son simétricas bajo la inversión del tiempo, por lo que esto no es estrictamente necesario).

Figura\(\PageIndex{5}\): Vectores válidos que representan observadores y simultaneidad, según el modelo galileano de espacio-tiempo.

El espacio-tiempo galileo, a diferencia del espacio-tiempo aristotélico, no tiene una noción universal de “mismo lugar”. Puedo conducir hasta Gettysburg, Pensilvania, y pararme frente a la placa de bronce que marca el sitio de la trascendental batalla de la Guerra Civil. Pero ¿realmente estoy en el mismo lugar? Un observador en otro planeta diría que nuestro planeta se había movido por el espacio desde 1863.

Paralelismo

Nótese que nuestra descripción geométrica incluye una noción de paralelismo, pero no de medida angular. No sabemos ni nos importa si el “ángulo” entre un\(s\) y un\(o\) es\(90\) grados. Uno representa una distancia, mientras que el otro representa un intervalo de tiempo, y no podemos definir el ángulo entre una distancia y un tiempo. Lo mismo sucedió en el modelo aristotélico; los vectores en Fgure\(\PageIndex{3}\) se dibujaron perpendiculares entre sí simplemente como cuestión de convención, pero se pudo haber utilizado cualquier otro ángulo.

La paradoja de los gemelos galileos

Alice y Betty son gemelas idénticas. Betty realiza un viaje espacial, viajando lejos de la tierra a lo largo del vector\(o_1\) para luego darse la vuelta y volver a encenderse\(o_2\). En tanto, Alice se queda en la tierra. Debido a que se trata de un experimento que involucra objetos materiales, y las condiciones son similares a aquellas bajo las cuales la relatividad galileana ha sido verificada repetidamente por experimento, esperamos que los resultados sean consistentes con la afirmación de la relatividad galilea de que el movimiento es relativo. Por lo tanto parece que debería ser igualmente válido considerar a Betty y a la nave espacial como que habían estado en reposo todo el tiempo, mientras que Alicia y el planeta tierra viajaron alejándose de la nave espacial a lo largo\(o_3\) y luego regresaron vía\(o_4\). Pero esto no es consistente con los resultados experimentales, que muestran que Betty sufre una aceleración violenta en su punto de respuesta, mientras que Alice y los demás habitantes de la tierra no sienten tal efecto.

Figura\(\PageIndex{6}\): Paradoja Gemela.

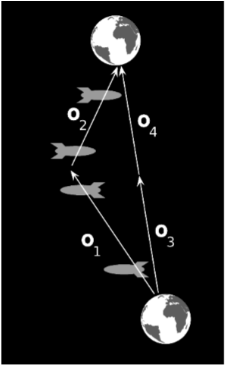
La paradoja se resuelve al darse cuenta de que la relatividad galilea define inequívocamente si dos vectores son paralelos o no. Es cierto que podríamos fijar un marco de referencia en el que\(o_1\) representara la nave espacial permaneciendo en reposo, pero no\(o_2\) sea paralela a\(o_1\), así que en este marco todavía tenemos una buena explicación de por qué Betty siente una aceleración: ha pasado de estar en reposo a estar en movimiento. Independientemente del marco de referencia que escojamos, e independientemente de si incluso fijamos un marco de referencia,\(o_3\) y\(o_4\) somos paralelos entre sí, y esto explica por qué Alice no siente ningún efecto.

El espacio-tiempo de Einstein

Tenemos dos modelos de espacio-tiempo, ninguno de los cuales es capaz de describir todos los fenómenos que observamos. Debido al estado relativamente crudo de la tecnología ca. 1900, requirió una visión considerable para que Einstein reuniera un cuerpo fragmentario de evidencia indirecta y llegara a un modelo consistente y correcto del espacio-tiempo. Hoy, la evidencia es parte de la vida cotidiana. Por ejemplo, cada vez que usas un receptor GPS, estás usando la teoría de la relatividad de Einstein. En algún lugar entre 1905 y hoy, la tecnología se volvió lo suficientemente buena como para permitir experimentos conceptualmente simples que los estudiantes de principios de\(20^{th}\) siglo solo pudieron discutir en términos como “Imagina que podríamos... ”

Figura\(\PageIndex{7}\): El reloj ocupaba dos asientos, y se compraron dos boletos para él bajo el nombre de “Mr. Clock”.

Un buen punto de partida es 1971. En ese año, J.C. Hafele y R.E. Keating llevaron relojes atómicos a bordo de aviones comerciales, Fgure\(\PageIndex{7}\), y dieron la vuelta al mundo, una vez de este a oeste y otra de oeste a este. Hafele y Keating observaron que había una discrepancia entre los tiempos medidos por los relojes de viaje y los tiempos medidos por relojes similares que se quedaron en casa en el Observatorio Naval de Estados Unidos en Washington. El reloj de dirección este perdió tiempo, terminando en\(-59 \pm 10\) nanosegundos, mientras que el que va al oeste ganó\(273 \pm 7\) ns.

Estamos acostumbrados a pensar en el tiempo como absoluto y universal, por lo que es inquietante encontrar que puede volar a diferentes ritmos para diferentes observadores. Sin embargo, los efectos que Hafele y Keating observaron fueron pequeños. Esto tiene sentido: la relatividad galileana ya había sido verificada a fondo para objetos materiales como relojes, planetas y aviones, por lo que una nueva teoría como la de Einstein tuvo que estar de acuerdo con la de Galileo en una buena aproximación, dentro del ámbito de aplicabilidad de la teoría galileana. Este requisito de compatibilidad hacia atrás se conoce como el principio de correspondencia.

Figura\(\PageIndex{8}\): Los tres relojes se mueven hacia el este. A pesar de que el avión que va al oeste se mueve hacia el oeste en relación con el aire, el aire se mueve hacia el este debido a la rotación de la tierra.

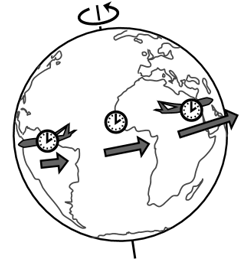
También es tranquilizador que los efectos en el tiempo fueron pequeños en comparación con las duraciones de tres días de los viajes en avión. Por lo tanto, no había oportunidad de escenarios paradójicos como aquel en el que el experimentador que iba al este llegó de nuevo a Washington antes de irse y luego se convenció de no realizar el viaje. Se dice que una teoría que mantiene este tipo de relación ordenada entre causa y efecto satisface la causalidad.

Hafele y Keating estaban probando predicciones cuantitativas específicas de relatividad, y las verificaron dentro de las barras de error de su experimento. Trabajemos hacia atrás e inspeccionemos los resultados empíricos en busca de pistas sobre cómo funciona el tiempo. Los desacuerdos entre los relojes sugieren que la simultaneidad no es absoluta: diferentes observadores tienen diferentes nociones de simultaneidad, como se sugiere en la Figura\(\PageIndex{9}\). Así como la relatividad galileana liberó a los\(o\) vectores de la restricción de ser paralelos entre sí, Einstein libera a los\(s\) vectores. Galileo convirtió “mismo lugar” en un concepto ambiguo, mientras que Einstein hizo lo mismo con “simultáneo”. Pero debido a que un observador en particular sí tiene métodos de sincronización de relojes (por ejemplo, sincronización de Einstein, ejemplo\(\PageIndex{4}\)), la definición de simultaneidad no es completamente arbitraria. Para cada\(o\) vector tenemos un\(s\) vector correspondiente, que representa la opinión de ese observador en cuanto a lo que constituye simultaneidad. Debido a que la convención sobre una\(x - t\) gráfica cartesiana es dibujar los ejes en ángulo recto entre sí, nos referimos a tal par de vectores como ortogonales, pero la palabra no debe interpretarse literalmente, ya que no podemos definir un ángulo real entre un intervalo de tiempo y un desplazamiento espacial.

Figura\(\PageIndex{9}\): Según Einstein, la simultaneidad es relativa, no absoluta.

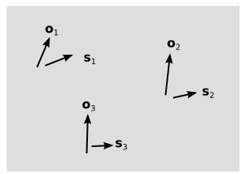
¿Cuáles son entonces las reglas para la ortogonalidad? La figura\(\PageIndex{10}\) muestra tres posibilidades. En cada caso, tenemos un par inicial de vectores\(o_1\) y\(s_1\) que suponemos son ortogonales, y luego dibujamos un nuevo par\(o_2\) y\(s_2\) para un segundo observador que está en movimiento relativo al primero. Ya se ha descartado el caso galileo\(s_1\), donde\(s_2\) permanece paralelo a,. El segundo caso es aquel en el que\(s\) gira en la misma dirección que\(o\). Esta está prohibida por la causalidad, porque si seguimos rotando, eventualmente podríamos terminar rotando\(o\) por\(180\) grados, así por un proceso continuo de aceleración, podríamos enviar a un observador a un estado en el que se invirtiera su sentido del tiempo. Nos queda una sola posibilidad para el espacio-tiempo de Einstein, que es aquella en la que una rotación en sentido horario de\(o\) provoca una rotación en sentido antihorario de\(s\), como cerrar un par de tijeras.

Figura\(\PageIndex{10}\): Posibilidades para el comportamiento de la ortogonalidad.

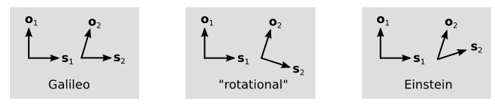
Ahora hay un límite a lo lejos que puede llegar este proceso, o de lo contrario el\(s\) y eventualmente\(o\) estaría en la misma línea. Pero esto es imposible, pues un\(s\) vector válido nunca puede ser válido\(o\), ni\(o\) un válido\(s\). Tal posibilidad significaría que un observador describiría dos puntos diferentes en su propia línea mundial como simultáneos, pero un observador para el que no pasa el tiempo no es observador en absoluto, ya que la observación implica recolectar datos y luego poder recordarlos en algún momento posterior. Se concluye que existe una línea diagonal que forma el límite entre el conjunto de\(s\) vectores posibles y el conjunto de\(o\) vectores válidos. Esta línea tiene cierta pendiente, y la inversa de esta pendiente corresponde a cierta velocidad, que aparentemente es una propiedad universal y fija del espacio-tiempo de Einstein. Esta velocidad que llamamos\(c\), y el principio de correspondencia nos dice que\(c\) debe ser muy grande, porque de lo contrario los efectos einsteinianos, o “relativistas”, como la distorsión del tiempo habrían sido grandes incluso para el movimiento a velocidades cotidianas; en el experimento de Hafele-Keating eran bastante pequeños, incluso a la alta velocidad de un jet de pasajeros.

Si bien\(c\) es un número grande cuando se expresa en metros por segundo, para mayor comodidad en la relatividad siempre elegiremos unidades de tal manera que\(c = 1\). El límite entre\(o\) vectores\(s\) y luego aparece en los diagramas de espacio-tiempo como una línea diagonal en\(\pm 45\) grados. En más de una dimensión espacial, este límite forma un cono, Ffigure\(\PageIndex{11}\), y por razones que se harán más claras en un momento, este cono se llama cono de luz. Los vectores que se encuentran dentro del cono de luz se denominan similares al tiempo, a los que están afuera como al espacio y a los del cono mismo como parecidos a la luz o nulos.

Figura\(\PageIndex{11}\): El cono de luz.

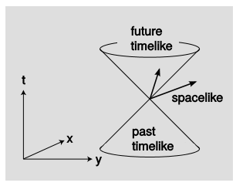
Una ventaja importante de la relatividad de Einstein sobre la de Galileo es que es compatible con la observación empírica de que algunos fenómenos viajan a cierta velocidad fija. La luz viaja a una velocidad fija, al igual que otros fenómenos como las ondas gravitacionales (detectadas por primera vez directamente en 2016). Así lo hacen todas las partículas sin masa (subsección 4.3.4). Esta velocidad fija es\(c\), y todos los observadores están de acuerdo en ello. En 1905, el único fenómeno conocido por viajar\(c\) era la luz, por lo que \(c\)suele describirse como la “velocidad de la luz”, pero desde el punto de vista moderno funciona más como una especie de factor de conversión entre nuestras unidades de medida para el tiempo y el espacio. Es una propiedad del espacio-tiempo, no una propiedad de la luz.

Más fundamentalmente,\(c\) es la velocidad máxima de causa y efecto. Si pudiéramos propagar causa y efecto, por ejemplo, transmitiendo una señal, a una velocidad mayor que\(c\), entonces el siguiente argumento muestra que estaríamos violando ya sea la causalidad o el principio de que el movimiento es relativo. Si una señal pudiera propagarse a una velocidad mayor que\(c\), entonces el vector que \(r\)conecta la causa y el efecto sería espacial. Al abrir y cerrar las “tijeras” de Figura\(\PageIndex{10}\), siempre podemos encontrar un observador\(o\)\(r\) que considere un vector de simultaneidad. Así, si es posible una propagación más rápida que la luz, entonces es posible la propagación instantánea, al menos para algún observador. Dado que la moción es relativa, esto debe ser posible para todos los observadores, independientemente de su estado de movimiento. Por lo tanto, cualquier vector espacial es uno a lo largo del cual podemos enviar una señal. Pero al agregar dos vectores espaciales podemos hacer un vector que yacía en el pasado tiempo como cono de luz, así al retransmitir la señal podríamos enviar un mensaje al pasado, violando la causalidad.

Al interpretar este argumento, tenga en cuenta que ni la relatividad del movimiento ni la causalidad son una necesidad lógica; ambas son solo generalizaciones basadas en un cuerpo de pruebas. Para más información sobre la causalidad, y su estado empírico incierto, ver sección 2.1.

El giroscopio láser de anillo

Si has florecido en un avión a reacción, puedes agradecerle a la relatividad por ayudarte a evitar chocar contra una montaña o un océano. La figura\(\PageIndex{12}\) muestra una pieza estándar de equipo de navegación llamada giroscopio láser anular. Un haz de luz se divide en dos partes, se envía alrededor del perímetro del dispositivo y se reúne. Dado que la velocidad de la luz es constante, esperamos que las dos partes vuelvan a juntarse al mismo tiempo. Si no lo hacen, es evidencia de que el dispositivo ha estado rotando. La computadora del avión detecta esto y anota cuánta rotación se ha acumulado.

Figura\(\PageIndex{12}\): Un giroscopio láser anular.

Sin frecuencia - Dependencia

La relatividad solo tiene una velocidad universal, por lo que requiere que todas las ondas de luz viajen a la misma velocidad, independientemente de su frecuencia y longitud de onda. Actualmente las mejores pruebas experimentales de la invarianza de la velocidad de la luz con respecto a la longitud de onda provienen de observaciones astronómicas de ráfagas de rayos gamma, que son emanaciones repentinas de luz de alta frecuencia, que se cree que se originan a partir de una explosión de supernova en otra galaxia. Una de esas observaciones, en 2009, encontró que los tiempos de llegada de todas las diferentes frecuencias en la ráfaga diferían en no más de\(2\) segundos de un tiempo total en vuelo del orden de ¡diez mil millones de años!

Tren de Einstein

El Fgure\(\PageIndex{13}\) muestra un famoso experimento pensativo ideado por Einstein. Un tren se mueve a velocidad constante hacia la derecha cuando relámpagos golpean el suelo cerca de su parte delantera y trasera. Alice, de pie sobre la tierra en el punto medio de las flashes, observa que la luz de las dos flashes llega simultáneamente, por lo que dice que los dos golpes deben haber ocurrido simultáneamente. Bob, por su parte, está sentado a bordo del tren, en su centro. Pasa junto a Alice en el momento en que luego Alice se da cuenta de que ocurrieron los flashes. Posteriormente, recibe flash\(2\), y luego flash\(1\). Infiere que dado que ambas flashes viajaron la mitad de la longitud del tren, la flash\(2\) debió haber ocurrido primero. ¿Cómo se puede conciliar esto con la creencia de Alice de que los flashes fueron simultáneos?

Figura\(\PageIndex{13}\): Tren de Einstein

La figura\(\PageIndex{14}\) muestra el diagrama espacio-tiempo correspondiente. Parece paradójico que Alice y Bob no estén de acuerdo sobre la simultaneidad, pero esto es sólo porque tenemos un prejuicio arraigado a favor de la relatividad galilea. El método de Alice para determinar que\(1\) y\(2\) eran simultáneos es válido, y se conoce como sincronización de Einstein. La línea discontinua que conecta\(1\) y\(2\) es ortogonal a la línea del mundo de Alice. Pero Bob tiene una opinión diferente sobre lo que constituye simultaneidad. La línea discontinua inclinada es ortogonal a su línea del mundo. Según Bob,\(2\) sucedió antes del tiempo representado por esta línea,\(1\) después.

Figura\(\PageIndex{14}\): Diagrama espacio-tiempo correspondiente

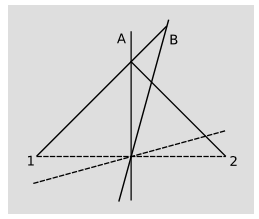
Por supuesto, el ejemplo\(\PageIndex{4}\) es poco práctico como se describe, ya que los trenes reales no viajan a velocidades\(c\) cercanas a la suciedad. Decimos que sus velocidades son “no relativistas”. Debido a que Einstein acuñó el término “relatividad”, y su versión de la relatividad reemplazó a la de Galileo, normalmente se entiende que la palabra no modificada se refiere a la relatividad einsteiniana. Un físico que estudia la relatividad de Einstein es relativista. Un objeto material que se mueve a una velocidad muy cercana\(c\) se describe como ultrarelativista. A menudo se escucha a laicos describir la relatividad en términos de ciertos efectos que sucederían “si fueras a la velocidad de la luz. ” De hecho, como veremos en el capítulo 3 y capítulo 4, no es posible acelerar los objetos materiales a\(c\), y en todo caso eso no es necesario. Los efectos relativistas existen a todas las velocidades, pero son débiles a velocidades pequeñas en comparación con\(c\).

Valor numérico de c

En este libro utilizaremos unidades en las que\(c = 1\). Sin embargo, muchos principiantes están molestos por la pregunta de por qué\(c\) tiene el valor particular que tiene en un sistema dado de unidades como el SI. Relacionado con esto está la cuestión de si alguna vez\(c\) podría cambiar, de modo que medirlo hoy y medirlo mañana daría resultados ligeramente diferentes. En un sistema de unidades donde\(c\) tiene unidades, su valor es lo que es sólo por nuestra elección de unidades, y no hay manera significativa de probar si cambia.

Tomemos el SI como ejemplo de un sistema de unidades. El SI se configuró originalmente para que el medidor y el segundo se definieran en términos de propiedades de nuestro planeta. El medidor era una cuarenta millonésima parte de la circunferencia de la tierra, y el segundo era\(1/86,400\) de un día solar medio. Así, cuando expresamos\(c\) como\(3.0 \times 10^8 m/s\), básicamente estamos especificando el factor por el cual\(c\) excede la velocidad a la que un punto en el ecuador va alrededor del centro de la tierra (con factores de conversión adicionales de\(40,000,000\) y\(86,400\) arrojados). Dado que las propiedades de nuestro planeta son accidentes de la formación del sistema solar, no existe una teoría física que nos pueda decir por qué\(c\) tiene este valor en la versión original francés-revolucionaria de la SI.

Las unidades base del SI fueron redefinidas a lo largo de los siglos. Hoy en día, el segundo se define en términos de un estándar atómico, y el medidor se define como\(1/299,792,458\) de un segundo de luz. Por lo tanto \(c\)tiene un valor definido de exactamente\(299,792,458 m/s\). Nuevamente, encontramos que el valor numérico de no\(c\) tiene significación fundamental; es meramente una cuestión de definición. Es posible formar la relación sin unidades\(\alpha = e^2/\tilde{h} c \approx 1/137\), llamada constante de estructura fina. Su valor no depende de nuestra elección de unidades, por lo que es posible hacer experimentos para buscar cambios en su valor a lo largo del tiempo, por ejemplo, comparando el espectro de hidrógeno en la tierra con el espectro de estrellas distantes, cuya luz ha tardado miles de millones de años en llegar a nosotros. Incluso se han hecho afirmaciones en el sentido de que estas observaciones sí muestran un cambio, aunque esto parece haber sido un error. Si tal cambio ocurriera, no podríamos atribuirlo inequívocamente a un cambio en\(c\) más que a un cambio en\(\tilde{h}\) o a la carga fundamental. Los estándares utilizados para definir nuestras unidades podrían cambiar con el tiempo. Se sospecha que el estándar de platino-iridio para el kilogramo en París perdió alrededor de\(50\) µg de masa durante el siglo pasado. Incluso el estándar atómico utilizado para definir el segundo podría estar cambiando debido a la física más allá de nuestro conocimiento actual. Un cambio en\(c\) podría producir tal cambio, pero cualquier cambio de este tipo también podría ser producido por cambios en otras constantes físicas, como las otras que ocurren en la constante de estructura fina. Dichos temas se discuten con mayor profundidad en la Sección 9.6.

Pregunta de discusión\(\PageIndex{1}\)

El ametrallador en el Fgure\(\PageIndex{15}\) envía un chorro de balas. Supongamos que las balas están siendo disparadas al espacio exterior, y que las distancias recorridas son de billones de millas (para que la figura humana en el diagrama no esté a escala). Después de mucho tiempo, las balas llegan a los puntos mostrados con puntos que están todos igualmente lejos del arma. Sus llegadas a esos puntos son eventos\(A\) a través\(E\), que ocurren en diferentes momentos. La cadena de impactos se extiende a través del espacio a una velocidad mayor que\(c\). ¿Esto viola la relatividad especial?

Figura\(\PageIndex{15}\): Ametralladora rociando balas