3.3: Combinación de Velocidades

Objetivos de aprendizaje

• Explicar cómo agregar velocidades relativisticamente

En la física no relativista, las velocidades se suman en movimiento relativo. Por ejemplo, si una embarcación se mueve en relación con un río, y el río se mueve en relación con la tierra, entonces la velocidad de la embarcación en relación con la tierra se encuentra por adición vectorial. Este comportamiento lineal no puede sostenerse relativisticamente. Por ejemplo, si una nave espacial se mueve con relación a la tierra a velocidad$3/5$ (en unidades con$c = 1$), y lanza una sonda a velocidad$3/5$ relativa a sí misma, no podemos tener la sonda moviéndose a una velocidad$6/5$ relativa a la tierra, porque esto sería mayor que el máximo velocidad de causa y efecto, que es$1$. Para ver cómo sumar velocidades relativisticamente, consideramos el efecto de llevar las dos transformaciones de Lorentz una tras otra, figura$\PageIndex{1}$.

Figura$\PageIndex{1}$: Dos transformaciones de Lorentz$v = 3/5$ se aplican una tras otra. Las transformaciones se representan de acuerdo con las convenciones gráficas de la sección 1.4.

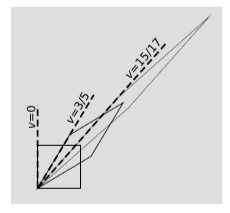
La pendiente inversa del lado izquierdo de cada paralelogramo indica su velocidad relativa al marco original, representado por el cuadrado. Dado que el lado izquierdo del paralelogramo final no ha barrido más allá de la diagonal, claramente representa una velocidad de menos de$1$, no más. Para determinar el resultado, utilizamos el hecho de que los$D$ factores se multiplican. Elegimos velocidades$3/5$ porque da$D = 2$, lo que es fácil de trabajar. Duplicar la diagonal larga dos veces da un factor de estiramiento general de$4$, y resolver la ecuación$D(v) = 4$ para$v$ da el resultado,$v = 15/17$.

Ya podemos ver la respuesta a la pregunta 2 en la sección 3.0: Preludio a la Cinemática. Si seguimos acelerando una nave espacial de manera constante, simplemente estamos continuando el proceso de aceleración que se muestra en la figura$\PageIndex{1}$. Si hacemos esto indefinidamente, la velocidad se acercará$c = 1$ pero nunca la superará. (Para más información sobre este tema de ir más rápido que la luz, ver sección 4.7.)

Ejemplo$\PageIndex{1}$: Accelerating electrons

Figura$\PageIndex{2}$: Aceleración de electrones

La figura$\PageIndex{2}$ muestra los resultados de un experimento de 1964 de Bertozzi en el que los electrones fueron acelerados por el campo eléctrico estático$E$ de un acelerador Van de Graaff de longitud$l_1$. Entonces se les permitió volar por una línea de haz de longitud$l_2 = 8.4$$m$ sin que se les actúe por ninguna fuerza. El tiempo de vuelo$t_2$ se utilizó para encontrar la velocidad final$v = \frac{l_2}{t_2}$ a la que habían sido acelerados. (Para que la porción de baja energía de la gráfica sea legible, se omite el punto de datos de mayor energía de Bertozzi).

Si creyéramos en las leyes de Newton, entonces los electrones tendrían una aceleración

$$a_N = Ee/m$$

lo que sería constante si, como pretendemos por el momento, el campo$E$ fuera constante. (El campo eléctrico dentro de un acelerador de Van de Graaff no es realmente del todo uniforme, pero esto va a resultar no importar). La predicción newtoniana para el tiempo durante el cual se produce esta aceleración es

$$t_N = \sqrt{2ml_1/eE}$$

Una aceleración$a_N$ que actúa por un tiempo$t_N$ debe producir una velocidad final

$$a_Nt_N = \sqrt{2eV/m}$$

donde$V = El_1$ esta la diferencia de voltaje. (Por conservación de energía, esta ecuación se mantiene aunque el campo no sea constante). La línea continua en la gráfica muestra la predicción de las leyes de Newton, que es que una fuerza constante ejercida de manera constante a lo largo del tiempo producirá una velocidad que se eleva linealmente y sin límite.

Los datos experimentales, mostrados como puntos negros, cuentan claramente una historia diferente. La velocidad asintóticamente se acerca a un límite, que identificamos como$c$. La línea discontinua muestra las predicciones de la relatividad especial, que aún no estamos listos para calcular porque aún no hemos visto cómo la energía cinética depende de la velocidad a velocidades relativistas.

Obsérvese que la relación entre el primer y segundo fotogramas de referencia en la figura$\PageIndex{1}$ es la misma que la relación entre el segundo y el tercero. Por lo tanto, si un pasajero va a sentir una sensación constante de aceleración (o, de manera equivalente, si un acelerómetro a bordo del barco va a mostrar una lectura constante), entonces el tiempo adecuado requerido para pasar del primer cuadro al segundo debe ser el mismo que el tiempo adecuado para pasar del segundo al tercero. Una buena manera de expresar esto es definir la rapidez\( η =\ ln D\). Combinar velocidades significa multiplicar$D$, lo que es lo mismo que sumar sus logaritmos. Por lo tanto podemos escribir la regla relativista para combinar velocidades simplemente como

$$_ηc = η_1 + η_2$$

Los pasajeros perciben la aceleración como constante si$η$ aumentan en la misma cantidad por unidad de tiempo adecuado. En otras palabras, podemos definir una aceleración adecuada$dη/dτ$, que corresponde a lo que mide un acelerómetro.

La rapidez es conveniente y útil, y se utiliza con mucha frecuencia en la física de partículas. Pero en términos de velocidades ordinarias, la regla para combinar velocidades también se puede reescribir usando esta identidad de la sección 3.6 como

$$v_c = \dfrac{v_1+v_2}{1+v_1v_2}. \label{eq3}$$

Ejercicio$\PageIndex{1}$

¿Cómo podemos decir que la Ecuación\ ref {eq3} está escrita en unidades naturales? Reescribirlo en unidades SI.