3.E: Cinemática (Ejercicios)

Q1

Fred compra un boleto en una nave espacial que acelerará a una velocidad ultrarelativista$v$ tal que$c - v$ es sólo$6\: m/s$. Fred estaba en el equipo de pista en la secundaria, así que sabe que puede correr por ahí$8\: m/s$. Una vez que el barco esté al día, Fred planea correr en dirección hacia adelante, convirtiéndose así en el primer humano en superar la velocidad de la luz. Aparte de la posible falta de gravedad para permitir correr, ¿qué tiene de malo el plan de Fred?

Q2

1. En la ecuación$v_c = \tfrac{v_1 +v_2}{1+v_1v_2}$ para combinación de velocidades, interprete el caso donde una de las velocidades (pero no la otra) es igual a la velocidad de la luz.
2. Interpretar el caso donde el denominador va a cero.
3. Usa la serie geométrica para reescribir el factor\ [(tfrac {1} {1+v_1v_2}\), y luego expandir la expresión para$v_c$ como serie en$v_1$ y$v_2$, conservando términos hasta tercer orden en velocidad. ¿Cómo se relaciona esto con el principio de correspondencia?

Q3

Determinar cuáles de las identidades de la sección 3.6 necesitan ser modificadas para ser válidas en unidades con$c \neq 1$, y describir cómo deben ser modificadas.

Q4

El Gran Colisionador de Hadrones acelera los rayos contrarrotantes de protones y los choca de frente. La energía del haz se ha incrementado gradualmente, y el acelerador está diseñado para alcanzar una energía máxima de$14\: TeV$, correspondiente a una rapidez de$10.3$.

1. Encuentra la velocidad del haz.
2. En cualquier colisión, la energía cinética disponible para hacer algo inelástico (destrozar tu auto, producir reacciones nucleares,...) es la energía en el marco del centro de masa; en cualquier otro marco, hay energía cinética inicial que también debe estar presente en el estado final debido a la conservación del impulso. Supongamos que un protón particular en el haz LHC nunca sufre una colisión con un protón del haz opuesto, y en su lugar se desperdicia al ser vertido en un tope de haz. Digamos que esta colisión es con un protón en un átomo de hidrógeno dejado atrás por la huella dactilar de alguien. Encuentra las velocidades de los dos protones en su marco común de centro de masa.

Q5

Cada satélite GPS se encuentra en una órbita con un radio de$26,600\: km$, con un periodo orbital de medio día sideral, dándole una velocidad de$3.88\: km/s$. Se sintoniza el reloj atómico a bordo de dicho satélite$10.22999999543\: MHz$, el cual se elige de manera que cuando el satélite está directamente sobre la cabeza, el efecto de la dilatación del tiempo (desplazamiento Doppler transversal), combinado con un efecto general-relativista debido a la gravedad, resulte en una frecuencia de exactamente$10.23\: MHz$. (El GPS comenzó como un proyecto militar, y cuenta la leyenda que los altos mandos, sospechosos de las locas cosas de la relatividad, exigieron que los satélites estuvieran equipados con un interruptor de software para apagar la corrección, por si acaso los físicos se equivocaran). Hay oscilaciones superpuestas sobre estos efectos estáticos debido a los desplazamientos Doppler longitudinales a medida que los satélites se acercan y retroceden de un observador dado en el suelo.

1. Calcular la frecuencia máxima desplazada por Doppler para un hipotético observador en el espacio exterior al que está siendo abordado directamente por el satélite en su órbita.
2. En realidad, el mayor componente longitudinal posible de la velocidad es considerablemente menor que esto debido a la geometría. Usa el tamaño de la tierra para determinar esta velocidad y la frecuencia máxima correspondiente.

Q6

Verificar directamente, utilizando la geometría de la figura a continuación, que para$v = 3/5$, el factor de desplazamiento Doppler es$D = 2$. (No se limite$v = 3/5$ a enchufar a la fórmula$D =\sqrt{\frac{1 + v}{1-v}}$.)

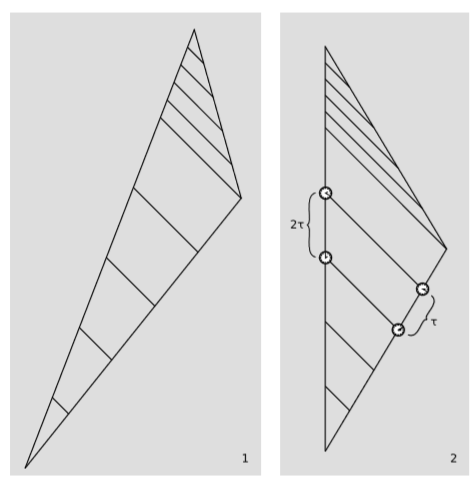
Q7

Generalizar el cálculo numérico del problema Q6 para probar el resultado general$D =\sqrt{\frac{1 + v}{1-v}}$.

Q8

Expandir la ecuación relativista para el desplazamiento Doppler longitudinal de la luz$D(v)$ en una serie de Taylor, y encontrar los dos primeros términos que no se desvanecen. Demostrar que estos dos términos concuerdan con la expresión no relativista, por lo que cualquier efecto relativista es de orden superior en$v$.

Q9

Demostrar, como se afirma en la sección 3.5, que debemos tener$a \cdot v = 0$ para que la velocidad de cuatro vectores se mantenga normalizada correctamente.

Q10

En el Ejemplo 3.5.1 se describe el movimiento de un objeto que tiene una aceleración adecuada constante$a$, siendo la línea mundial$t = \frac{1}{a} \sinh a\tau$ y$x = \frac{1}{a} \cosh a\tau$ en las coordenadas Minkowski de un observador particular.

1. Demostrar los siguientes resultados para$γ$ y para la (tres) velocidad y (tres) aceleración medidas por este observador. $$\gamma =\cosh a\tau \\ v = \tanh a\tau \\ \text{acceleration} = a\cosh ^{-3}a\tau$$ Hacer los cálculos simplemente tomando la primera y segunda derivadas de posición con respecto al tiempo. Encontrará útiles los siguientes datos: $$1-\tanh ^2 = \cosh ^{-2}\\ \frac{\mathrm{d} }{\mathrm{d} x} \tanh = \cosh ^{-2}x$$
2. Interpretar los resultados en el límite de grandes$τ$.

Q11

En el Ejemplo 3.5.1 se describe el movimiento de un objeto que tiene una aceleración adecuada constante$a$, siendo la línea mundial$t = \frac{1}{a} \sinh a\tau$ y$x = \frac{1}{a} \cosh a\tau$ en las coordenadas Minkowski de un observador particular. Encuentra los cuatro vectores de velocidad y aceleración correspondientes.

Q12

Partiendo de los resultados del problema Q11, repetir el problema Q10a utilizando las técnicas de la sección 3.7. Te resultará útil saberlo$1-\tanh ^2 = \cosh ^{-2}$.

Q13

Let$v$ Ser un vector de velocidad dirigido al futuro, correctamente normalizado. Comparar el valor de$v\cdot v$ en la$+---$ firma utilizada en este libro con su valor en la firma$-+ ++$.

Q14

1. Demostrar la relación$\frac{\mathrm{d} \gamma }{\mathrm{d} t} = \gamma ^3 a_o\cdot v_o$, en el caso especial donde el movimiento es lineal.
2. Generalizar el resultado a$3 + 1$ dimensiones.

Q15

Derivar la identidad$a_o = \frac{1}{(o\cdot v)^2}\left [ P_o a - (o\cdot a)v_a \right ]$.

Q16

Recapitulando la geometría en la figura siguiente, deja$W$ ser una línea de mundo suave, similar al tiempo,$E$ un evento no encendido$W$, y$r$ el vector de$E$ a un punto en$W$, parametrizado por el tiempo adecuado$τ$. Definir la distancia adecuada$l$ entre$E$ y un punto on$W$ as$l^2 = -(P_v r)^2$, donde el cuadrado indica un producto interno del vector consigo mismo, y el signo menos es porque usamos la$+---$ firma. Demostrar eso$\frac{\mathrm{d} l^2}{\mathrm{d} \tau } = 2(r\cdot v)(r\cdot a)(v\cdot v)$, donde el factor final es sólo un signo dependiente de la firma. ¿Tiene sentido esto cuando$W$ es inercial? Dé un ejemplo donde la derivada se desvanece porque el primer factor es cero, y otro ejemplo donde el segundo factor es el que desaparece (pero$a \neq 0$).

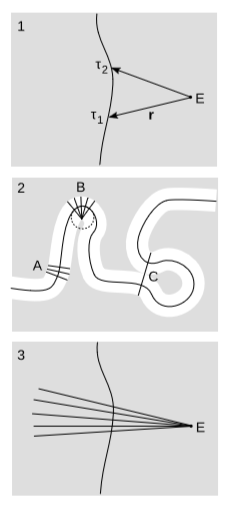
Q17

Considera que un observador$O$ se mueve a lo largo de una línea mundial$W$ con el movimiento de aceleración constante definido en el Ejemplo 3.5.1. En la sección 3.9, dimos las coordenadas de un determinado suceso$E$ que nunca fue “ahora” como lo describió nuestro observador. El propósito de este problema es analizar que esta es una forma más elegante y coordinada-invariante. $P$Sea un punto sobre$W$, que$B$ sea el evento descrito en la sección 3.9, y dejar$x = \overrightarrow{BP}$,$h = \overrightarrow{BE}$, y$r = \overrightarrow{EP}$.

1. Demostrar que$W$, que originalmente se describió en un cierto conjunto de coordenadas, puede en su lugar por definido por el hecho de que$x\cdot v = 0$ para cada punto en$W$.
2. Demuestre que si$h$ es timelike, entonces nunca$r\cdot v$ es cero.