8.1: Fuentes en la Relatividad General (Parte 1)

Fuentes puntuales en una teoría independiente del fondo

La ecuación de Schrödinger y las ecuaciones de Maxwell tratan al espacio-tiempo como una etapa en la que las partículas y los campos representan sus roles. La relatividad general, sin embargo, es esencialmente una teoría del espacio-tiempo mismo. El papel que desempeñan los átomos o los rayos de luz es tan periférico que para cuando Einstein había derivado una versión aproximada de la métrica Schwarzschild, y la utilizó para encontrar la precesión del perihelio de Mercurio, todavía solo tenía ideas vagas de cómo encajarían la luz y la materia en el cuadro. En su cálculo, Mercurio desempeñó el papel de una partícula de prueba: un bulto de masa tan pequeño que puede ser arrojado al espacio-tiempo para medir la curvatura del espacio-tiempo, sin preocuparse por su efecto sobre el espacio-tiempo, que se supone que es insignificante. De igual manera el sol fue tratado como en una de esas piezas orquestales en las que algunos de los metales tocan desde fuera del escenario, para producir el efecto de una segunda banda escuchada desde la distancia. Su masa aparece simplemente como un parámetro ajustable m en la métrica, y si nunca hubiéramos oído hablar de la teoría newtoniana no habríamos tenido forma de saber interpretar m.

Cuando Schwarzschild publicó su solución exacta a las ecuaciones de campo vacío, Einstein sufría de indigestión filosófica. Su fuerte creencia en el principio de Mach le llevó a creer que había una paradoja implícita en un espacio-tiempo exacto con solo una masa en él. Si las ecuaciones de campo de Einstein significaran algo, creía que tenían que ser interpretadas en términos del movimiento de un cuerpo relativo a otro. En un universo con una sola partícula masiva, no habría movimiento relativo, y así, le pareció, ningún movimiento de ningún tipo, y ninguna interpretación significativa para el espacio-tiempo circundante.

No sólo eso, sino que la solución de Schwarzschild tenía una singularidad en su centro. Cuando una teoría clásica de campo contiene singularidades, creía Einstein, contiene las semillas de su propia destrucción. Como hemos visto en la sección 6.3, este tema aún está lejos de resolverse, un siglo después.

Por mucho que le hubiera gustado repudiarlo, Einstein estaba ahora en posesión de una solución a sus ecuaciones de campo para una fuente puntual. En una teoría lineal, dependiente del fondo como el electromagnetismo, el conocimiento de tal solución conduce directamente a la capacidad de anotar las ecuaciones de campo con fuentes incluidas. Si la ley de Coulomb nos dice la\(\frac{1}{r^{2}}\) variación del campo eléctrico de una carga puntual, entonces podemos inferir la ley de Gauss. La situación en la relatividad general no es así de sencilla. Las ecuaciones de campo de la relatividad general, a diferencia de la ley del Gauss, son no lineales, por lo que no podemos decir simplemente que un planeta o una estrella es una solución que se encuentra sumando una gran cantidad de soluciones punto-fuente. Tampoco está claro cómo se podría representar una fuente móvil, ya que la singularidad es un punto que ni siquiera forma parte de la estructura continua del espacio-tiempo (y su ubicación también se oculta detrás de un horizonte de eventos, por lo que no se puede observar desde el exterior).

La ecuación de campo de Einstein

El tensor de Einstein

Dadas estas dificultades, no es sorprendente que el primer intento de Einstein de incorporar fuentes a su ecuación de campo fuera un callejón sin salida. Postuló que la ecuación de campo tendría el tensor Ricci en un lado, y el tensor tensión-energía\(T^{ab}\) (Sección 5.2) por el otro,

\[R_{ab} = 8 \pi T_{ab},\]

donde un factor de a la\(\frac{G}{c^{4}}\) derecha es suprimido por nuestra elección de unidades, y el 8\(\pi\) se determina sobre la base de la consistencia con la gravedad newtoniana en el límite de campos débiles y bajas velocidades. El problema con esta versión de las ecuaciones de campo se puede demostrar contando variables. R y T son tensores simétricos, por lo que la ecuación de campo contiene 10 restricciones en la métrica: 4 de los elementos diagonales y 6 de los fuera de diagonal.

Además, la conservación local de la energía masiva requiere la propiedad libre de divergencias\(\nabla_{b}T^{ab} = 0\). Para construir un ejemplo, recordamos que el único componente\(T\) para el que hasta ahora hemos introducido cualquier interpretación física es\(T^{tt}\), que da la densidad de la masa-energía. Supongamos que teníamos un tensor de tensión-energía cuyos componentes eran todos cero, excepto por un componente tiempo-tiempo que variaba como\(T^{tt} = kt\). Esto describiría una región del espacio en la que la masa-energía aparecía o desaparecía uniformemente en todas partes a un ritmo constante. Para prohibir tales ejemplos, necesitamos poseer la propiedad libre de divergencias. Esto es exactamente análogo a la ecuación de continuidad en mecánica de fluidos o electromagnetismo,

\[\dfrac{\partial \rho}{\partial t} + \nabla \cdot \textbf{J} = 0\]

(o\(\nabla_{a} J^{a}\) = 0), que establece que se conserva la cantidad de fluido o carga.

Pero imponer la condición libre de divergencias agrega cuatro restricciones más a la métrica, para un total de 14. La métrica, sin embargo, es un tensor simétrico rank-2 en sí, por lo que solo tiene 10 componentes independientes. Esta sobredeterminación de la métrica sugiere que la ecuación de campo propuesta no permitirá en general que una solución evolucione hacia adelante en el tiempo a partir de un conjunto de condiciones iniciales dadas en una superficie espacial, y esto resulta ser cierto. De hecho, se puede demostrar que las únicas soluciones posibles son aquellas en las que las trazas R = R ^a y\(T = T^a_a\) son constantes _a lo largo del espacio-tiempo.

La solución es reemplazar\(R_{ab}\) en el campo las ecuaciones por un tensor diferente\(G_{ab}\), llamado el tensor de Einstein, definido por

\[G_{ab} = R_{ab} − \left(\dfrac{1}{2}\right)Rg_{ab}\]

o

\[G_{ab} = 8 \pi T_{ab}\]

El tensor Einstein se construye exactamente para que esté libre de divergencias,\(\nabla_{b} G^{ab}\) = 0. (Esto no es obvio, pero se puede probar por cómputo directo.) Por lo tanto, cualquier tensor de energía de estrés que satisfaga la ecuación de campo es automáticamente sin divergencia y, por lo tanto, no es necesario aplicar restricciones adicionales para garantizar la conservación de la energía masiva.

Ejercicio\(\PageIndex{1}\):

Autocomprobación: ¿Reemplazar R _ab por G _ab invalida la métrica Schwarzschild?

Este procedimiento de hacer que la conservación local de la energía masiva se “incorpore” a las ecuaciones de campo es análogo a la forma en que se trata la conservación de la carga en electricidad y magnetismo, donde se desprende de las ecuaciones de Maxwell en lugar de tener que agregarse como una restricción separada.

Interpretación del tensor estres-energía

El tensor estres-energía se introdujo brevemente en la sección 5.2. Al aplicar el límite newtoniano de la ecuación de campo a la métrica Schwarzschild, encontramos que T ^tt debe identificarse como la densidad de masa\(\rho\). La métrica Schwarzschild describe un espacio-tiempo usando coordenadas en las que la masa está en reposo. En las aplicaciones cosmológicas que vamos a considerar en breve, también tiene sentido adoptar un marco de referencia en el que la masa-energía local esté, en promedio, en reposo, por lo que podemos seguir pensando en T ^tt como la densidad de masa (promedio). Por simetría, T debe ser diagonal en dicho marco. Por ejemplo, si tuviéramos T ^tx ≠ 0, entonces la dirección x positiva se distinguiría de la dirección x negativa, pero no hay nada que permita tal distinción.

Ejemplo 1: Polvo en un marco diferente

Como se discutió en el ejemplo 14, es conveniente en cosmología distinguir entre radiación y “polvo”, es decir, materiales no interactuantes y no relativistas como el gas hidrógeno o las galaxias. Aquí “no relativista” significa que en el marco comoving, en el que el flujo promedio de polvo se desvanece, todas las partículas de polvo tienen |v| << 1. ¿Cuál es el tensor estres-energía asociado con el polvo?

Dado que el polvo es no relativista, podemos obtener el límite newtoniano usando unidades en las que c ≠ 1, y dejando que c se acerque al infinito. En las coordenadas cartesianas, los componentes de la tensión-energía tienen unidades que hacen que escalen como

\[T^{\mu \nu} \propto \begin{pmatrix} 1 & \frac{1}{c} & \frac{1}{c} & \frac{1}{c} \\ \frac{1}{c} & \frac{1}{c^{2}} & \frac{1}{c^{2}} & \frac{1}{c^{2}} \\ \frac{1}{c} & \frac{1}{c^{2}} & \frac{1}{c^{2}} & \frac{1}{c^{2}} \\ \frac{1}{c} & \frac{1}{c^{2}} & \frac{1}{c^{2}} & \frac{1}{c^{2}} \end{pmatrix}\]

En el límite de c → ∞, por lo tanto, podemos tomar la única fuente de campos gravitacionales para ser T ^tt, que en la gravedad newtoniana debe ser la densidad de masa\(\rho\), por lo que

\[T^{\mu \nu} = \begin{pmatrix} \rho & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \ldotp\]

Bajo un impulso de Lorentz por v en la dirección x, la ley de transformación del tensor da

\[T^{\mu' \nu'} = \begin{pmatrix} \gamma^{2} \rho & \gamma^{2} v \rho & 0 & 0 \\ \gamma^{2} v \rho & \gamma^{2} v^{2} \rho & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \ldotp\]

El factor general de\(\gamma^{2}\) surge debido a la combinación de dos efectos: la masa-energía de cada partícula de polvo se incrementa en un factor de\(\gamma\), y la contracción de longitud también multiplica la densidad de las partículas de polvo por un factor de\(\gamma\). En el límite de pequeños aumentos, el tensor de energía de estrés se convierte en

\[T^{\mu' \nu'} \approx \begin{pmatrix} \rho & v \rho & 0 & 0 \\ v \rho & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \ldotp\]

Esto motiva la interpretación de los componentes espacio-tiempo de T como el flujo de masa-energía a lo largo de cada eje. En el marco cebado, la masa-energía con densidad\(\rho\) fluye en la dirección x a la velocidad v, de manera que la velocidad a la que la masa-energía pasa a través de una ventana del área A en el plano y − z viene dada por\(\rho vA\).

Esto también es consistente con nuestra imposición de la propiedad libre de divergencias, por la cual esencialmente estábamos declarando T tx como la velocidad de flujo de T ^tt.

Ejemplo 2: El centro de masa-energía

En la mecánica newtoniana, para el movimiento en una dimensión, el momento total de un sistema de partículas viene dado por p _tot = Mv _cm, donde M es la masa total y v _cm la velocidad del centro de masa. ¿Existe tal relación en la relatividad?

Dado que la masa y la energía son equivalentes, esperamos que el equivalente relativista del centro de masa tenga que ser un centro de masa-energía.

También debe quedar claro que un centro de masa-energía sólo puede definirse bien para una región del espacio-tiempo que sea lo suficientemente pequeña para que los efectos debidos a la curvatura sean despreciables. Por ejemplo, podemos tener modelos cosmológicos en los que el espacio es finito, y se expande como la superficie de un globo que está siendo volado. Si el modelo es homogéneo (no hay “puntos especiales” en la superficie del globo), entonces no hay punto en el espacio que pueda ser un centro. (Un globo real tiene un centro, pero en nuestra metáfora solo la superficie esférica del globo se traslada al espacio físico). El tema fundamental aquí es el mismo geométrico que nos llevó a concluir que no existe una conservación global de la masa-energía en la relatividad general (ver sección 4.5). En un espacio-tiempo curvo, el transporte paralelo depende de la ruta, por lo que no podemos definir inequívocamente una forma de agregar vectores que ocurren en diferentes lugares. El centro de masa está definido por una suma de vectores de posición. De estas consideraciones concluimos que el centro de masa-energía sólo está bien definido en la relatividad especial, no en la relatividad general.

Por simplicidad, limitémonos a 1+1 dimensiones, y adoptemos un marco de referencia en el que el centro de masa esté en reposo en x = 0.

Dado que T ^tt se interpreta como la densidad de masa-energía, la posición del centro de masa debe estar dada por

\[0 = \int x T^{tt} dx \ldotp\]

Por analogía con la relación newtoniana p _tot = Mv _cm, veamos qué sucede cuando nos diferenciamos con respecto al tiempo. La velocidad del centro de masa es entonces 0 =\(\frac{dx_{cm}}{dt} = \int \partial_{t} T^{tt} x dx\). Aplicando la propiedad libre de divergencias\(\partial_{t} T^{tt} + \partial_{x} T^{tx} = 0\), ésta se convierte en 0 =\(− \int \partial_{x} T^{tx} x dx\). La integración por partes nos da finalmente

\[0 = \int T^{tx} dx \ldotp\]

Ya hemos interpretado T ^tx como la velocidad de flujo de masa-energía, que es otra forma de describir el impulso. Por lo tanto, podemos interpretar T ^tx como la densidad de impulso, y el lado derecho de esta ecuación como el impulso total. La interpretación es que el centro de masa-energía de un sistema está en reposo si y sólo si tiene cero impulso total.

Supongamos, por ejemplo, que preparamos una varilla metálica uniforme para que un extremo esté caliente y el otro frío. Luego lo depositamos en el espacio exterior, inicialmente inmóvil en relación con algún observador. Si bien la varilla en sí es uniforme, su masa-energía es muy poco uniforme, por lo que su centro de masa-energía debe ser desplazado un poquito del centro, hacia el extremo caliente. A medida que la varilla se acerca al equilibrio térmico, el observador ve que se acelera muy ligeramente y luego vuelve a descansar, ¡para que su centro de masa-energía permanezca fijo! Un caso aún más extraño se describe en el ejemplo 9.

Dado que el tensor de Einstein es simétrico, la ecuación de campo de Einstein requiere que el tensor de tensión-energía también sea simétrico. Es tranquilizador que según el ejemplo 1 el tensor es simétrico para el polvo, y que la simetría se conserva por cambios de coordenadas y por superposiciones de fuentes. Además del polvo, las otras fuentes de gravedad cosmológicamente significativas son la radiación electromagnética y la constante cosmológica, y también se puede comprobar que éstas dan simetría. Belinfante señaló en 1939 que la simetría parecía fallar en el caso de campos con espín intrínseco, pero encontró que este problema podría evitarse modificando la forma previamente asumida de conectar T a las propiedades del campo. Esto demuestra que puede ser bastante sutil interpretar el tensor estres-energía y conectarlo con observables experimentales. Para más información sobre esta conexión, y el caso de los campos electromagnéticos, véanse los ejemplos 7 y 8.

En el ejemplo 1, encontramos que T ^xt tenía que interpretarse como el flujo de T ^tt (es decir, el flujo de masa-energía) a través del eje x. La invarianza de Lorentz requiere que tratemos simétricamente t, x, y z, y esto nos obliga a adoptar la siguiente interpretación: T ^{\(\mu \nu\)}, donde\(\mu\) es espacial, es el flujo de la densidad del cuatro vector masa-energía en la dirección µ. En el marco comoving, en coordenadas cartesianas, esto significa que T ^xx, T ^yy y T ^zz deben interpretarse como presiones. Por ejemplo, T ^xx es el flujo en la dirección x del impulso x. Esta es simplemente la presión, P, que se ejercería sobre una superficie con su normal en la dirección x, así que en el marco comoving tenemos T ^{\(\mu \nu\)}= diag (\(\rho\), P, P, P). Para un fluido que no está en equilibrio, la presión no necesita ser isotrópica, y la tensión ejercida por el fluido no necesita ser perpendicular a la superficie sobre la que actúa. Los componentes espacio-espaciales de T serían entonces el tensor de tensión clásico, cuyos elementos diagonales son la presión anisotrópica, y cuyos elementos fuera de la diagonal son el esfuerzo cortante. Esta es la razón para llamar a T el tensor estres-energía.

La predicción de la relatividad general es entonces que la presión actúa como una fuente gravitacional con exactamente la misma fuerza que la densidad masa-energía. Esto tiene importantes implicaciones para la cosmología, ya que el universo primitivo estuvo dominado por la radiación, y un gas fotón tiene P =\(\frac{\rho}{3}\) (ejemplo 14).

Pruebas Experimentales

Pero, ¿cómo sabemos que esta predicción es incluso correcta? ¿Se puede verificar en el laboratorio? La prueba clásica de laboratorio de la fuerza de una fuente gravitacional es el experimento Cavendish de 1797, en el que se utilizó un balance de torsión para medir las muy débiles atracciones gravitacionales entre las esferas metálicas. Podríamos probar este aspecto de la relatividad general haciendo un experimento Cavendish con cajas llenas de fotones, para que la presión sea del mismo orden de magnitud que la masa-energía. Desafortunadamente, esto es completamente poco práctico, ya que tanto P como\(\rho\) para una caja bien iluminada son ridículamente pequeños en comparación con\(\rho\) para una bola de metal.

Figura_8.1.1b.png” />

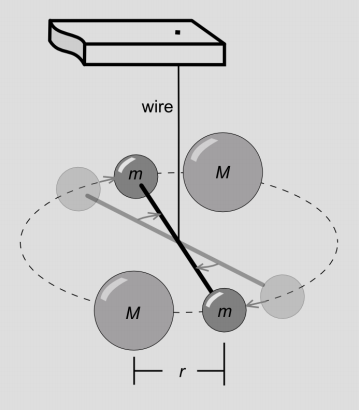
Figura\(\PageIndex{1}\) - Un balance Cavendish, utilizado para determinar la constante gravitacional.

Sin embargo, la repulsiva presión electromagnética dentro de un núcleo atómico es bastante grande para los estándares ordinarios — ¡alrededor de 10 ³³ Pa! Para ver qué tan grande es esto comparado con la densidad de masa nuclear de\(\rho ∼ 10^{18}\) kg/m ³, necesitamos tomar en cuenta el factor de c ² ≠ 1 en unidades SI, siendo el resultado que\(\frac{P}{\rho}\) es de aproximadamente 10 ⁻², que no es demasiado pequeño. Así, si medimos las interacciones gravitacionales de núcleos con diferentes valores de\(\frac{P}{\rho}\), deberíamos poder probar esta predicción de relatividad general. Esto se realizó en un experimento de tesis doctoral de Princeton realizado por Kreuzer ¹ en 1966.

Antes de poder describir e interpretar adecuadamente el experimento de Kreuzer, necesitamos distinguir los diferentes tipos de masa que en principio podrían ser diferentes entre sí en una teoría de la gravedad. Ya nos encontramos con la distinción entre masa inercial y gravitacional, que los experimentos de Eötvös muestran que equivale a aproximadamente una parte en 10 ¹². Pero también existe una distinción entre la masa gravitacional activa de _un objeto m a, que mide su capacidad para crear campos gravitacionales, y su masa gravitacional pasiva mp, que mide la fuerza que siente cuando se coloca en un campo generado externamente. Para experimentos que utilizan objetos materiales a escala de laboratorio a velocidades no relativistas, se aplica el límite newtoniano, y podemos pensar en la masa gravitacional activa como un escalar, con una densidad T ^tt =\(\rho\).

Para entender cómo esto se relaciona con la presión como fuente de campos gravitacionales, es útil considerar un caso donde P es aproximadamente lo mismo que\(\rho\), lo que ocurre para la luz. La luz es inherentemente relativista, por lo que el concepto newtoniano de una masa gravitacional escalar se descompone, pero aún podemos usar la “masa” entre comillas para hablar cualitativamente sobre la participación activa y pasiva de una onda electromagnética en los efectos gravitacionales. Los experimentos muestran que la relatividad general predice correctamente la desviación de la luz por el sol a aproximadamente una parte en 10 ⁵ (sección 6.2). Este es el equivalente electromagnético de un experimento de Eötvös; muestra que la relatividad general predice lo correcto sobre la proporción entre las “masas” gravitacionales inerciales y pasivas de una onda de luz. Ahora supongamos que la relatividad general estaba equivocada, y la presión no era una fuente de campos gravitacionales. Esto provocaría una disminución drástica en la “masa” gravitacional activa de una onda electromagnética.

El experimento de Kreuzer en realidad se ocupó de campos eléctricos estáticos dentro de núcleos, no de ondas electromagnéticas, pero todavía está claro qué debemos esperar en general: si la presión no actúa como fuente gravitacional, entonces la relación\(\frac{m_{a}}{m_{p}}\) debería ser diferente para diferentes núcleos. Específicamente, debería ser menor para un núcleo con un número atómico Z mayor, en el que las presiones electrostáticas son mayores.

Kreuzer realizó un experimento de Cavendish, Figura 8.1.2, utilizando masas compuestas por dos sustancias diferentes. La primera sustancia fue el teflón. La segunda sustancia fue una mezcla de los líquidos tricloroetileno y dibromoetano, con las proporciones elegidas para dar una densidad lo más cercana posible a la del teflón. El teflón es 76% de flúor en peso, y el líquido es 74% bromo. El flúor tiene número atómico Z = 9, bromo Z = 35, y dado que la fuerza electromagnética tiene un largo alcance, la presión dentro de un núcleo escala hacia arriba aproximadamente como Z ^1/3 (porque cualquier protón dado es actuado por Z − 1 otros protones, y el tamaño de un núcleo escala como Z 1/3, entonces\(P \propto \frac{Z}{(Z^{1/3})^{2}}\). La masa sólida se sumergió en el líquido, y el campo gravitacional combinado del sólido y el líquido se detectó mediante una balanza Cavendish.

Figura\(\PageIndex{2}\) - Un diagrama simplificado de la modificación de Kreuzer. La masa de teflón móvil se sumerge en un líquido con casi la misma densidad.

Idealmente, se formularía la mezcla líquida de manera que su densidad de pasivemasa fuera exactamente igual a la del teflón, según lo determinado por la flotabilidad. Cualquier oscilación en el par medido por el equilibrio Cavendish indicaría entonces una inequivalencia entre la masa gravitacional activa y pasiva.

Figura_8.1.3b.png” />

Figura\(\PageIndex{3}\) - El experimento de Kreuzer. 1. Hay dos masas pasivas, P, y una masa activa A que consiste en un solo cilindro de teflón de 23 cm de diámetro sumergido en un fluido. El cilindro de teflón es impulsado hacia adelante y hacia atrás con un periodo de 400 s. La deflexión resultante del haz de torsión es monitoreada por una palanca óptica y cancelada activamente por fuerzas electrostáticas de las placas del condensador (no mostradas). El voltaje requerido para esta cancelación activa es una medida del par ejercido por A en la viga de torsión. 2. Masa activa en función de la temperatura. 3. Masa pasiva en función de la temperatura. Tanto en 2 como en 3, la temperatura se mide en unidades de ohmios, es decir, las unidades no calibradas de un termistor que se sumergió en el líquido.

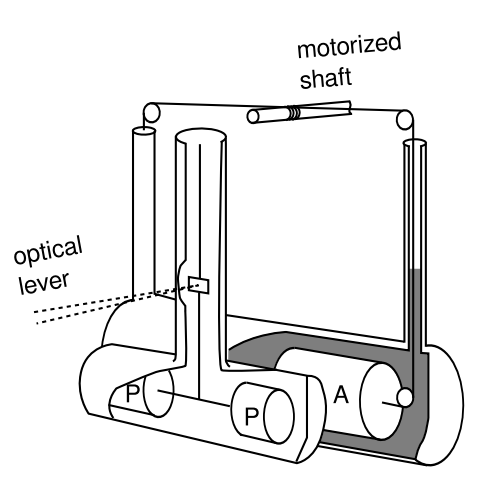
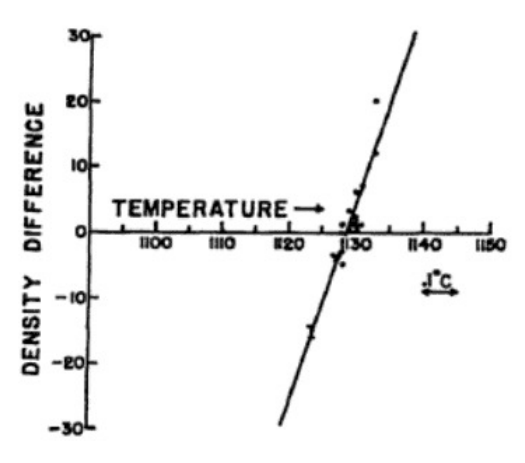
En realidad, las dos sustancias involucradas tuvieron diferentes coeficientes de expansión térmica, por lo que ligeras variaciones en la temperatura hicieron que sus densidades de masa pasiva fueran desiguales. Por lo tanto, Kreuzer midió tanto la fuerza de flotación como el par gravitacional en función de la temperatura. Determinó que éstas se convirtieron en cero a la misma temperatura, hasta dentro de errores experimentales, lo que verificó la equivalencia de la masa gravitacional activa y pasiva con dentro de cierta precisión,

\[m_{p} \propto m_{a}\]

a dentro de 5 × 10 ⁻⁵.

_{Kreuzer pretendía este esfuerzo sólo como una prueba de m p ∝ m a, pero fue reinterpretado en 1976 por Will ² como una prueba del acoplamiento de fuentes a campos gravitacionales según lo predicho por la relatividad general y otras teorías de la gravedad.} Crudamente, ya hemos argumentado que mp ∝ ma dependería de las sustancias si la presión no se acoplara a los campos gravitacionales. En realidad se llevó a cabo un cálculo más cuidadoso, del cual presento un resumen simplificado. Supongamos que la presión no contribuye tanto a los campos gravitacionales como lo afirma la relatividad general; su acoplamiento se reduce en un factor 1 − x, donde x = 0 en la relatividad general. ³ Will considera un modelo que consiste en partículas puntiformes que interactúan a través de fuerzas eléctricas estáticas, y muestra que para tal sistema,

\[m_{a} = m_{p} + \frac{1}{2} x U_{e},\]

donde U _e es la energía eléctrica. El experimento de Kreuzer requiere entonces |x| < 6 × 10 ⁻², lo que significa que la presión sí contribuye a los campos gravitacionales según lo predicho por la relatividad general, dentro de una precisión del 6%.

Nota

En la notación de Will,\(\zeta_{4}\) mide el acoplamiento no estándar a la presión,\(\zeta_{3}\) a la energía interna y\(\zeta_{1}\) a la energía cinética. Al requerir que los modelos de partículas puntuales coincidan con modelos de fluido perfecto, se obtiene\((−\frac{2}{3}) \zeta_{1} = \zeta_{3} = − \zeta_{4} = x\).

Una de las formas importantes en que el cálculo de Will va más allá de mi crudo argumento anterior es que muestra que cuando x = 0, como lo hace para la relatividad general, el término de corrección\(\frac{xU_{e}}{2}\) desaparece, y m _a = m _p exactamente. Esto se interpreta de la siguiente manera. Que se haga referencia a un núcleo de bromo con una M mayúscula, flúor con la minúscula m. Entonces, cuando un núcleo de bromo y un núcleo de flúor interactúan gravitacionalmente a una distancia r, se aplica la aproximación newtoniana, y la fuerza interna total que actúa sobre el par de núcleos tomados como un todo es igual\(\frac{m_{p} M_{a} − M_{p} m_{a}}{r^{2}}\) (en unidades donde la constante gravitacional newtoniana G es igual a 1). Esto desaparece sólo si m _p M _a − M _p m _a = 0, lo que equivale a\(\frac{m_{p}}{M_{p}} = \frac{m_{a}}{M_{a}}\). Si esta proporcionalidad falla, entonces el sistema viola la tercera ley de Newton y la conservación del impulso; su centro de masa se acelerará a lo largo de la línea que conecta los dos núcleos, ya sea en la dirección de M o en la dirección de m, dependiendo del signo de x.

Así, la desaparición del término de corrección nos\(\frac{xU_{e}}{2}\) dice que la relatividad general predice la conservación exacta del impulso en esta interacción. Esto es reconfortante, pero un poco sorprendente de cara. La gravedad newtoniana trata el masivo activo y pasivo de manera perfectamente simétrica, de manera que existe una perfecta garantía de conservación del impulso. Pero la relatividad los incorpora de una manera completamente asimétrica, por lo que no hay razón obvia para que debamos tener una perfecta conservación del impulso. De hecho no tenemos ninguna garantía general de conservación del impulso, ya que, como se discute en la sección 4.5, el lenguaje de la relatividad general ni siquiera nos da los símbolos que necesitaríamos para afirmar una ley de conservación global para un vector. La relatividad general, sin embargo, permite leyes locales de conservación. Tendremos conservación local de energía masiva e impulso siempre que la divergencia del tensor estres-energía se\(\nabla_{b} T^{ab}\) desvanezca.

Bartlett y van Buren ⁴ utilizaron esta conexión con la conservación del impulso en 1986 para derivar un límite más estricto en x Dado que la luna tiene una distribución asimétrica de hierro y aluminio, una x distinta de cero provocaría que tuviera una aceleración anómala a lo largo de cierta línea. Debido a que el alcance del láser lunar proporciona datos extremadamente precisos sobre la órbita de la luna, la restricción se ajusta a |x| < 1 × 10 ⁻⁸.

Figura\(\PageIndex{4}\) - La misión Apolo 11 dejó atrás este espejo, que en esta foto muestra el reflejo del cielo negro. El espejo se utiliza para mediciones de alcance láser lunar, que tienen una precisión de aproximadamente un centímetro.

Estas son pruebas de las predicciones de la relatividad general sobre los campos gravitacionales generados por la presión de un campo eléctrico estático. Además, hay confirmación indirecta (sección 8.2) de que la relatividad general es correcta cuando se trata de ondas electromagnéticas.

Referencias

¹ Kreuzer, Phys. Rev. 169 (1968) 1007

² Will, “Masa activa en la gravedad relativista: interpretación teórica del experimento de Kreuzer”, Ap. J. 204 (1976) 234, disponible en línea en adsabs. harvard.edu. Una revisión más amplia de las pruebas experimentales de relatividad general se da en Will, “La confrontación entre la relatividad general y el experimento”, relatividad.livingreviews.org/articles/LRR-2006-3/. El experimento de Kreuzer se discute en la sección 3.7.

⁴ Phys. Rev. Let. 57 (1986) 21. El resultado se resume en la sección 3.7 de la revisión de Will.