12.8: Las Funciones Termodinámicas para Otras Sustancias
- Page ID
- 127751
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Cálculo del cambio en las funciones termodinámicas de cualquier sustancia yendo reversiblemente de P l V 1 T 1 a P 2 V 2 T 2.
Lo primero reconfortante a tener en cuenta es que SUHAG son todas funciones estatales, y por lo tanto el cambio en sus valores es independiente de la ruta.
Entropía.
La entropía es una función de estado (i.e., de PVT), pero como las PVT se relacionan a través de la ecuación de estado, es necesario especificar solo dos de estas cantidades. Así, por ejemplo, si expresamos S en función de T y P, los incrementos infinitesimales en estos darán lugar a un incremento infinitesimal en S dado por
\[d S=\left(\frac{\partial S}{\partial T}\right)_{P} d T+\left(\frac{\partial S}{\partial P}\right)_{T} d P\]
Ahora\(\left(\frac{\partial S}{\partial T}\right)_{P}\) es (para un proceso reversible)\(\frac{C_{P}}{T}\) (ver ecuación 12.7.5), y\(\left(\frac{\partial S}{\partial P}\right)_{T}\) es (por una relación Maxwell) igual a\(-\left(\frac{\partial V}{\partial T}\right)_{P}\). Si conocemos C P en función de la temperatura, y, si conocemos la ecuación de estado, ahora podemos calcular
\[S_{2}-S_{1}=\int_{T_{1}}^{T_{2}} C_{P} \frac{d T}{T}-\int_{P_{1}}^{P_{2}}\left(\frac{\partial V}{\partial T}\right)_{P} d P\]
Esto nos permitirá calcular el cambio en la entropía de una sustancia siempre que sepamos cómo varía la capacidad calorífica con la temperatura y siempre que sepamos la ecuación de estado.
Para un gas ideal\(\left(\frac{\partial V}{\partial T}\right)_{P}=R / P\), y así obtenemos, para un gas ideal
\[S_{2}-S_{1}=\int_{T_{1}}^{T_{2}} C_{P} \frac{d T}{T}-R \ln \left(P_{2} / P_{1}\right).\]
Si queremos expresar el incremento de la entropía en términos del cambio de temperatura y volumen, y de C V, podemos usar P V = RT y C P = C V + R para obtener
\[ S_{2}-S_{1}=\int_{T_{1}}^{T_{2}} C_{V} \frac{d T}{T}+R \ln \left(V_{2} / V_{1}\right)\]
Esto concuerda con lo que teníamos en el apartado anterior para una expansión isotérmica.
Aquí hay otra forma o llegando a la ecuación 12.9.4. Queremos encontrar el cambio en la entropía de un mol de un gas ideal al pasar de (P 1, V 1, T 1) a (P 2, V 2, T 2). Dado que el cambio en la entropía es independiente de la ruta, podemos elegir cualquier ruta simple para la que el cálculo sea fácil. Vamos a ir a volumen constante de (P 1, V 1, T 1) a (P 3, V 1, T 2) y luego a temperatura constante de (P 3, V 1, T 2) a (P 2, V 2, T 2).
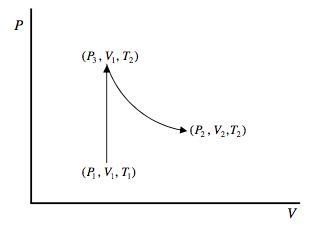
Para pasar de (P 1, V 1, T 1) a (P 3, V 1, T 2), el gas tiene que absorber una cantidad de calor\(\int_{T_{1}}^{T_{2}} C_{V} d T\), y así su entropía aumenta en\(\int_{T_{1}}^{T_{2}} C_{V} \frac{d T}{T}\). Para pasar de (P 3, V 1, T 2) a (P 2, V 2, T 2). El gas sí funciona RT 2 ln (V 2/V 1) sin ningún cambio en la energía interna (porque la energía interna de un gas ideal a temperatura constante es independiente de su volumen), y por lo tanto absorbe esta cantidad de calor. Por lo tanto su entropía aumenta en R ln (V 2/V 1). Así llegamos de nuevo a la ecuación 12.9.4.
Ejemplo: Si la sustancia es un gas monatómico ideal, entonces\(C_{P}=\frac{5}{2} R\). A partir de esto calculamos
\[S_{2}-S_{1}=\frac{5}{2} R \ln \left(\frac{T_{2}}{T_{1}}\right)-R \ln \left(\frac{P_{2}}{P_{1}}\right)=R \ln \left[\left(\frac{T_{2}}{T_{1}}\right)^{5 / 2} \frac{P_{1}}{P_{2}}\right].\]
Ejercicio: Pasar por el mismo análisis, pero partiendo de S = S (T, V). Demuestre que el resultado que obtiene para un gas ideal es el mismo que el anterior. También, por supuesto, necesariamente será lo mismo para cualquier sustancia, aunque la igualdad de la expresión que se obtiene con la ecuación 12.9.2 puede no ser inmediatamente aparente.
Ejercicio: La presión y el volumen de un gas monatómico ideal se duplican ambos. ¿Cuál es la relación entre la nueva temperatura y la antigua? ¿Cuál es el incremento en la entropía molar?
(Hago la respuesta 2.31 × 10 4 J kmole −1 K −1.) Ahora prueba el mismo problema con un gas diatómico ideal. (Hago la respuesta 3.46 × 10 4 J kmole −1 K −1.)
Energía Interna y Entalpía
Estos se pueden calcular si sabemos cómo varían C V y C P con la temperatura, porque, por definición, C V = (U /T) V y C P = (H/ T) P.
Por lo tanto
\[U_{2}-U_{1}=\int_{T_{1}}^{T_{2}} C_{V} d T\]
y
\[H_{2}-H_{1}=\int_{T_{1}}^{T_{2}} C_{P} d T.\]
Funciones de Helmholtz y Gibbs
Desde A = U − TS, tenemos
\[A_{2}-A_{1}=U_{2}-U_{1}-T_{2}\left(S_{2}-S_{1}\right)-S_{1}\left(T_{2}-T_{1}\right).\]
En el caso especial de un gas ideal, obtenemos
\[A_{2}-A_{1}=\int_{T_{1}}^{T_{2}} C_{V} d T-T_{2} \int_{T_{1}}^{T_{2}} \frac{C_{\mathrm{V}} d T}{T}-R T_{2} \ln \left(V_{2} / V_{1}\right)-S_{1}\left(T_{2}-T_{1}\right).\]
Desde G = H − TS, tenemos
\[G_{2}-G_{1}=H_{2}-H_{1}-T_{2}\left(S_{2}-S_{1}\right)-S_{1}\left(T_{2}-T_{1}\right)\]
En el caso especial de un gas ideal, obtenemos
\[G_{2}-G_{1}=\int_{T_{1}}^{T_{2}} C_{p} d T-T_{2} \int_{T_{1}}^{T_{2}} \frac{C_{P} d T}{T}-R T_{2} \ln \left(P_{1} / P_{2}\right)-S_{1}\left(T_{2}-T_{1}\right).\]
Existe, sin embargo, una seria dificultad con las ecuaciones 12.9.9 y 12.9.11, en que, para calcular el cambio en las funciones de Helmholtz y Gibbs, necesitamos conocer la entropía absoluta inicial S1.


