14: La ecuación Clausius-Clapeyron

Antes de comenzar este capítulo, probablemente sería una buena idea releer las Secciones 9.2 y 9.3 del Capítulo 9.

La ecuación Clausius-Clapeyron relaciona el calor latente (calor de transformación) de vaporización o condensación con la velocidad de cambio de la presión de vapor con la temperatura. O, en el caso de una transformación sólido-líquido, relaciona el calor latente de fusión o solidificación con la velocidad de cambio del punto de fusión con la presión.

Imaginemos un vapor en equilibrio con su líquido retenido en un cilindro por un pistón, a una temperatura constante —es decir, la temperatura a la que el líquido y el vapor están en equilibrio— es decir, el punto de ebullición (o condensación) para esa presión. Imaginamos que el pistón se sacará, a temperatura constante; el líquido se evapora y la presión permanece constante. Si el pistón es empujado hacia adentro, el vapor se condensa, a temperatura y presión constantes. Durante este proceso la presión y la temperatura permanecen constantes, por lo que la energía libre de Gibbs del sistema es constante.

Deje que G ₁ sea la energía específica libre de Gibbs para el líquido

y G ₂ sea la energía específica libre de Gibbs para el vapor.

Supongamos que una masa dm del líquido se vaporiza, de manera que la energía libre de Gibbs para el líquido disminuye en G ₁ dm y la energía libre de Gibbs para el vapor aumenta en G ₂ dm. Pero la energía libre de Gibbs para el sistema es constante. Esto por lo tanto muestra que, cuando tenemos un líquido en equilibrio con su vapor (es decir, en su punto de ebullición) las energías libres de Gibbs específicas de líquido y vapor son iguales. (Lo mismo es cierto, por supuesto, para las energías libres molares de Gibbs.) Es decir:

\[H_{1}-T S_{1}=H_{2}-T S_{2}\]

o

\[ T\left(S_{2}-S_{1}\right)=H_{2}-H_{1},\]

en el que la entalpía y la entropía son específicas. El lado izquierdo es el calor latente específico de vaporización, y ya sabíamos por el Capítulo 9 que esto era igual a la diferencia en las entalpías específicas de líquido y vapor.

También se puede escribir la igualdad de las energías libres de Gibbs específicas de líquido y vapor

\[U_{1}-T S_{1}+P V_{1}=U_{2}-T S_{2}+P V_{2},\]

o

\[T\left(S_{2}-S_{1}\right)=\left(U_{2}-U_{1}\right)+P\left(V_{2}-V_{1}\right).\]

Esto demuestra que el calor latente de vaporización entra en dos cosas: Aumentar la energía interna tras la vaporización (especialmente el aumento de la energía potencial a medida que las moléculas se separan entre sí) y el trabajo PdV realizado contra la presión externa a medida que aumenta el volumen. Así podríamos dividir el calor latente en un calor latente interno y un calor latente externo.

En lo anterior, imaginamos que algún líquido se vaporizó a medida que retirábamos el pistón. Ahora imaginemos que hacemos que algún líquido se vaporice ya que agregamos algo de calor a volumen constante. Las energías libres específicas de Gibbs de líquido y vapor aumentan ambas, pero aumentan en la misma cantidad porque, como hemos visto, cuando un líquido y su vapor están en equilibrio en el punto de ebullición, sus energías libres específicas de Gibbs son iguales. Así

\[-S_{1} d T+V_{1} d P=-S_{2} d T+V_{2} d P,\]

o

\[\frac{d P}{d T}=\frac{S_{2}-S_{1}}{V_{2}-V_{1}}.\]

El lado izquierdo es la tasa de incremento de la presión de vapor con la temperatura, mientras que S ₂ − _S1 es igual a L/T, donde L es el calor latente específico de vaporización. Así llegamos a la ecuación Clausius-Clapeyron:

\[\frac{d P}{d T}=\frac{L}{T\left(V_{2}-V_{\mathrm{L}}\right)}.\]

Ejemplo: A 100 ^o C la tasa de incremento de la presión de vapor del vapor es de 27.1 mm Hg por grado Celsius, y un gramo de vapor ocupa 1674 cm ³. ¿Cuál es el calor latente específico de vaporización?

Respuesta:\(L=T\left(V_{2}-V_{1}\right) \frac{d P}{d T}\).

\( T=373.15 \mathrm{K} . \quad V_{2}-V_{1}=1.673 \mathrm{m}^{3} \mathrm{kg}^{-1}\).

\( \frac{d P}{d T}=1.36 \times 10^{4} \times 9.81 \times 2.71 \times 10^{-2}=3.616 \mathrm{PaK}^{-1}\).

De ahí

\( \underline{\underline{L=2.26 \times 10^{6} \mathrm{J} \mathrm{kg}^{-1}}}\).

El mismo argumento se puede utilizar para relacionar la tasa de cambio del punto de fusión con la presión de un sólido con su calor latente de fusión. La ecuación Clausius-Clapeyron toma entonces la forma

\[\frac{d T}{d P}=\frac{T\left(V_{2}-V_{1}\right)}{L}.\]

Para la mayoría de las sustancias, el volumen específico del líquido (V ₂) es mayor que el volumen específico del sólido (V ₁); pero para H ₂ O, Bi y Ga, V ₂ < V ₁ y dT/dP es negativo.

Ejemplo: Para el sistema de hielo-agua,

\( \begin{array}{l}{L=3.36 \times 10^{5} \mathrm{J} \mathrm{kg}^{-1}} \\ {V_{2}=10^{-3} \mathrm{m}^{3} \mathrm{kg}^{-1}} \\ {V_{1}=1.091 \times 10^{-3} \mathrm{m}^{3} \mathrm{kg}^{-1}} \\ {T=273.15 \mathrm{K}} \end{array}\)

De ahí

\( \frac{d T}{d P}=-7.4 \times 10^{-8} \mathrm{KPa}^{-1}\)

Eso es aproximadamente −7.4 × 10 ⁻³ kelvin por atmósfera

Sólidos, Líquidos, Gases, Entropía y la Función Gibbs.

De las tres fases, sólido, líquido y vapor, el sólido es el más ordenado (tiene la menor entropía) y el vapor es el más desordenado (tiene la mayor entropía). Ahora la ecuación 12.6.12a nos dice que (G /T) = −S Esto significa que, a una presión dada, la función Gibbs del vapor disminuye rápidamente con el aumento de la temperatura, mientras que la función Gibbs de un sólido disminuye relativamente lentamente. Esquemáticamente la función Gibbs de las tres fases para H ₂ O a presión atmosférica se ve así:

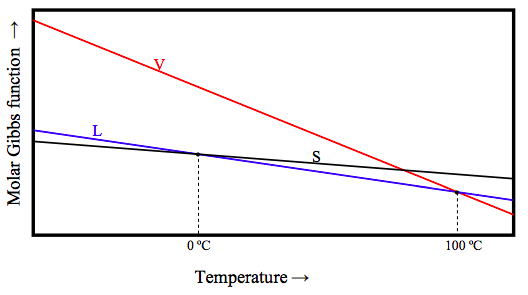
Por debajo de 0 ºC, la función Gibbs es la más baja para el sólido, y esa es la fase estable. Entre 0 ºC y 100 ºC, la función Gibbs es la más baja para el líquido, y esa es la fase estable. Por encima de los 100 ºC, la función Gibbs es la más baja para el vapor, y esa es la fase estable. A 0 ºC, la función molar de Gibbs de sólido y líquido son iguales; las dos fases que hay están en equilibrio. A 100 ºC, la función molar de Gibbs de gas y líquido son iguales; las dos fases que hay están en equilibrio.

Las pendientes e intercepciones de estas líneas varían no sólo de sustancia a sustancia, sino también, para una sustancia dada, con presión. La relación Maxwell 12.6.16,\( \left(\frac{\partial S}{\partial P}\right)_{T}=-\left(\frac{\partial V}{\partial T}\right)_{P}\), nos dice que la manera en que la entropía cambia con la presión está relacionada con el coeficiente de expansión. Para la mayoría de las sustancias (el agua entre 0 ºC y 4 ºC es una excepción), el coeficiente de expansión es positivo, por lo que esto nos dice que la entropía disminuye al aumentar la presión, y aumenta con la presión decreciente. El cambio en la entropía con la presión es mayor para el vapor, de manera que, a presiones más bajas la pendiente de la línea de vapor en la gráfica de la función de Gibbs con la temperatura será mucho más pronunciada, y la situación se verá así:

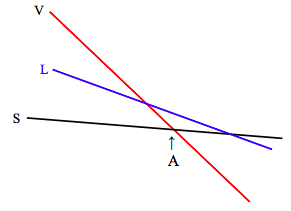
A temperaturas por debajo de A, la función Gibbs es la más baja para el sólido, y esa es la fase estable. A temperaturas superiores a A, la función Gibbs es la más baja para el vapor, y esa es la fase estable. A la presión representada en el diagrama anterior, el líquido nunca es la fase estable. La sustancia se sublima de sólido a vapor a medida que aumenta la temperatura.

A la presión correspondiente a la línea de punto triple (recuérdese mirando las figuras VI.3, VI.4 y VI.8), el diagrama se ve así:

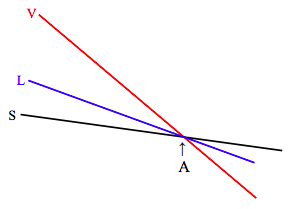
En el punto triple (A) las funciones molares de Gibbs de las tres fases son iguales, y las tres fases están en equilibrio. A medida que aumenta la temperatura desde abajo de A hasta arriba de A, la sustancia sublima directamente de sólido a vapor, como también se puede ver en la figura VI.5.