3.2: Entropía

\( \begin{aligned} d E &=T d S-p d V+\mu d N \\ &=d Q+d W_{\mathrm{conf}}+d W_{\mathrm{diss}} \\ & \geq d Q+d W_{\mathrm{conf}} \end{aligned}.\)

pero

\( d W_{\mathrm{conf}}=-p d V+\mu d N\)

entonces

\( T d S>d Q\)

donde se sostiene la igualdad para los cambios cuasistáticos.

La definición operativa de entropía es que, para un cambio cuasistático,

\[d S=\frac{d Q}{T}. \label{3.3}\]

Si entramos en un laboratorio con esta definición de entropía, el experimentalista dirá “Claro que puedo encontrar esta cantidad. Tengo termómetros; y tengo resistencias, amperímetros y voltímetros, además de un procedimiento para utilizarlos para calcular el flujo de calor”.

Para cualquier cambio (quizás cuasistático, quizás no)

\[d S \geq \frac{d Q}{T}.\]

(El cambio de entropía podría deberse al calor, podría deberse al trabajo disipativo, podría deberse a una combinación de los dos).

Entropía configuracional vs. entropía térmica

La definición operativa, termodinámica para la entropía, Ecuación\ ref {3.3}, fue descubierta de hecho antes de que fuera la definición estadística más fundamental, conceptual, (2.7). Debido a esta doble definición algunas personas tienen la idea errónea de que hay dos tipos de entropía: el tipo estadístico (“entropía configuracional”) y el tipo operativo (“entropía térmica”). Eso es falso. Estas son dos formas distintas de mirar lo mismo.

3.2 (I) Gas ideal con variables S y V.

a. Utilice la ecuación (2.32) para mostrar que para una muestra de gas ideal monatómico con un número fijo de partículas, la función de energía es

\[E(S, V)=E_{0}\left(\frac{V_{0}}{V}\right)^{2 / 3} e^{S / S_{0}},\]

donde E ₀, V ₀ y S ₀ son constantes con las dimensiones de energía, volumen y entropía.

b. Utilizar las fórmulas

\[ T(S, V)=\frac{\partial E(S, V)}{\partial S} \quad \text { and } \quad p(S, V)=-\frac{\partial E(S, V)}{\partial V}\]

para encontrar las funciones de temperatura y presión para esta muestra.

3.3 (I) Dependencia del calor y trabajo en camino

Supongamos que la muestra de gas ideal mencionada en el problema anterior sufre un cambio de un estado inicial con volumen V ₀ y entropía S ₀ a un estado final con volumen 8 V ₀ y entropía (1+ 5 ln 2) S ₀. Hay un número infinito de caminos cuasistáticos que ejecutan este cambio. Por ejemplo:

A Primero aumenta la entropía de S = S ₀ a S = (1 + 5 ln 2) S ₀, manteniendo el volumen fijo en V = V ₀, luego expandir de V = V ₀ a V = 8 V ₀, manteniendo la entropía fija en S = (1 + 5 ln 2) S ₀.

B Aumentar el volumen y la entropía simultáneamente a lo largo de la ruta

\[ S(V)=S_{0}\left[\frac{5}{3} \ln \left(\frac{V}{V_{0}}\right)+1\right].\]

C Primero expande de V = V ₀ a V = 8 V ₀, manteniendo la entropía fija en S = S ₀, luego aumenta la entropía de S = S ₀ a S = (1 + 5 ln 2) S ₀, manteniendo el volumen fijo en V = 8 V ₀.

Cada camino tiene el mismo cambio en volumen, entropía y energía, pero cada uno tendrá un calor y trabajo diferentes. (Recuerda que cada camino es cuasistático.)

a. Calcular el calor absorbido por la muestra y el trabajo realizado en la muestra para cada una de estas tres trayectorias.

b. Encuentra la diferencia Q + W para cada uno de estos tres caminos.

c. Una cuarta trayectoria desde el estado inicial hasta el estado final implica un cambio no cuasistático y la absorción de calor Q = 3 E ₀. ¿Qué trabajo se realiza en la muestra durante este cambio?

(Al inventar este problema elijo estados iniciales y finales algo peculiares, y caminos de conexión, para que las cantidades anteriores puedan calcularse analíticamente. A pesar de estas peculiaridades el principio ilustrado por el problema debe quedar claro: el calor y el trabajo dependen del camino, pero su diferencia el cambio de energía no lo hace.)

3.4 (I*) Trabajo en términos de p y V

Hasta ahora hemos considerado el trabajo y el calor en un sistema de fluidos especificado por las variables S, V y N, y a menudo hemos asumido que N es constante. Otra forma de especificar dicho sistema es a través de las variables p (presión) y V. Este problema considera procesos cuasistáticos descritos como trayectorias en el plano (p, V).

a. mostrar que el trabajo realizado en el sistema al cambiar cuasistáticamente del estado inicial (V _{i, p i}) al estado final (V _{f, p f}) a lo largo de la trayectoria que se muestra en la siguiente figura es el negativo del área bajo la curva. ¿Cuál es el trabajo realizado si el camino se recorre en sentido contrario?

b. ¿Cuál es el trabajo realizado en el sistema a través del mismo cambio a lo largo del camino de abajo?

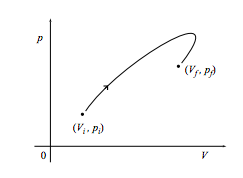
c. Finalmente, ¿cuál es el trabajo realizado en el sistema si vuelve a su punto de partida como en el ciclo que se muestra a continuación? ¿Y si el ciclo se ejecuta en cambio en sentido antihorario?

3.5 (I) Trabajo fluido

En un proceso cuasistático adiabático, una muestra de gas se expande de V _i = 1 m ³ a V _f = 8 m ³, mientras que la presión cae de p _i = 32 Pa a p _f = 1 Pa. Se observa que durante este proceso la presión y el volumen están relacionados por

\[p V^{\gamma}=\text { constant },\]

donde está la constante γ\( \frac{5}{3}\). Desde luego, este no es el único proceso que conduce de este estado inicial particular a ese estado final particular. Encontrar el trabajo total realizado en el sistema y el calor absorbido por el sistema en cada uno de los siguientes procesos cuasistáticos, todos los cuales conectan los mismos dos estados termodinámicos.

a. El proceso adiabático descrito anteriormente.

b. A presión constante, el gas se expande de V _i a V _f. (Se debe agregar calor al sistema durante esta expansión para mantener la presión constante). Entonces a volumen constante, la presión se reduce de p _i a p _f. (El calor debe extraerse del sistema durante esta etapa del proceso.)

c. El volumen se incrementa y el calor se suministra a la velocidad justa para hacer que la presión disminuya linealmente con el volumen.

d. Como en la parte (b.) pero con los dos pasos realizados en orden opuesto.