6.7: Estadísticas de Bose-Einstein

Quizás pensaste que los resultados de Fermi-Dirac fueron extraños: partículas que no interactúan formando una colección tan dura como el acero.. la temperatura ambiente siendo efectivamente cero. Espera a que veas los resultados de Bose-Einstein.

6.7.1 Teoría

Para los bosones independientes, ya sean libres o sujetos a un potencial externo, la función de número de ocupación media es

\[ b(\mathcal{E})=\frac{1}{e^{\beta(\mathcal{E}-\mu)}-1}.\]

Para comenzar a entender esta función, tenga en cuenta que

\[ \begin{array}{cc}{\text { when: }} & {\text { we have: }} \\ \hline \mathcal{E}<\mu & {b(\mathcal{E}) \text { negative }} \\ {\mathcal{E}=\mu} & {b(\mathcal{E})=\infty} \\ {\mathcal{E}>\mu} & {b(\mathcal{E}) \text { positive }}\end{array}\]

Así esta función tiene el carácter general esbozado a continuación:

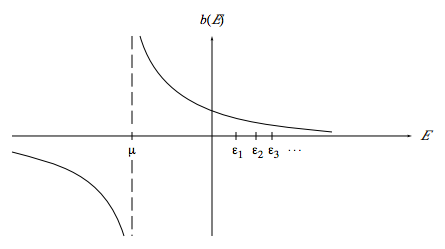
Aunque hemos escrito\( b ( \mathcal{E})\) en función de la variable continua\( \mathcal{E}\), de hecho tendremos ocasión de evaluarla solo en los valores propios de energía\(\epsilon_1,\epsilon_2, \epsilon_3,. . . , \epsilon_r,. . . \), valores propios que por supuesto difieren para diferentes potenciales externos. Parece extraño que b (E) pueda ser negativo, y de hecho esto es sólo un artefacto matemático: Recordemos que en nuestra derivación de la función Bose necesitábamos asumir que µ <\(\varepsilon_1\) para asegurar la convergencia (ver ecuación 6.35). Evaluar\( b ( \mathcal{E})\) a cualquier valor propio r siempre dará como resultado un número de ocupación promedio positivo.

El carácter de la función Bose está dominado por la singularidad at \(\mathcal{E}\)= µ, por lo que al tratar de entender la función y sus implicaciones físicas se debe ubicar primero el potencial químico. Esta sección proporcionará un recorrido por el comportamiento de Bose-Einstein con temperatura decreciente, a lo largo del cual el potencial químico se desplaza hacia la derecha. (Cuando investigamos el comportamiento de Fermi-Dirac, comenzamos en T = 0 y recorrimos con el aumento de la temperatura, por lo que el potencial químico se desplazó hacia la izquierda). Este desplazamiento hacia la derecha presenta un problema potencial, ya que a medida que disminuye la temperatura µ podría cambiar todo el camino hasta\(\epsilon_1\), y sabemos que µ < 1. Solo tendremos que seguir adelante y tomar el recorrido, siendo cautelosos porque sabemos que un bloque de carreteras µ = 1 podría aparecer justo frente a nosotros mientras vemos el campo. Con un poco de suerte µ aún no habrá llegado\(\epsilon_1\) cuando nuestro recorrido se detenga en T = 0.

Para el caso de bosones libres e independientes (sujetos a condiciones de límite periódicas), la energía a nivel del suelo es\(\epsilon_1\) = 0. El primer paso natural es encontrar µ (T, V, N) exigiendo que

\[ N=\int_{0}^{\infty} G(\mathcal{E}) b(\mathcal{E}) d \mathcal{E}.\]

Por natural que sea esto, la precaución está en orden. Recuerde que la integral anterior es una aproximación a la suma sobre niveles de energía discretos

\[ N=\sum_{r} b\left(\epsilon_{r}\right).\]

Es legítimo sustituir la suma por la integral cuando el valor de\( b ( \mathcal{E})\) cambia poco de un nivel de energía a otro. Vimos en la sección 6.5 que en el límite termodinámico, los espaciamientos del nivel de partículas libres se acercan a cero, por lo que en su mayor parte esta aproximación es excelente.. incluso exacto en el límite termodinámico. Pero hay una excepción: At\(\epsilon\) = µ, la función Bose\( b ( \mathcal{E})\) es infinita, por lo que b (µ) = ∞ es muy diferente de b (µ + δ), no importa cuán pequeño sea el número positivo δ. Por lo general podemos ignorar esta precaución, porque µ < 1 = 0. Pero si µ se acerca a 0 entonces esperamos que la aproximación (6.71) falle.

En resumen, la integral (6.71) es una buena aproximación para la suma (6.72) siempre y cuando el integrando varíe lentamente. Ahora para cualquier valor\(\mathcal{E}\) mayor que µ, puedes hacer que b (\(\mathcal{E}\)+ δ) esté muy cerca de b (E) simplemente eligiendo δ > 0 lo suficientemente pequeño. Esto es lo que sucede en el límite termodinámico. Pero para\(\mathcal{E}\) = µ, siempre hay una gran diferencia entre\( b ( \mathcal{E})\) = ∞ y b (\(\mathcal{E}\)+ δ), que es finita. Así la aproximación integral será buena siempre y cuando evitemos\(\mathcal{E}\) = µ.

En situaciones en las que la suma puede sustituirse legítimamente por la integral, tenemos

\[ N=\int_{0}^{\infty} G(\mathcal{E}) b(\mathcal{E}) d \mathcal{E}\]

\[ =V\left[\frac{\sqrt{2 m^{3}}}{2 \pi^{2} \hbar^{3}}\right] \int_{0}^{\infty} \sqrt{\mathcal{E}} \frac{1}{e^{\beta(\mathcal{E}-\mu)}-1} d \mathcal{E}.\]

El uso de la sustitución obvia\(x = \beta \mathcal{E}\) da

\[ N=V\left[\frac{\sqrt{2 m^{3}}}{2 \pi^{2} \hbar^{3}}\right]\left(k_{B} T\right)^{3 / 2} \int_{0}^{\infty} \frac{x^{1 / 2}}{e^{x} e^{-\beta \mu}-1} d x,\]

y recordar la definición (5.4) de la longitud de onda térmica de Broglie da como resultado una expresión más conveniente

\[ N=\frac{2}{\sqrt{\pi}} \frac{V}{\lambda^{3}(T)} \int_{0}^{\infty} \frac{x^{1 / 2}}{e^{x} e^{-\beta \mu}-1} d x.\]

Tenga en cuenta que la integral definida anterior no es “solo un número”.. es una función del producto βµ. No hay expresión de forma cerrada para la integral, aunque se evalúa fácilmente numéricamente y se puede encontrar en tabulaciones de funciones. Sin embargo, es fácil encontrar un límite superior analítico: Debido a que µ < 0, tenemos e ^−βµ > 1 de donde

\[ \int_{0}^{\infty} \frac{x^{1 / 2}}{e^{x} e^{-\beta \mu}-1} d x<\int_{0}^{\infty} \frac{x^{1 / 2}}{e^{x}-1} d x.\]

La expresión de la derecha es solo un número, y un poco de trabajo (ver problema 6.26) muestra que es el número

\[ \zeta\left(\frac{3}{2}\right) \frac{\sqrt{\pi}}{2},\]

donde la función zeta de Riemann está definida por

\[ \zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^{s}} \quad \text { and } \quad \zeta\left(\frac{3}{2}\right)=2.612375348 \dots\]

Entonces, ¿cómo nos ayuda este límite superior? Demuestra que

\[ N=\frac{2}{\sqrt{\pi}} \frac{V}{\lambda^{3}(T)} \int_{0}^{\infty} \frac{x^{1 / 2}}{e^{x} e^{-\beta \mu}-1} d x<\frac{V}{\lambda^{3}(T)} \zeta\left(\frac{3}{2}\right),\]

pero ¿cuál es el significado de este resultado? Recuerde que el límite superior es solo el valor de la función cuando µ = 0, que es exactamente donde esperamos un bloqueo de carretera debido a la ruptura de la aproximación integral (6.71). Nuestras esperanzas de que pudiéramos evitar el tema se han desvanecido. La avería se produce a la temperatura T ₀ que satisface

\[ N=\frac{V}{\lambda^{3}\left(T_{0}\right)} \zeta\left(\frac{3}{2}\right) \quad \text { or } \quad \lambda^{3}\left(T_{0}\right)=\zeta\left(\frac{3}{2}\right) / \rho\]

o

\[ T_{0}(\rho)=\frac{h^{2}}{2 \pi m k_{B} \zeta^{2 / 3}\left(\frac{3}{2}\right)} \rho^{2 / 3}.\]

Para temperaturas superiores a T ₀, el potencial químico se desplaza justo a medida que baja la temperatura, y la aproximación integral (6.71) es legítima (de hecho, exacta en el límite termodinámico). Pero a medida que la temperatura disminuye por debajo de T ₀, el potencial químico se adhiere a µ = 0 y se debe modificar la aproximación integral (6.71).

¿Cuál es la modificación adecuada? La función\(b(\mathcal{E})\) varía lentamente para todos los valores de\(\mathcal{E}\) except\(\mathcal{E}\) = µ, por lo que la aproximación integral es legítima para todos los niveles de energía excepto el nivel del suelo en 1 = 0 = µ. Solo para el nivel del suelo se necesita algún otro resultado, por lo que solo agregamos en la ocupación del nivel del suelo a mano:

\[ N=\left\langle n_{1}\right\rangle+\int_{0}^{\infty} G(\mathcal{E}) b(\mathcal{E}) d \mathcal{E}.\]

Ahora, ya hemos visto que cuando µ = 0 —la condición para la validez de esta ecuación—la integral se puede evaluar exactamente y tenemos

\[ N=\left\langle n_{1}\right\rangle+\frac{V}{\lambda^{3}(T)} \zeta\left(\frac{3}{2}\right).\]

Tenga en cuenta que\( \langle n_1 \rangle\) aquí no viene dada por su fórmula tradicional (6.45), porque

\[ \frac{1}{e^{\beta(\mathcal{E}-\mu)}-1}=\frac{1}{e^{0}-1}=\infty.\]

En cambio, la ecuación (6.84) es la fórmula para\( \langle n_1 \rangle \) cuando T < T ₀. La ocupación media a nivel del suelo\( \langle n_1 \rangle \) es una cantidad intensiva cuando T > T ₀ pero una cantidad extensa cuando T < T ₀.

En resumen, la ecuación de normalización correcta se divide en dos partes, a saber:

\[ N=\left\{\begin{array}{ll}{\frac{2}{\sqrt{\pi}} \frac{V}{\lambda^{3}(T)} \int_{0}^{\infty} \frac{x^{1 / 2}}{e^{x} e^{-\beta \mu}-1} d x} & {\text { for } T>T_{0}(\rho)} \\ {\left\langle n_{1}\right\rangle+\frac{V}{\lambda^{3}(T)} \zeta\left(\frac{3}{2}\right)} & {\text { for } T<T_{0}(\rho)}\end{array}\right.\]

Debemos esperar que cada parte se comporte de manera bastante diferente, es decir, esperamos un cambio repentino de comportamiento a medida que la temperatura desciende por T ₀.

¿Qué significa todo esto físicamente? Una lectura ingenua de la ecuación (6.80) sugiere un límite superior en el número de partículas que se pueden colocar en el volumen V. Esto sería sensato si las partículas fueran canicas con repulsiones de núcleo duro. ¡Pero estas son partículas que no interactúan! Seguramente podemos agregar más partículas con solo tirarlas al contenedor. De hecho podemos hacerlo, y el número de ocupación media en exceso asociado se debe al nivel que más les gusta a las partículas a bajas temperaturas, es decir, el nivel del suelo. El nivel del suelo tiene así una ocupación media mucho mayor que el primer nivel excitado, y esta rápida variación de ocupación media con energía hace inválida la aproximación de suma por integral. La desigualdad (6.80) no limita el número de partículas en el sistema: en cambio muestra el dominio dentro del cual es legítimo aproximar la suma (6.72) por la integral (6.71).

La transición abrupta a T ₀ (ρ) se llama condensación de Bose-Einstein y el material a temperaturas por debajo de T ₀ (ρ) se llama condensado de Bose. Estos términos son lamentables: evocan imágenes de un gas que se condensa en un líquido, en cuya circunstancia los átomos se separan en dos clases distintas: las del líquido y las que quedan en el vapor. Esto sugiere que en la condensación de Bose-Einstein también hay dos clases de partículas: las que están en el nivel del suelo y las que están en los niveles excitados. Esta imagen es totalmente falsa. Es incorrecto decir “una partícula está en el nivel del suelo, otra está en el cuarto nivel excitado”. En verdad, las partículas individuales no están en niveles individuales en absoluto: en cambio, todo el sistema está en un estado producido multiplicando juntas las funciones de onda de nivel individual (“bloques de construcción”) y luego simetrizándolas. La literatura de las estadísticas de Bose-Einstein está llena de afirmaciones como “a temperaturas por debajo de T ₀, cualquier partícula añadida al sistema entra en el nivel del suelo”. Tales declaraciones son erróneas. Deberían sustituirse por enunciados como “a temperaturas inferiores a T ₀, cualquier incremento en el número de partículas se produce a través de un incremento en\( \langle n_1 \rangle\), la ocupación media del nivel del suelo”. O alternativamente, “a temperaturas por debajo de T ₀, es muy probable que muchos de los bloques de construcción a partir de los cuales se construye la función de onda del sistema sean el nivel del suelo”. O nuevamente, para ser absolutamente precisos, “a temperaturas por debajo de T ₀, si se mide la energía entonces es muy probable que muchos de los bloques de construcción a partir de los cuales se construye la función propia de energía resultante sean el nivel del suelo”. Vuelva a leer el párrafo anterior —el que comienza “¿Qué significa todo esto físicamente?”. Observe que nunca necesito decir que una partícula “está en” o “entra” en un nivel dado.

6.7.2 Experimento

Referencias: M.H. Anderson, J.R. Ensher, M.R. Matthews, C.E. Wieman, E.A. Cornell, “Observación de la condensación de Bose-Einstein en un vapor atómico diluido”, Science, 269 (14 de julio de 1995) 198—201; Randall G. Hullet en Rice; Malcolm W. Browne, “Dos grupos de físicos producen materia que Einstein postuló”, New York Times, 14 de julio de 1995, página 1.

6.7.3 Problemas

6.23 Carácter de la función Bose

¿Cuáles son los límites de la función Bose\(b( \mathcal{E})\) (ecuación 6.70) como\(\mathcal{E}\) → ±∞? ¿La curvatura de la función es mayor cuando la temperatura es alta o cuando es baja?

6.24 Termodinámica del condensado de Bose

Para temperaturas inferiores a la temperatura de condensación de Bose T ₀, encuentre la energía, la capacidad calorífica y la entropía de un gas ideal de bosones espín-cero confinados a un volumen V. Escribe tus respuestas en términos de la integral adimensional

\[ I=\int_{0}^{\infty} \frac{x^{3 / 2}}{e^{x}-1} d x\]

pero no te molestes en evaluarlo. Demostrar que

\[ C_{V}=\frac{5}{2} \frac{E}{T} \quad \text { and } \quad S=\frac{5}{3} \frac{E}{T}.\]

6.25 Más termodinámica del condensado de Bose

Para el sistema del problema anterior, mostrar que

\[ F=-\frac{2}{3} E \quad \text { and } \quad p=\frac{2}{3} \frac{E}{V}.\]

De esta muestra que a bajas temperaturas, la presión de una colección de bosones libres e independientes va como p ∼ T ^5/2. (Esto siempre es menor que la presión clásica p ∼ T.)

6.26 Una integral importante para la condensación de Bose

Demostrar que

\[ \int_{0}^{\infty} \frac{x^{1 / 2}}{e^{x}-1} d x=\zeta\left(\frac{3}{2}\right) \frac{\sqrt{\pi}}{2}\]

donde

\[ \zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^{s}}.\]

Pistas:

\[ \frac{1}{e^{x}-1}=\frac{1}{e^{x}\left(1-e^{-x}\right)}=e^{-x} \sum_{n=0}^{\infty} e^{-n x} \quad \text { for } \quad x>0.\]