6.1: Modelo Ising

Template:MathJaxArovas

Definición

El modelo más simple de un sistema de interacción consiste en una red\(\CL\) de sitios, cada uno de los cuales contiene un giro\(\sigma\ns_i\) que puede ser up (\(\sigma\ns_i=+1\)) o down (\(\sigma\ns_i=-1\)). El hamiltoniano es

\[\HH=-J\sum_{\langle ij\rangle} \sigma\ns_i \,\sigma\ns_j - \mu\ns_0 H\sum_i\sigma\ns_i\ .\]

Cuando\(J>0\), la configuración preferida (energía más baja) de los giros vecinos es que están alineados,\(\sigma\ns_i\,\sigma\ns_j=+1\). La interacción se llama entonces ferromagnética. Cuando\(J<0\) la preferencia es por el antialineamiento\(\sigma\ns_i\,\sigma\ns_j=-1\), que es antiferromagnético.

Este modelo no es exactamente solucionable en general. En una dimensión, la solución es bastante sencilla. En dos dimensiones, la solución de Onsager del modelo (con\(H=0\)) se encuentra entre los resultados más celebrados en física estadística. En dimensiones superiores el sistema ha sido estudiado por simulaciones numéricas (el método de Monte Carlo) y por cálculos teóricos de campo (grupo de renormalización), pero no existen soluciones exactas.

Modelo Ising en una dimensión

Considera un anillo unidimensional de\(N\) sitios. La función de partición canónica ordinaria es entonces

\[\begin{split} Z\nd_{ring}&=\Tra e^{-\beta\HH}\\ &=\sum_{\{\sigma\ns_n\}}\prod_{n=1}^N e^{\beta J \sigma\ns_n\sigma\ns_{n+1}}\,e^{\beta\mu\ns_0 H\sigma\ns_n}\\ &=\Tra\! \big(R^N\big)\ , \end{split}\]

donde\(\sigma\ns_{N+1}\equiv\sigma\ns_1\) debido a condiciones de frontera periódicas (anillo), y dónde\(R\) hay una matriz\(2\times 2\) de transferencia,

\[\begin{split} R\ns_{\sigma\sigma'}&= e^{\beta J\sigma\sigma'}\,e^{\beta\mu\ns_0 H(\sigma+\sigma')/2}\\ &=\begin{pmatrix} e^{\beta J}\,e^{\beta\mu\ns_0 H} & e^{-\beta J} \\ e^{-\beta J} & e^{\beta J}\,e^{-\beta\mu\ns_0 H} \end{pmatrix}\\ &=e^{\beta J}\cosh(\beta\mu\nd_0 H) + e^{\beta J}\sinh(\beta\mu\ns_0 H)\,\tau^z + e^{-\beta J}\,\tau^x\ , \end{split}\]

donde\(\tau^\alpha\) están las matrices Pauli. Dado que el rastro de una matriz es invariante bajo una transformación de similitud, tenemos

\[Z(T, H,N)=\lambda_+^N+ \lambda_-^N \ ,\]

donde

\[\lambda\ns_\pm(T, H)=e^{\beta J}\cosh(\beta\mu\ns_0 H)\pm\sqrt{e^{2\beta J}\sinh^2(\beta\mu\ns_0 H) + e^{-2\beta J}}\]

son los valores propios de\(R\). En el límite termodinámico,\(N\to\infty\), y el\(\lambda_+^N\) término domina exponencialmente. Por lo tanto, tenemos

\[F(T, H,N)=-N\kT\ln\lambda\ns_+(T, H)\ .\]

A partir de la energía libre, podemos calcular la magnetización,

\[M=-\pabc{F}{ H}{T,N}={N\mu\ns_0\,\sinh(\beta\mu\ns_0 H)\over\sqrt{\sinh^2(\beta\mu\ns_0 H) + e^{-4\beta J}}}\]

y la susceptibilidad isotérmica de campo cero,

\[\xhi(T)={1\over N}\,{\pz M\over\pz H}\bigg|\nd_{ H=0}={\mu_0^2\over\kT}\,e^{2J/\kT}\ .\]

Tenga en cuenta que en el límite de no interacción\(J\to 0\) recuperamos el resultado familiar para un giro gratis. El efecto de las interacciones a baja temperatura es incrementar enormemente la susceptibilidad. En lugar de un conjunto de giros individuales independientes, el sistema se comporta efectivamente como si estuviera compuesto por grandes bloques de giros, donde el tamaño del bloque\(\xi\) es la longitud de correlación, que se derivará a continuación.

Las propiedades físicas del sistema a menudo se dilucidan mediante la evaluación de diversas funciones de correlación. En este caso, definimos

\[\begin{split} C(n)\equiv \blangle \sigma\ns_1\,\sigma\ns_{n+1}\brangle&={\Tra\big(\sigma\ns_1\,R\ns_{\sigma\ns_1\sigma\ns_2}\cdots R\ns_{\sigma\ns_n\sigma\ns_{n+1}}\,\sigma\ns_{n+1}\,R\ns_{\sigma\ns_{n+1}\sigma\ns_{n+2}}\cdots R\ns_{\sigma\ns_N\sigma\ns_1}\big) \over\Tra \big(R^N\big)}\\ &={\Tra\big(\Sigma\, R^n\, \Sigma\, R^{N-n}\big)\over \Tra \big(R^N\big)}\ , \end{split}\]

dónde\(0<n<N\) y dónde

\[\Sigma=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\ .\]

Para calcular esta relación, nos descomponemos\(R\) en términos de sus vectores propios, escribiendo

\[R=\lambda\ns_+\, \tket{+}\tbra{+} + \lambda\ns_-\, \tket{-}\tbra{-}\ .\]

Entonces

\[C(n)={\lambda_+^N\,\Sigma^2_{++} + \lambda_-^N\,\Sigma^2_{--} + \big(\lambda_+^{N-n}\,\lambda_-^n + \lambda_+^n\,\lambda_-^{N-n}\big)\,\Sigma\ns_{+-}\Sigma\ns_{-+}\over \lambda_+^N + \lambda_-^N}\ ,\]

donde

\[\Sigma\ns_{\mu\mu'}=\sexpect{\mu}{\Sigma}{\mu'}\ .\]

Campo externo cero

Consideremos el caso\(H=0\), dónde\(R=e^{\beta J} + e^{-\beta J}\,\tau^x\), dónde\(\tau^x\) está la matriz Pauli. Entonces

\[\sket{\pm}=\frac{1}{\sqrt{2}}\Big(\tket{\!\uar} \pm \tket{\!\dar}\Big)\ ,\]

los vectores propios de\(R\) son

\[\psi\nd_\pm={1\over\sqrt{2}}\begin{pmatrix} 1 \\ \pm 1 \end{pmatrix}\ , \label{evecs}\]

y\(\Sigma\ns_{++}=\Sigma\ns_{--}=0\), mientras\(\Sigma\ns_{\pm}= \Sigma\ns_{-+}=1\). Los valores propios correspondientes son

\[\lambda\ns_+=2\cosh(\beta J)\qquad,\qquad \lambda\ns_-=2\sinh(\beta J)\ .\]

La función de correlación se encuentra entonces para ser

\[\begin{split} C(n)\equiv \blangle \sigma\ns_1\,\sigma\ns_{n+1}\brangle&= {\lambda_+^{N-|n|}\,\lambda_-^{|n|}+ \lambda_+^{|n|}\, \lambda_-^{N-|n|}\over\lambda_+^N + \lambda_-^N}\\ &={\tanh^{|n|}(\beta J) + \tanh^{N-|n|}(\beta J)\over 1+ \tanh^N(\beta J)}\bvph\\ &\approx \tanh^{|n|}(\beta J)\qquad (N\to\infty)\ . \end{split}\]

Este resultado también es válido para\(n<0\), siempre y cuando\(|n|\le N\). Vemos que podemos escribir

\[C(n)=e^{-|n|/\xi(T)}\ ,\]

donde la longitud de correlación es

\[\xi(T)={1\over\ln{ctnh}(J/\kT)}\ .\]

Tenga en cuenta que\(\xi(T)\) crece como\(T\to 0\) como\(\xi\approx \half \,e^{2J/\kT}\).

Cadena con extremos libres

Cuando la cadena tiene extremos libres, hay\((N\!-\!1)\) eslabones, y la función de partición es

\[\begin{split} Z\nd_{chain}&=\sum_{\sigma,\sigma'} \big( R^{N-1}\big)\nd_{\sigma\sigma'}\\ &=\sum_{\sigma,\sigma'}\Big\{\lambda_+^{N-1}\,\psi_+(\sigma)\,\psi_+(\sigma')+\lambda_-^{N-1}\,\psi_-(\sigma)\,\psi_-(\sigma')\Big\}\ , \end{split}\]

donde\(\psi\nd_\pm(\sigma)=\sbraket{\sigma}{\pm}\). Cuando\(H=0\), hacemos uso de la Ecuación\ ref {evecs} para obtener

\[R^{N-1}={1\over 2} \begin{pmatrix} 1 &1 \\ 1 & 1 \end{pmatrix} \big(2\cosh\beta J\big)^{N-1} + {1\over 2} \begin{pmatrix} 1 & -1 \\ -1& 1 \end{pmatrix} \big(2\sinh\beta J\big)^{N-1} \ ,\]

y por lo tanto

\[Z\nd_{chain}=2^N\cosh^{N-1}(\beta J)\ .\]

Hay un truco inteligente para obtener la función de partición para la cadena Ising que equivale a un cambio de variables. Definimos

\[\nu\nd_n\equiv\sigma\nd_n\,\sigma\nd_{n+1}\qquad (n=1\,,\,\ldots\,,\,N-1)\ .\]

Así,\(\nu\nd_1=\sigma\nd_1\sigma\nd_2\)\(\nu_2=\sigma\nd_2\sigma\nd_3\), Tenga en cuenta que cada uno\(\nu\nd_j\) toma los valores\(\pm 1\). El hamiltoniano para la cadena es

\[H\nd_{chain}=-J\sum_{n=1}^{N-1}\sigma\nd_n\,\sigma\nd_{n+1}=-J\sum_{n=1}^{N-1}\nu\nd_n\ .\]

El estado del sistema está definido por las variables\(N\) Ising\(\{\sigma\nd_1\,,\,\nu\nd_1\,,\,\ldots\,,\,\nu\nd_{N-1}\}\). Tenga en cuenta que\(\sigma\nd_1\) no aparece en el hamiltoniano. Por lo tanto, el modelo que interactúa se refunde como giros de Ising\(N\!-\!1\) no interactivos, y la función de partición es

\[\begin{split} Z\nd_{chain}&={Tr}\,e^{-\beta H\nd_{chain}}\\ &=\sum_{\sigma\ns_1}\sum_{\nu\ns_1}\cdots\sum_{\nu\ns_{N-1}} e^{\beta J\nu\nd_1} e^{\beta J\nu\nd_2}\cdots e^{\beta J\nu\nd_{N-1}}\\ &=\sum_{\sigma\ns_1}\left(\sum_\nu e^{\beta J\nu}\right)^{\!\!N-1}=2^N\cosh^{N-1}(\beta J)\ . \end{split}\]

Modelo de Ising en dos dimensiones: argumento de Peierls

Acabamos de ver cómo en una dimensión, el modelo Ising nunca logra un orden de giro de largo alcance. Es decir, la función de correlación espín-espín decae asintóticamente como una función exponencial de la distancia con una longitud de correlación\(\xi(T)\) que es finita para todos\(>0\). Solo para\(T=0\) la longitud de correlación diverge. En\(T=0\), hay dos estados terrestres,\(\sket{\!\!\uar\uar\uar\uar\cdots\uar}\) y\(\sket{\!\!\dar\dar\dar\dar\cdots\dar}\). Para elegir entre estos estados terrestres, podemos especificar una condición de límite en los extremos de nuestra cadena unidimensional, donde exigimos que los giros estén arriba. Equivalentemente, podemos aplicar un campo magnético\(H\) de orden\(1/N\), que desaparece en el límite termodinámico, pero que a temperatura cero seleccionará el estado fundamental 'all up'. A temperatura finita, siempre hay una probabilidad finita de que cualquier par consecutivo de sitios\((n,n\!+\!1)\) esté en un estado de alta energía, ya sea\(\sket{\!\!\uar\dar}\) o\(\sket{\!\!\dar\uar}\). Tal configuración se denomina muro de dominio, y en sistemas unidimensionales las paredes de dominio viven en enlaces individuales. En relación con las configuraciones\(\sket{\!\!\uar\uar}\) y\(\sket{\!\!\dar\dar}\), un muro de dominio cuesta energía\(2J\). Para un sistema con muros de\(M=xN\) dominio, la energía libre es

\[\begin{split} F&=2MJ - \kT\ln{N\choose M}\\ &=N\cdot\Bigg\{2Jx + \kT\Big[ x\ln x + (1-x)\ln (1-x)\Big]\Bigg\}\ , \end{split}\]

Minimizando la energía libre con respecto a\(x\), uno encuentra\(x=1\big/\big(e^{2J/\kT}+1\big)\), por lo que la concentración de equilibrio de las paredes de dominio es finita, lo que significa que no puede haber un orden de espín de largo alcance. En una dimensión, la entropía gana y siempre hay un número termodinámicamente grande de muros de dominio en equilibrio. Y dado que la longitud de correlación para\(T>0\) es finita, cualquier condición límite impuesta en el infinito espacial no tendrá consecuencias termodinámicas ya que solo se 'sentirán' sobre un rango finito.

Como discutiremos en el siguiente capítulo, esta consideración es cierta para cualquier sistema con interacciones suficientemente cortas y una simetría global discreta. Otro ejemplo es el modelo\(q\) -state Potts,

\[H=-J\sum_{\langle ij\rangle}\delta\nd_{\sigma\ns_i,\sigma\ns_j}-h\sum_i\delta\nd_{\sigma\ns_i,1}\ .\]

Aquí, las variables de giro\(\sigma\ns_i\) toman valores en el conjunto\(\{1,2,\ldots,q\}\) en cada sitio. El equivalente de un campo magnético externo en el caso de Ising es un campo\(h\) que prefiere un valor particular de\(\sigma\) (\(\sigma=1\)en el hamiltoniano anterior). Consulte el apéndice en § 8 para una solución de matriz de transferencia del modelo unidimensional Potts.

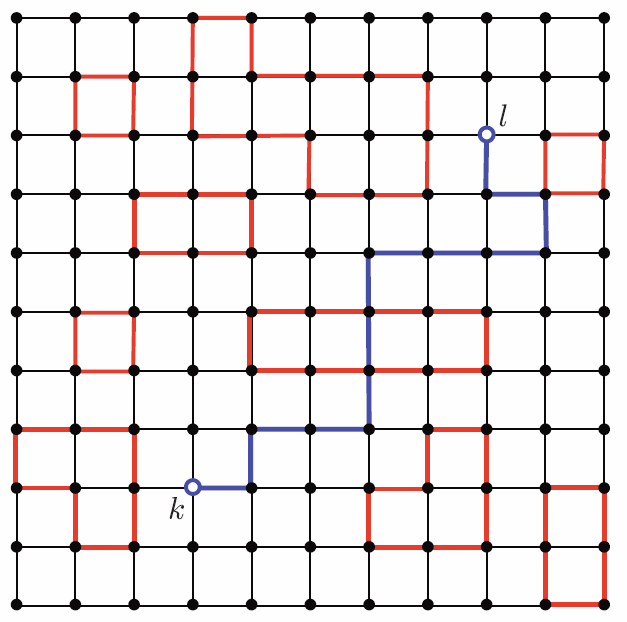
¿Qué pasa con las dimensiones más altas? Un argumento acertado debido a R. Peierls muestra que habrá una transición de fase de temperatura finita para el modelo de Ising en la celosía cuadrada ¹. Considera el modelo Ising, en campo magnético cero, sobre una celosía\(N\ns_x\times N\ns_y\) cuadrada, con\(N\ns_{x,y}\to \infty\) en el límite termodinámico. A lo largo del perímetro del sistema imponemos la condición límite\(\sigma\ns_i=+1\). Cualquier configuración de los giros puede representarse entonces de manera única de la siguiente manera. Comienza con una configuración en la que todos los giros estén arriba. A continuación, dibuje un conjunto de bucles cerrados en la celosía. Por definición, los bucles no pueden compartir ningún enlace a lo largo de sus límites, cada enlace en la celosía está asociado a lo sumo con uno de esos bucles. Ahora voltea todos los giros dentro de cada bucle de arriba a abajo. Identifique cada configuración de bucle con una etiqueta\(\Gamma\). La función de partición es

\[Z=\Tra e^{-\beta\HH}=\sum_\Gamma e^{-2\beta J L\ns_\Gamma}\ ,\]

donde\(L\ns_\Gamma\) está el perímetro total de la configuración del bucle\(\Gamma\). Los muros de dominio son ahora bucles, en lugar de enlaces individuales, pero como en el caso unidimensional, cada enlace de cada muro de dominio aporta una energía\(+2J\) relativa al estado fundamental.

Figura\(\PageIndex{1}\): Cúmulos y límites para el modelo Ising de celosía cuadrada. Panel izquierdo: una configuración\(\Gamma\) donde el giro central está arriba. Panel derecho: una configuración\(C_\gamma\circ \Gamma\) donde se han volteado los giros interiores de un nuevo bucle\(\gamma\) que contiene el giro central.

Ahora deseamos calcular la magnetización promedio del sitio central (supongamos que ambos\(N\ns_{x,y}\) son impares, por lo que hay un sitio central único). Esto viene dado por la diferencia\(P\ns_+(0)-P\ns_-(0)\), donde\(P\ns_\mu(0)= \blangle \delta\ns_{\sigma\ns_0\,,\,\mu}\brangle\) está la probabilidad de que el giro central tenga polarización de espín\(\mu\). Si\(P\ns_+(0) > P\ns_-(0)\), entonces la magnetización por sitio\(m=P\ns_+(0)-P\ns_-(0)\) es finita en el límite termodinámico, y se ordena el sistema. Claramente

\[P\ns_+(0)={1\over Z}\sum_{\Gamma \in \RSigma\ns_+} e^{-2\beta J L\ns_\Gamma}\ ,\]

donde la restricción en la suma indica que solo se van a incluir aquellas configuraciones donde el giro central es up (\(\sigma\ns_0=+1\)) (Figura\(\PageIndex{1a}\)). Del mismo modo,

\[P\ns_-(0)={1\over Z}\sum_{\widetilde\Gamma \in \RSigma\ns_-} e^{-2\beta J L\ns_{\widetilde\Gamma}}\ ,\]

donde sólo las configuraciones en\(\sigma\ns_0=-1\) las que se incluyen en la suma. Aquí hemos definido

\[\RSigma\ns_\pm=\Big\{ \Gamma\ \big|\ \sigma\ns_0=\pm \Big\}\ .\]

\(\RSigma\ns_+(\Sigma\ns_-)\)es el conjunto de configuraciones\(\Gamma\) en las que el giro central es siempre hacia arriba (abajo). Consideremos ahora la construcción en la Figura\(\PageIndex{1b}\). Cualquier configuración de bucle\({\widetilde\Gamma}\in\RSigma\ns_-\) puede asociarse con una configuración de bucle única\(\Gamma\in\RSigma\ns_+\) invirtiendo todos los giros dentro del bucle de los\({\widetilde\Gamma}\) cuales contiene el origen. Tenga en cuenta que el mapa de\({\widetilde\Gamma}\) a\(\Gamma\) es de muchos a uno. Es decir, podemos escribir\({\widetilde\Gamma}=C\ns_\gamma\circ\Gamma\), donde\(C\ns_\gamma\) vuelca los giros dentro del bucle\(\gamma\), con las condiciones que (i)\(\gamma\) contiene el origen, y (ii) ninguno de los enlaces en el perímetro de\(\gamma\) coincide con ninguno de los enlaces de los bucles constitutivos de\(\Gamma\). Denotemos este conjunto de bucles como\(\RUps\ns_{\!\Gamma}\):

\[\RUps\ns_{\!\Gamma}=\Big\{ \gamma\ :\ \hbox{$0\in{int}(\gamma)$ and $\gamma\cap\Gamma=\emptyset$} \Big\}\ .\]

Entonces

\[m=P\ns_+(0)-P\ns_-(0)={1\over Z}\sum_{\Gamma\in\RSigma\ns_+} e^{-2\beta J L\ns_\Gamma} \bigg( 1 - \sum_{\gamma\in\RUps\ns_{\!\Gamma}} e^{-2\beta J L\ns_{\gamma}}\bigg)\ .\]

Si podemos probarlo\(\sum_{\gamma\in\RUps\ns_{\!\Gamma}} e^{-2\beta J L\ns_{\gamma}}<1\), entonces lo habremos establecido\(m>0\). Preguntemos: ¿cuántos bucles\(\gamma\) hay\(\Ups\ns_{\!\Gamma}\) con perímetro\(L\)? No podemos responder exactamente a esta pregunta, pero podemos derivar un límite superior riguroso para este número, que, siguiendo a Peliti, llamamos\(g(L)\). Afirmamos que

\[g(L) < {2\over 3L}\cdot 3^L\cdot \bigg({L\over 4}\bigg)^{\!2} = {L\over 24}\cdot 3^L\ . \label{gupper}\]

Para establecer este límite, considere cualquier sitio en tal bucle\(\gamma\). Inicialmente tenemos\(4\) posibles indicaciones para proceder al siguiente sitio, pero a partir de entonces solo hay\(3\) posibilidades para cada paso posterior, ya que el bucle no puede toparse consigo mismo. Esto da\(4\cdot 3^{L-1}\) posibilidades. Pero claramente estamos superando, ya que cualquier punto del bucle podría haber sido elegido como el punto inicial, y además podríamos haber comenzado procediendo ya sea en sentido horario o antihorario. Entonces estamos justificados en dividir esto por\(2L\). Todavía estamos superando, porque no hemos contabilizado la restricción que\(\gamma\) es un bucle cerrado, ni eso\(\gamma\cap\Gamma=\emptyset\). No nos molestaremos en tratar de mejorar nuestra estimación para dar cuenta de estas limitaciones. Sin embargo, claramente estamos subcontando debido a que un bucle dado puede traducirse en el espacio siempre y cuando el origen permanezca dentro de él. Para dar cuenta de esto, multiplicamos por el área de un cuadrado de longitud lateral\(L/4\), que es el área máxima que puede ser encerrada por un bucle de perímetro\(L\). Por lo tanto, llegamos a la Ecuación\ ref {gupper}. Por último, observamos que el menor valor posible de\(L\) es\(L=4\), correspondiente a un cuadrado que encierra solo el sitio central. Por lo tanto

\[\sum_{\gamma\in\RUps\ns_{\!\Gamma}} e^{-2\beta J L\ns_{\gamma}} < {1\over 12} \sum_{k=2}^\infty k\cdot \big(3\,e^{-2\beta J}\big)^{2k} = {x^4 \, (2-x^2)\over 12\,(1-x^2)^2}\equiv r\ , \label{roft}\]

donde\(x=3\,e^{-2\beta J}\). Tenga en cuenta que hemos contabilizado el hecho de que el perímetro\(L\) de cada bucle\(\gamma\) debe ser un entero par. La suma es menor que la unidad proporcionada\(x < x\ns_0 = 0.869756 \ldots\), de ahí que el sistema se ordene siempre

\[{\kT\over J} < {2\over \ln(3/x\ns_0)}=1.61531\ .\]

El resultado exacto es\(\kB T\ns_\Rc=2J/\sinh^{-1}(1)=2.26918\ldots\) El argumento de Peierls también se ha generalizado a celosías de dimensiones superiores ².

Con un poco más de trabajo podemos derivar un límite para la magnetización. Hemos demostrado que

\[P\ns_-(0)={1\over Z}\sum_{\Gamma\in\RSigma\ns_+} e^{-2\beta J L\ns_\Gamma} \sum_{\gamma\in\RUps\ns_{\!\Gamma}} e^{-2\beta J L\ns_{\gamma}} < r\cdot {1\over Z}\sum_{\Gamma\in\RSigma\ns_+} e^{-2\beta J L\ns_\Gamma} = r\,P\ns_+(0)\ .\]

Por lo tanto,

\[1=P\ns_+(0)+P\ns_-(0) < (1+r) \, P\ns_+(0)\]

y por lo tanto

\[m = P\ns_+(0) - P\ns_-(0) > (1-r) \, P\ns_+(0) > {1-r\over 1+r}\ ,\]

donde\(r(T)\) se da en la Ecuación\ ref {roft}.

Figura\(\PageIndex{2}\): Una celosía cuadrada bidimensional mapeada sobre una cadena unidimensional.

¿Dos dimensiones o una?

Se demostró que el modelo unidimensional de Ising no tiene transición de fase de temperatura finita, y está desordenado a cualquier temperatura finita\(T\), pero en dos dimensiones en la celosía cuadrada hay una temperatura crítica finita\(T\ns_\Rc\) por debajo de la cual hay un orden de largo alcance. Consideremos ahora la construcción representada en la Figura \(\PageIndex{2}\), donde los sitios de una celosía cuadrada bidimensional se mapean sobre los de una cadena lineal ³. Claramente podemos obtener un mapeo uno a uno entre los sitios de una red cuadrada bidimensional y los de una cadena unidimensional. Es decir, el modelo bidimensional de celosía cuadrada Ising puede escribirse como un modelo unidimensional de Ising,

\[\HH=-J\!\!\sum_{\langle ij\rangle}^{\ssr{square}\atop\ssr{lattice}}\!\!\sigma\ns_i \, \sigma\ns_j = -\!\!\sum_{n,n'}^{\ssr{linear}\atop\ssr{chain}} \!\! J\ns_{nn'}\,\sigma\ns_n \, \sigma\ns_{n'}\ .\]

¿Cómo puede esto ser consistente con los resultados que acabamos de demostrar?

La mosca en la pomada aquí es que la interacción a lo largo de la cadena\(J\ns_{n,n'}\) es de largo alcance. Esto es evidente al inspeccionar las etiquetas del sitio en la Figura \(\PageIndex{2}\). Tenga en cuenta que\(n=15\) el sitio está vinculado a sitios\(n'=14\) y\(n'=16\), pero también a sitios\(n'=-6\) y\(n'=-28\). Con cada giro de las espirales concéntricas en la figura, el rango de la interacción aumenta. Para complicar aún más las cosas, las interacciones ya no son traduccionalmente invariantes,\(J\ns_{nn'}\ne J(n-n')\). Pero es la naturaleza a largo plazo de las interacciones en nuestra cadena unidimensional inventada la que estropea nuestro anterior argumento de entropía energética, porque ahora las paredes de dominio interactúan a través de un potencial de largo alcance. Considere por ejemplo la cadena lineal con\(J\ns_{n,n'}=J\,|n-n'|^{-\alpha}\), donde\(\alpha > 0\). Calculemos la energía de una configuración de muro de dominio donde\(\sigma\ns_n=+1\) si\(n > 0\) y\(\sigma\ns_n=-1\) si\(n\le 0\). La energía de la pared del dominio es entonces

\[\RDelta = \sum_{m=0}^\infty\sum_{n=1}^\infty {2J\over |m+n|^\alpha}\ .\]

Aquí hemos escrito una de las sumas en términos de\(m=-n'\). Para asintóticamente grandes\(m\) y\(n\), podemos escribir\(\BR=(m,n)\) y obtenemos una integral sobre el cuadrante superior derecho del plano:

\[\int\limits_1^\infty\!\!dR\> R\!\int\limits_0^{\pi/2}\!\!\!d\phi\>{2J\over R^\alpha \,(\cos\phi+\sin\phi)^\alpha}=2^{-\alpha/2}\!\!\!\! \int\limits_{-\pi/4}^{\pi/4}\!\!\!\!{d\phi\over\cos^\alpha\!\phi}\int\limits_1^\infty\!\!{dR\over R^{\alpha-1}}\ .\]

La\(\phi\) integral es convergente, pero la\(R\) integral diverge para\(\alpha\le 2\). Para un sistema finito, el límite superior de la\(R\) integral se convierte en el tamaño del sistema\(L\). Para\(\alpha>2\) el dominio la energía de la pared es finita en el límite termodinámico\(L\to\infty\). En este caso, la entropía vuelve a ganar. la entropía asociada a una sola pared de dominio es\(\kB\ln L\), y por lo tanto siempre\(F=E-\kT\) se baja al tener una densidad finita de paredes de dominio. Para\(\alpha<2\), la energía de un solo muro de dominio escala como\(L^{2-\alpha}\). Fue probado por primera vez por F. J. Dyson en 1969 que este modelo tiene una transición de fase de temperatura finita proporcionada\(1 < \alpha < 2\). No hay transición para\(\alpha<1\) o\(\alpha>2\). El caso\(\alpha=2\) es especial, y se discute como un caso especial en el hermoso análisis grupal de renormalización realizado por J. M. Kosterlitz en Phys. Rev. 37, 1577 (1976).

Expansión a altas temperaturas

Consideremos una vez más el modelo ferromagnético de Ising en campo cero\((H=0)\), pero en una celosía arbitraria. La función de partición es

\[Z=\Tra e^{\beta J \sum_{\langle ij\rangle}\sigma\ns_i\,\sigma\ns_j} =\big(\!\cosh\beta J\big)^{N\ns_\ssr{L}}\Tra\Bigg\{\prod_{\langle ij\rangle} \big(1 + x\,\sigma\ns_i\,\sigma\ns_j\big)\Bigg\}\ , \label{HTEZ}\]

donde\(x=\tanh\beta J\) y\(N\ns_\ssr{L}\) es el número de enlaces. Para celosías regulares,\(N\ns_\ssr{L}=\half z N\), donde\(N\) está el número de sitios de celosía y\(z\) es el número de coordinación de celosía, el número de vecinos más cercanos para cada sitio. Hemos utilizado

\[e^{\beta J\sigma\sigma'}=\cosh\beta J \cdot \Big\{ 1 + \sigma\sigma'\,\tanh\beta J\Big\}=\begin{cases} e^{+\beta J} & {if}\ \sigma\sigma'=+1 \\ e^{-\beta J} & {if}\ \sigma\sigma'=-1\ .\end{cases}\]

Ampliamos la Ecuación\ ref {HTEZ} en potencias de\(x\), resultando en una suma de\(2^{N\ns_\ssr{L}}\) términos, cada uno de los cuales puede ser representado gráficamente en términos de los llamados animales de celosía. Un animal de celosía es una disposición distinta (incluyendo reflexiones y rotaciones) de plaquetas adyacentes en una celosía. Para que el rastro no desaparezca, sólo se permiten tales configuraciones y sus composiciones. Esto se debe a que cada uno\(\sigma\ns_i\) para cada sitio dado\(i\) debe ocurrir un número par de veces para que un término dado en la suma no desaparezca. Para todos esos términos, el rastro es\(2^N\). Dejar\(\Gamma\) representar una colección de animales de celosía, y\(g\ns_\Gamma\) la multiplicidad de\(\Gamma\). Entonces

\[Z=2^N\big(\!\cosh\beta J\big)^{N\ns_\ssr{L}}\sum_\Gamma g\ns_\Gamma \,\big(\!\tanh\beta J\big)^{L\ns_\Gamma}\ ,\]

donde\(L\ns_\Gamma\) es el número total de sitios en el diagrama\(\Gamma\), y\(g\ns_\Gamma\) es la multiplicidad de\(\Gamma\). Ya que\(x\) desaparece como\(T\to\infty\), este procedimiento se conoce como la expansión a alta temperatura (HTE).

Figura\(\PageIndex{3}\): Diagramas HTE en la celosía cuadrada y sus multiplicidades.

Para la celosía cuadrada, la enumeración de todos los animales de celosía con hasta el orden ocho se da en la Figura\(\PageIndex{3}\). Para el diagrama representado como una sola plaqueta elemental, existen\(N\) posibles ubicaciones para el vértice inferior izquierdo. Para el animal\(2\times 1\) plaquette, uno tiene\(g=2N\), porque hay dos orientaciones inequivalentes así como\(N\) traducciones. Para dos cuadrados elementales disjuntos, uno tiene\(g=\half N(N-5)\), lo que surge de restar configuraciones\(5N\) 'ilegales' que involucran líneas dobles (¡recuerde que cada enlace en la suma de partición aparece solo una vez!) , que se muestra en la figura, y finalmente dividiendo por dos porque los cuadrados individuales son idénticos. Tenga en cuenta que siempre\(N(N-5)\) es par para cualquier valor entero de\(N\). Así, al orden más bajo interesante en la celosía cuadrada,

\[Z=2^N\big(\!\cosh\beta J\big)^{2N} \Big\{ 1 + Nx^4 + 2N x^6 + \big(7-\frac{5}{2}\big) N x^8 + \half N^2 x^8 + \CO(x^{10}) \Big\} \ .\]

La energía libre es por lo tanto

\[\begin{split} F&= -\kT\ln 2 + N\kT\ln(1-x^2) - N\kT \Big[ x^4 + 2\, x^6 + \frac{9}{2}\,x^8 + \CO(x^{10}) \Big]\\ &=N\kT\ln 2 - N\kT\Big\{ x^2 + \frac{3}{2}\, x^4 + \frac{7}{3}\, x^6 + \frac{19}{4}\,x^8 + \CO(x^{10})\Big\} , \end{split}\]

otra vez con\(x=\tanh\beta J\). Tenga en cuenta que hemos sustituido\(\cosh^2\!\beta J = 1/(1-x^2)\) para escribir el resultado final como una serie de potencia en\(x\). Observe que el\(\CO(N^2)\) factor in\(Z\) se ha cancelado al tomar el logaritmo, por lo que la energía libre es adecuadamente extensa.

Tenga en cuenta que la expansión a alta temperatura para la cadena unidimensional de Ising rinde

\[Z\ns_{chain}(T,N)=2^N\cosh^{N-1}\!\beta J \qquad,\qquad Z\ns_{ring}(T,N)=2^N\cosh^N\!\beta J\ ,\]

de acuerdo con los cálculos de la matriz de transferencia. En dimensiones superiores, donde hay una transición de fase de temperatura finita, normalmente se calcula el calor específico\(c(T)\) e intenta extraer su comportamiento singular en las proximidades de\(T\ns_\Rc\), donde\(c(T)\sim A\,(T-T\ns_\Rc)^{-\alpha}\). Ya que\(x(T)=\tanh(J/\kT)\) es analítico en\(T\), tenemos\(c(x)\sim A'\,(x-x\ns_\Rc)^{-\alpha}\), dónde\(x\ns_\Rc=x(T\ns_\Rc)\). Se asume que\(x\ns_\Rc\) es la singularidad más cercana al origen y corresponde al radio de convergencia de la expansión de alta temperatura. Si escribimos

\[c(x)=\sum_{n=0}^\infty a\ns_n\,x^n \sim A'' \bigg(1-{x\over x\ns_\Rc}\bigg)^{-\alpha}\ ,\]

entonces según el teorema binomial debemos esperar

\[{a\ns_n\over a\ns_{n-1}}={1\over x\ns_\Rc}\bigg[1-{1-\alpha\over n}\bigg]\ .\]

Así, al trazar\(a\ns_n/a\ns_{n-1}\) versus\(1/n\), se extrae\(1/x\ns_\Rc\) como la intercepción, y\((\alpha-1)/x\ns_\Rc\) como la pendiente.

Expansión a altas temperaturas para funciones de correlación

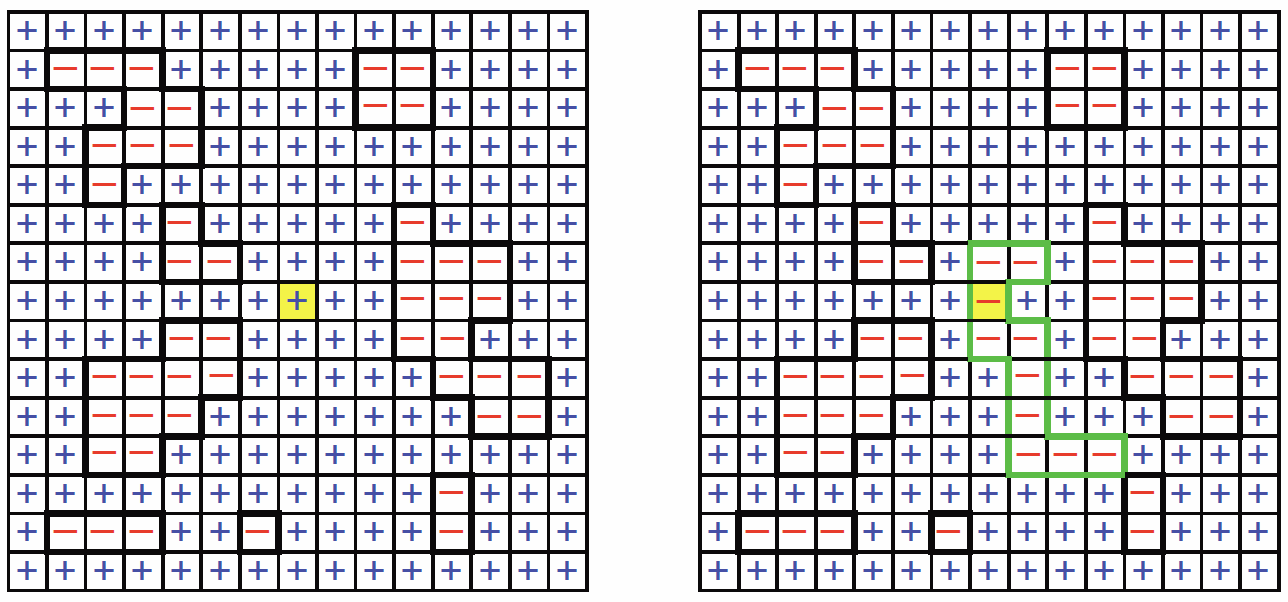
¿También podemos derivar una expansión de alta temperatura para la función de correlación spin-spin\(C\ns_{kl}=\langle \sigma\ns_k \, \sigma\ns_l \rangle\)? Sí podemos. Tenemos

\[C\ns_{kl}={\Tra\! \left[\sigma\ns_k\,\sigma\ns_l\,e^{\beta J \sum_{\langle ij\rangle}\sigma\ns_i\,\sigma\ns_j}\right] \over \Tra\! \left[e^{\beta J \sum_{\langle ij\rangle}\sigma\ns_i\,\sigma\ns_j}\right] } \equiv {Y\ns_{kl}\over Z}\ .\]

Recordemos nuestro análisis de la función de partición\(Z\). Concluimos que para que el rastro no desaparezca, la variable de giro\(\sigma\ns_i\) en cada sitio\(i\) debe ocurrir un número par de veces en la expansión del producto. Consideraciones similares se mantienen\(Y\ns_{kl}\), excepto ahora por la presencia de\(\sigma\ns_k\) y\(\sigma\ns_l\), esas variables ahora deben ocurrir un número impar de veces al expandir el producto. Es claro que los únicos diagramas que no se desvanecen serán aquellos en los que haya una cadena finita conectando sitios\(k\) y\(l\), además de los habituales bucles HTE cerrados. Ver Figura\(\PageIndex{4}\) para un boceto instructivo. Luego se expande tanto\(Y\ns_{kl}\) como\(Z\) en potencias de\(x=\tanh\beta J\), tomando la proporción para obtener el correlacionador\(C\ns_{kl}\). A altas temperaturas\((x\to 0)\), tanto el numerador como el denominador están dominados por las configuraciones\(\Gamma\) con el perímetro total más corto posible. Porque\(Z\), esto significa el camino trivial\(\Gamma=\{\emptyset\}\), mientras que para\(Y\ns_{kl}\) ello significa encontrar el camino de longitud más corta de\(k\) a\(l\). (Si no hay un camino en línea recta de\(k\) a\(l\), en general habrá varios de esos caminos de minimización). Obsérvese, sin embargo, que la presencia de la cadena entre sitios\(k\) y\(l\) complica el análisis de\(g\ns_\Gamma\) para los bucles cerrados, ya que ninguno de los enlaces de\(\Gamma\) puede intersectar la cadena. Cabe destacar que esto no significa que la cadena y los bucles cerrados no puedan cruzarse en sitios aislados, sino sólo que no comparten vínculos comunes; ver una vez más Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): Diagramas HTE para el numerador\(Y_{kl}\) de la función de correlación\(C_{kl}\). La ruta azul que conecta sitios\(k\) y\(l\) es la cadena. Los caminos rojos restantes son todos bucles cerrados.