6.2: Gases Clásicos Nonideal

Template:MathJaxArovas

Cambiemos de marcha ahora y volvamos al estudio de los sistemas clásicos continuos descritos por un hamiltoniano\(\HH\big(\{\Bx\ns_i\},\{\Bp\ns_i\}\big)\). En el siguiente capítulo, veremos cómo las propiedades críticas de los fluidos clásicos pueden modelarse de hecho mediante un modelo apropiado de Ising de gas reticular, y derivaremos métodos para describir la transición de fase líquido-gas en dicho modelo.

La Integral de Configuración

Considere la función de partición canónica ordinaria para un sistema no ideal de partículas puntuales idénticas que interactúan a través de un potencial central de dos cuerpos\(u(r)\). Trabajamos en el conjunto canónico ordinario. La función\(N\) de partición -particle es

\[\begin{split} Z(T,V,N)&={1\over N!}\!\int\!\prod_{i=1}^N {d^d\!p\ns_i\,d^d\!x\ns_i\over h^d}\> e^{-\HH/\kT}\\ &={\lambda_T^{-Nd}\over N!}\!\int\!\prod_{i=1}^Nd^d\!x\ns_i\>\exp\bigg(\!-{1\over\kT}\,\sum_{i<j}u\big(|\Bx\ns_i-\Bx\ns_j|\big)\bigg)\ . \end{split}\]

Aquí, hemos asumido un cuerpo muchos hamiltoniano de la forma

\[\HH=\sum_{i=1}^N {\Bp_i^2\over 2m} + \sum_{i<j}u\big(|\Bx\ns_i-\Bx\ns_j|\big)\ ,\]

en el que las partículas masivas no relativistas interactúan a través de un potencial central de dos cuerpos. Como antes,\(\lambda\ns_T=\sqrt{2\pi\hbar^2/m\kT\,}\) es la longitud de onda térmica. Ya podemos escribir

\[Z(T,V,N)=\lambda_T^{-Nd}\,Q\ns_N(T,V)\ ,\]

donde la integral de configuración\(Q\ns_N(T,V)\) viene dada por

\[Q\ns_N(T,V)={1\over N!}\int\!\!d^d\!x\nd_1\cdots\int\!\! d^d\!x\nd_N\,\prod_{i<j} e^{-\beta u(r\ns_{ij})}\ . \label{zconf}\]

No existen métodos generales para evaluar exactamente la integral configuracional.

Gas Tonks unidimensional

El gas Tonks es una generalización unidimensional del gas de esfera dura. Considerar un gas unidimensional de partículas indistinguibles de masa que\(m\) interactúan a través del potencial

\[u(x-x')=\begin{cases}\infty & \hbox{ if}\ |x-x'| < a \\ 0 & \hbox{ if}\ |x-x'| \ge a\ . \end{cases}\]

Así, el gas Tonks puede ser considerado como un gas de barras duras. El potencial anterior garantiza que la porción de espacio de configuración en la que se superponen las varillas está prohibida en este modelo ⁴. Dejar que el gas se coloque en un volumen finito\(L\). La naturaleza de esfera dura de las partículas significa que ninguna partícula puede llegar a una distancia\(\half a\) de los extremos en\(x=0\) y\(x=L\). Es decir, hay un potencial de un solo cuerpo\(v(x)\) actuando también, donde

\[v(x)=\begin{cases}\infty & \hbox{ if}\ x<\half a \\ 0 & \hbox{ if}\ \half a \le x \le L-\half a\\ \infty & \hbox{ if}\ x > L-\half a\ . \end{cases}\]

La integral de configuración del gas Tonks 1D viene dada por

\[Q\ns_N(T,L)={1\over N!}\int\limits_0^L\!dx\ns_1\cdots\int\limits_0^L\!dx\ns_N\> \xhi(x\ns_1,\ldots,x\ns_N)\ ,\]

donde\(\xhi = e^{-U/k\ns_\RB T}\) es cero si cualesquiera dos 'barras' (de longitud\(a\)) se superponen, o si alguna varilla se superpone con cualquiera de los límites en\(x=0\) y\(x=L\), y de\(\xhi=1\) otra manera. Tenga en cuenta que\(\xhi\) no depende de la temperatura. Sin pérdida de generalidad, podemos integrarnos sobre el subespacio donde\(x\ns_1 < x\ns_2 < \cdots < x\ns_N\) y luego multiplicar el resultado por\(N!\). Claramente\(x\ns_j\) debe mentir a la derecha\(x\ns_{j-1}+a\) y a la izquierda de\(Y\ns_j\equiv L - (N-j) a - \half a\). Así, la integral configuracional es

\[\begin{split} Q\ns_N(T,L)&=\!\!\int\limits_{a/2}^{Y\ns_1}\!\!dx\ns_1 \!\! \int\limits_{x\ns_1+a}^{Y\ns_2}\!\!\!\!dx\ns_2\> \cdots \!\!\!\!\!\!\! \int\limits_{x\ns_{N-1}+a}^{Y\ns_N} \!\!\!\!\!\!\! dx\ns_N\\ &=\!\!\int\limits_{a/2}^{Y\ns_1}\!\!dx\ns_1 \!\! \int\limits_{x\ns_1+a}^{Y\ns_2}\!\!\!\!dx\ns_2\> \cdots \!\!\!\!\!\!\! \int\limits_{x\ns_{N-2}+a}^{Y\ns_{N-1}} \!\!\!\!\!\!\! dx\ns_{N-1}\,\big( Y\ns_{N-1}-x\ns_{N-1}\big)\\ &=\!\!\int\limits_{a/2}^{Y\ns_1}\!\!dx\ns_1 \!\! \int\limits_{x\ns_1+a}^{Y\ns_2}\!\!\!\!dx\ns_2\> \cdots \!\!\!\!\!\!\! \int\limits_{x\ns_{N-3}+a}^{Y\ns_{N-2}} \!\!\!\!\!\!\! dx\ns_{N-2}\>\half\big( Y\ns_{N-2}-x\ns_{N-2}\big)^2=\cdots \\ &= {1\over N!}\>\big(X\ns_1-\half a\big)^N = {1\over N!}\>(L-Na)^N\ . \end{split}\]

La función de partición es\(Z(T,L,N)= \lambda_T^{-N}\,Q\ns_N(T,L)\), y así la energía libre es

\[F=-\kT\ln Z = -N\kT\Bigg\{-\ln\lambda\ns_T + 1 + \ln \bigg({L\over N}-a\bigg)\Bigg\}\ ,\]

donde hemos usado la regla de Stirling para escribir\(\ln N!\approx N\ln N - N\). La presión es

\[p=-{\pz F\over \pz L} = {\kT\over {L\over N} - a} = {n\kT\over 1-na}\ ,\]

donde\(n=N/L\) está la densidad unidimensional. Tenga en cuenta que la presión diverge a medida que\(n\) se acerca\(1/a\). La ley de gas ideal unidimensional habitual\(pL=N\kT\),, se sustituye por\(pL\ns_{ eff}=N\kT\), donde\(L\ns_{ eff}=L-Na\) está el volumen 'libre' obtenido restando el “volumen excluido” total\(Na\) del volumen original\(L\). Observe la similitud aquí con la ecuación de estado de van der Waals\((p+av^{-2})(v-b)=RT\),, donde\(v=\NA V / N\) está el volumen molar. Definiendo\({\tilde a}\equiv a/N_{\!\ssr{A}}^2\) y\({\tilde b}\equiv b/\NA\), tenemos

\[p+{\tilde a} n^2 = {n\kT\over 1-{\tilde b} n}\quad,\]

donde\(n=\NA/v\) está la densidad numérica. El término que involucra la constante\({\tilde a}\) se debe a la atracción de largo alcance de los átomos debido a su polarizabilidad mutua. El término implica\({\tilde b}\) es un efecto de volumen excluido. El gas Tonks modela solo este último.

Expansión de Cluster Mayer

Volvamos al problema general de computar la integral de configuración. Considera la función\(e^{-\beta u\ns_{ij}}\), donde\(u\ns_{ij}\equiv u(|\Bx\ns_i-\Bx\ns_j|)\). Suponemos que a distancias muy cortas hay una fuerte repulsión entre partículas,\(u\ns_{ij}\to\infty\) as\(r\ns_{ij}=|\Bx\ns_i-\Bx\ns_j|\to 0\), y eso\(u\ns_{ij}\to 0\) como\(r\ns_{ij}\to\infty\). Así, se\(e^{-\beta u\ns_{ij}}\) desvanece como\(r\ns_{ij}\to 0\) y se acerca a la unidad como\(r\ns_{ij}\to\infty\). Para nuestros fines, resultará útil definir la función

\[f(r)=e^{-\beta u(r)}-1\ ,\]

llamada la función Mayer después de Josef Mayer. Ahora podemos escribir

\[Q\ns_N(T,V)={1\over N!}\int\!\!d^d\!x\nd_1\cdots\int\!\! d^d\!x\nd_N\,\prod_{i<j} \big(1+f\nd_{ij}\big)\ . \label{zmany}\]

Figura\(\PageIndex{1}\): Panel inferior: Potencial de Lennard-Jones\(u(r)=4\eps \,\big(x^{-12}-x^{-6}\big)\), con\(x=r/\sigma\) y\(\eps=1\). Tenga en cuenta la débil cola atractiva y el fuerte núcleo repulsivo. Panel superior: Función Mayer\(f(r,T)=e^{-u(r)/k_{\ssr{B}}T}-1\) para\(k_{\ssr{B}}T=0.8\,\eps\) (azul),\(k_{\ssr{B}}T=1.5\,\eps\) (verde) y\(k_{\ssr{B}}T=5\,\eps\) (rojo).

Un potencial típico que podríamos considerar es el potencial semi-fenomenológico de Lennard-Jones,

\[u(r)=4\,\eps\,\bigg\{\Big({\sigma\over r}\Big)^{\!12}-\Big({\sigma\over r}\Big)^{\!6}\bigg\}\ .\]

Esto explica una atracción de larga distancia debido a fluctuaciones de dipolo eléctrico mutuamente inducidas, y una fuerte repulsión de corto alcance, fenomenológicamente modelada con un\(r^{-12}\) potencial, que imita un núcleo duro debido a la superposición de las distribuciones de electrones atómicos. Ajuste\(u'(r)=0\) obtenemos\(r^*=2^{1/6}\,\sigma\approx 1.12246\,\sigma\) al mínimo, donde\(u(r^*)=-\eps\). En contraste con el peso de Boltzmann\(e^{-\beta u(r)}\), la función Mayer\(f(r)\) desaparece como\(r\to\infty\), comportándose como\(f(r)\sim -\beta u(r)\). La función Mayer también depende de la temperatura. En la Figura se muestran bocetos de\(u(r)\) y\(f(r)\) para el modelo de Lennard-Jones\(\PageIndex{1}\).

El potencial ⁵ de Lennard-Jones es realista para ciertos fluidos simples, pero conduce a una configuración integral que en general es imposible de evaluar. De hecho, incluso un potencial tan simple como el del gas de esfera dura es intratable en más de una dimensión espacial. Sin embargo, podemos avanzar derivando una expansión en serie para la ecuación de estado en potencias de la densidad de partículas. Esto se conoce como la expansión virial. Como fue el caso cuando investigamos estadísticas cuánticas no interactuantes, es conveniente trabajar en el gran conjunto canónico y derivar expansiones de serie para la densidad\(n(T,z)\) y la presión\(p(T,z)\) en términos de fugacidad\(z\), luego resolver\(z(T,n)\) para obtener\(p(T,n)\). Estas expansiones en términos de fugacidad tienen una ingeniosa interpretación diagramática, debido a Mayer.

Comenzamos expandiendo el producto en la Ecuación\ ref {zmany} como

\[\prod_{i<j}\big(1+ f\ns_{ij}\big)=1+\sum_{i<j} f\ns_{ij} +\!\! \sum_{i<j\>,\>k<l\atop (ij)\ne(kl)} \!\! f\ns_{ij}\,f\ns_{kl} + \ldots\ .\]

Al existir\(\half N(N-1)\) posibles maridajes, hay\(2^{N(N-1)/2}\) términos en la expansión del producto anterior. Cada uno de estos términos puede ser representado por una gráfica, como se muestra en la Figura\(\PageIndex{2}\). Para cada uno de esos términos, trazamos una conexión entre puntos que representan diferentes partículas\(i\) y\(j\) si el factor\(f\nd_{ij}\) aparece en el término en consideración. La contribución para cualquier gráfica dada puede escribirse como un producto sobre las contribuciones de cada uno de sus clústeres de componentes desconectados. Por ejemplo, en el caso del término en Figura\(\PageIndex{2}\), la contribución a la integral configuracional sería

\[\begin{split} \RDelta Q &= {V^{N-11}\over N!}\int\!\!d^d\!x\nd_1\,d^d\!x\nd_4\,d^d\!x\nd_7\,d^d\!x\nd_9\ f\ns_{1,4}\,f\nd_{4,7}\,f\nd_{4,9}\,f\nd_{7,9}\\ &\hskip0.6in\times\int\!\!d^d\!x\nd_2\,d^d\!x\nd_5\,d^d\!x\nd_6\>f\nd_{2,5}\,f\nd_{2,6} \times\int\!\!d^d\!x\nd_3\,d^d\!x\nd_{10}\>f\nd_{3,10}\times\int\!\!d^d\!x\nd_8\,d^d\!x\nd_{11}\>f\nd_{8,11}\ . \end{split}\]

Nos referiremos a un producto dado de las funciones de Mayer que surge de esta expansión como término.

Figura\(\PageIndex{2}\): Diagrammatic interpretation of a term involving a product of eight Mayer functions.

Figura 6.6: Izquierda: John Lennard-Jones. Centro: Catherine Zeta-Jones. Derecha: James Earl Jones.

Las etiquetas particulares que asignamos a cada vértice de una gráfica dada no afectan el valor general de la gráfica. Ahora una gráfica dada sin etiquetar consiste en un cierto número de subgrafos conectados. Para un sistema con\(N\) partículas, entonces podemos escribir

\[N=\sum_\gamma m\nd_\gamma\,n\nd_\gamma\ ,\]

donde se\(\gamma\) extiende a lo largo de todos los subgráficos conectados posibles, y

\[\begin{aligned} m\ns_\gamma&=\hbox{ number of connected subgraphs of type $\gamma$ in the unlabeled graph}\\ n\ns_\gamma&=\hbox{ number of vertices in the connected subgraph $\gamma$}\ .\end{aligned}\]

Tenga en cuenta que el vértice único\(\bullet\) cuenta como un subgrafo conectado, con\(n\ns_\bullet=1\). Ahora nos preguntamos: ¿cuántas formas hay de asignar las\(N\) etiquetas a los\(N\) vértices de una gráfica dada sin etiquetar? Uno podría ser lo primero que la respuesta es simplemente\(N!\), sin embargo esto es demasiado grande, porque diferentes asignaciones de las etiquetas a los vértices pueden no resultar en una gráfica distinta. Para ver esto, considere los ejemplos en la Figura\(\PageIndex{3}\). En el primer ejemplo, una gráfica sin etiquetar con cuatro vértices consiste en dos subgrafías conectadas idénticas. Dada cualquier asignación de etiquetas a los vértices, entonces, podemos simplemente intercambiar los dos subgráficos y obtener el mismo término. Entonces debemos dividirnos\(N!\) por el producto\(\prod_\gamma m\ns_\gamma !\). Pero incluso esto no es suficiente, porque dentro de cada subgrafía conectada puede\(\gamma\) haber permutaciones que dejan inalterado al integrando, como se muestra en los ejemplos segundo y tercero de la Figura\(\PageIndex{3}\). Definimos el factor de simetría\(s\ns_\gamma\) como el número de permutaciones de las etiquetas que deja\(\gamma\) invariantes a una determinada subgrafía conectada. En la Figura se muestran ejemplos de factores de simetría\(\PageIndex{4}\). Considera, por ejemplo, el tercer subgrafo en la fila superior. Claramente se puede rotar la figura alrededor de su eje de simetría horizontal para obtener un nuevo etiquetado que representa el mismo término. Este doble eje es la única simetría que posee el diagrama, por lo tanto\(s\nd_\gamma=2\). Para el primer diagrama de la segunda fila, se puede rotar cualquiera de los triángulos alrededor del eje de simetría horizontal. También se puede rotar la figura e en el\(180^\circ\) plano para intercambiar los dos triángulos. Así, hay operaciones de\(2\times 2\times 2=8\) simetría que resultan en el mismo término, y\(s\nd_\gamma=8\). Por último, la última subgrafía de la segunda fila consta de cinco vértices cada uno de los cuales está conectado a los otros cuatro. Por lo tanto, cualquier permutación de las etiquetas da como resultado el mismo término, y\(s\nd_\gamma=5!=120\). Además de dividir por el producto\(\prod_\gamma m\nd_\gamma!\), entonces también debemos dividir por\(\prod_\gamma s_\gamma^{m\ns_\gamma}\).

Figura\(\PageIndex{3}\): Diferentes asignaciones de etiquetas a vértices pueden no resultar en un término distinto en la expansión de la integral de configuración.

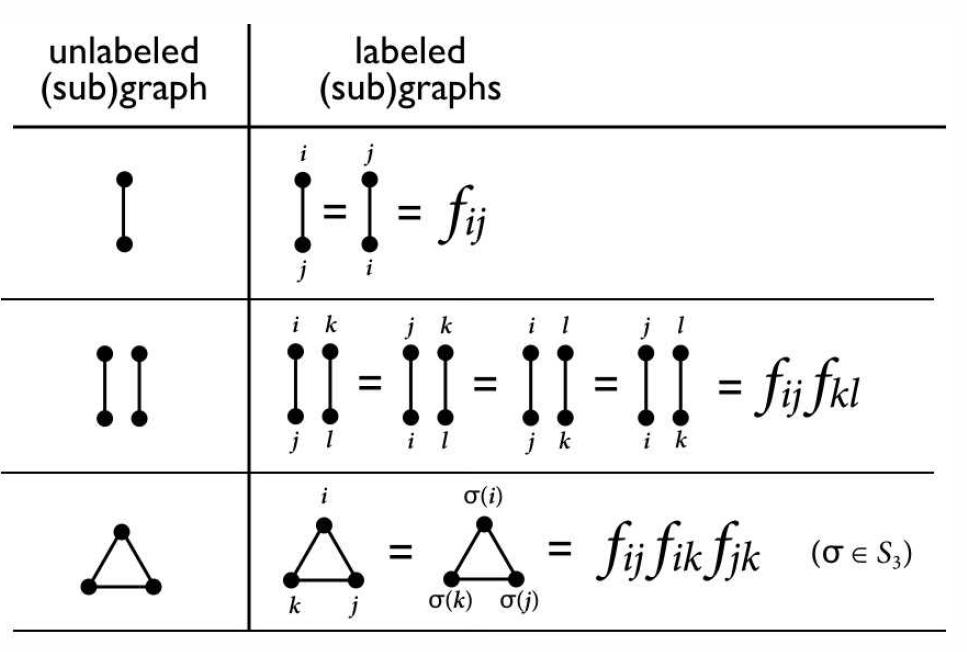
Ahora podemos escribir la función de partición como

\[\begin{split} Z&={\lambda_T^{-Nd}\over N!}\sum_{ \{m\ns_\gamma\}} {N!\over\prod m_\gamma!\>s_\gamma^{m\ns_\gamma} }\cdot\prod_\gamma \Bigg(\int\!\!d^d\!x\nd_1\cdots d^d\!x\nd_{n\ns_\gamma}\prod_{i<j}^\gamma f\nd_{ij}\Bigg)^{\!m\ns_\gamma}\!\cdot \delta\nd_{N\,,\,\sum m\ns_\gamma n\ns_\gamma}\\ &=\lambda_T^{-Nd}\sum_{ \{m\ns_\gamma\}}\prod_\gamma{\big(V b\ns_\gamma(T)\big)^{m\ns_\gamma}\over m\ns_\gamma!} \cdot\delta\nd_{N\,,\,\sum m\ns_\gamma n\ns_\gamma} \end{split}\]

donde el producto\(\prod_{i<j}^\gamma f\ns_{ij}\) está sobre todos los enlaces del subgrafo\(\gamma\). El delta final de Kronecker hace cumplir la restricción\(N=\sum_\gamma m\ns_\gamma\,n\ns_\gamma\). Hemos definido las integrales del clúster\(b\ns_\gamma\) como

\[b\ns_\gamma(T)\equiv {1\over s\ns_\gamma}\cdot{1\over V} \!\int\!\!d^d\!x\nd_1\cdots d^d\!x\nd_{n\ns_\gamma} \prod_{i<j}^\gamma f\nd_{ij}\quad,\]

donde asumimos el límite\(V\to\infty\). Ya que\(f\nd_{ij}=f\big(|\Bx\nd_i-\Bx\nd_j|\big)\), el producto\(\prod_{i<j}^\gamma f\nd_{ij}\) es invariante bajo traducción simultánea de todos los vectores de coordenadas por cualquier vector constante, y por lo tanto la integral sobre las variables de\(n\ns_\gamma\) posición contiene exactamente un factor del volumen, que se cancela con el prefactor en la definición anterior de \(b\ns_\gamma\). Así, cada integral de clúster es intensiva ⁶, escalando como\(V^0\).

Si calculamos la función grand partition, entonces la\(N\) restricción fija se relaja, y podemos hacer las sumas:

\[\begin{split} \Xi=e^{-\beta\Omega}&=\sum_{ \{m\ns_\gamma\} } \Big(e^{\beta\mu}\,\lambda_T^{-d}\Big)^{\sum m\ns_\gamma n\ns_\gamma} \prod_\gamma {1\over m\ns_\gamma !}\,\big(V \,b\ns_\gamma\big)^{m\ns_\gamma} \\ &=\prod_\gamma\sum_{m\ns_\gamma=0}^\infty {1\over m\ns_\gamma !}\>\Big(e^{\beta\mu}\, \lambda_T^{-d} \Big)^{m\ns_\gamma\,n\ns_\gamma}\big(V\,b\ns_\gamma\big)^{m\ns_\gamma}\\ &=\exp\bigg(V\sum_\gamma \big(e^{\beta\mu}\,\lambda_T^{-d}\big)^{n\ns_\gamma}\,b\ns_\gamma\bigg)\ . \end{split}\]

Por lo tanto,

\[\Omega(T,V,\mu)=-V\kT\,\sum_\gamma \big(e^{\beta\mu}\,\lambda_T^{-d}\big)^{n\ns_\gamma}\,b\ns_\gamma(T)\ ,\]

y podemos escribir

\[\begin{split} p&=\kT\sum_\gamma \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma(T)\\ n&=\sum_\gamma n\ns_\gamma\, \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma(T)\ , \label{pnofzT} \end{split}\]

donde\(z=\exp(\beta\mu)\) esta la fugacidad, y donde\(b\ns_\bullet\equiv 1\). Como en el caso de la mecánica estadística de gas cuántico ideal, podemos invertir sistemáticamente la relación\(n=n(z,T)\) a obtener\(z=z(n,T)\), y luego insertarla en la ecuación\(p(z,T)\) para obtener la ecuación de estado\(p=p(n,T)\). Esto arroja la expansión virial de la ecuación de estado,

\[p=n\kT\Big\{1+B\ns_2(T)\,n + B\ns_3(T)\,n^2 + \ldots\Big\}\ .\]

Figura\(\PageIndex{4}\): El factor de simetría\(s_\gamma\) para una subgráfica conectada\(\gamma\) es el número de permutaciones de sus índices lo que deja el término\(\prod_{(ij)\in\gamma}f_{ij}\) invariante.

Expansión de orden más baja

Tenemos

\[\begin{split} b\ns_-(T)&={1\over 2V}\int\!\!d^d\!x\ns_1\!\int\!\!d^d\!x\ns_2\>f\big(|\Bx\ns_1-\Bx\ns_2|\big)\\ &=\half\int\!\!d^d\!r\>f(r) \end{split}\]

y

\[\begin{split} b\ns_\wedge(T)&={1\over 2V}\int\!\!d^d\!x\ns_1\!\int\!\!d^d\!x\ns_2\>\!\int\!\!d^d\!x\ns_3\> f\big(|\Bx\ns_1-\Bx\ns_2|\big)\, f\big(|\Bx\ns_1-\Bx\ns_3|\big) \\ &=\half\int\!\!d^d\!r\!\int\!\!d^d\!r'\>f(r)\,f(r')=2\big(b\ns_-\big)^2 \end{split}\]

y

\[\begin{split} b\ns_\bigtriangleup(T)&={1\over 6V}\int\!\!d^d\!x\ns_1\!\int\!\!d^d\!x\ns_2\!\int\!\!d^d\!x\ns_3\> f\big(|\Bx\ns_1-\Bx\ns_2|\big) \> f\big(|\Bx\ns_1-\Bx\ns_3|\big)\> f\big(|\Bx\ns_2-\Bx\ns_3|\big)\\ &=\frac{1}{6}\int\!\!d^d\!r\!\int\!\!d^d\!r'\>f(r)\,f(r')\,f\big(|\Br-\Br'|\big)\ . \end{split}\]

Ahora podemos escribir

\[\begin{split} p&=\kT\Big\{ z\lambda_T^{-d} + \big(z\lambda_T^{-d} \big)^2\,b\ns_-(T) + \big(z\lambda_T^{-d} \big)^3\cdot\big(b\ns_\wedge + b\nd_\bigtriangleup\big)+\CO(z^4)\Big\}\\ n&=z\lambda_T^{-d} + 2\big(z\lambda_T^{-d} \big)^2\,b\ns_-(T) + 3\big(z\lambda_T^{-d} \big)^3\cdot\big(b\ns_\wedge + b\nd_\bigtriangleup\big)+\CO(z^4) \end{split}\]

Nosotros invertimos por escrito

\[z\lambda_T^{-d} =n + \alpha\ns_2\,n^2 + \alpha\ns_3\,n^3 + \ldots \label{zln}\]

y sustituyendo en la ecuación por\(n(z,T)\), rindiendo

\[n=(n + \alpha\ns_2\,n^2 + \alpha\ns_3\,n^3 ) + 2 (n+ \alpha\ns_2\,n^2 )^2\,b\ns_- + 3 n^3\, \big(b\ns_\wedge + b\nd_\bigtriangleup\big)+\CO(n^4)\ .\]

Por lo tanto,

\[0=(\alpha\ns_2+2 b\ns_-)\,n^2 + (\alpha\ns_3 + 4\alpha\ns_2\,b\ns_- + 3 b\ns_\wedge + 3 b\ns_\bigtriangleup)\,n^3 + \ldots\ .\]

Por lo tanto, concluimos

\[\begin{split} \alpha\ns_2&=-2b\ns_- \\ \alpha\ns_3&=-4\alpha\ns_2\,b\ns_- - 3b\ns_\wedge - 3 b\ns_\bigtriangleup\\ &=8 b^2_- - 6 b^2_- - 3 b\ns_\bigtriangleup=2 b^2_- -3 b\ns_\bigtriangleup\ . \end{split}\]

Ahora insertamos Ecuación\ ref {zln} con los valores determinados de\(\alpha\ns_{2,3}\) en la ecuación para\(p(z,T)\), obteniendo

\[\begin{split} {p\over\kT}&=n-2b\ns_-n^2 + (2b^2_- -3b\ns_\bigtriangleup)\,n^3+(n-2b\ns_- n^2)^2 \,b\ns_-+n^3\,(2b^2_- + b\ns_\bigtriangleup) + \CO(n^4)\\ &=n-b\ns_-\,n^2 - 2b\ns_\bigtriangleup\,n^3 + \CO(n^4)\ . \end{split}\]

Por lo tanto,

\[B\ns_2(T)=-b\ns_-(T)\qquad,\qquad B\ns_3(T)=-2 b\ns_\bigtriangleup(T)\ .\]

Tenga en cuenta que\(b\ns_\wedge\) no contribuye a\(B\ns_2\) — sólo\(\bigtriangleup\) aparece. Como veremos, esto se debe a que los coeficientes viriales\(B\ns_j\) involucran solo integrales de conglomerados\(b\ns_\gamma\) para cúmulos irreducibles de una partícula, aquellos conglomerados que permanecen conectados si se elimina alguno de los vértices más todos sus vínculos.

Cúmulos irreducibles de una partícula y expansión virial

Comenzamos con la Ecuación\ ref {PnOfZT} para\(p(T,z)\) y\(n(T,z)\),

\[\begin{split} p&=\kT\sum_\gamma \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma(T)\\ n&=\sum_\gamma n\ns_\gamma\, \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma(T)\ , \end{split}\]

donde\(b\ns_\gamma(T)\) para el clúster conectado\(\gamma\) viene dado por

\[b\ns_\gamma(T)\equiv {1\over s\ns_\gamma}\cdot{1\over V} \!\int\!\!d^d\!x\nd_1\cdots d^d\!x\nd_{n\ns_\gamma}\prod_{i<j}^\gamma f\nd_{ij}\ .\]

Es conveniente trabajar con cantidades adimensionales, usando\(\lambda_T^d\) como unidad de volumen. Para ello, definir

\[\nu\equiv n\lambda_T^d\qquad,\qquad\pi\equiv p\lambda_T^d \qquad,\qquad c\ns_\gamma(T)\equiv b\ns_\gamma(T)\,\big(\lambda_T^d\big)^{\!n\ns_\gamma -1}\ ,\]

para que

\[\beta\pi=\sum_\gamma c\ns_\gamma\, z^{n\ns_\gamma}=\sum_{\ell=1}^\infty d\ns_\ell\,z^\ell\qquad,\qquad \nu=\sum_\gamma n\ns_\gamma c\ns_\gamma\, z^{n\ns_\gamma}=\sum_{l=1}^\infty \ell\, d\ns_\ell\,z^\ell\ ,\]

donde

\[d\ns_\ell=\sum_\gamma c\ns_\gamma\,\delta\ns_{n\ns_\gamma\,,\,\ell}\]

es la suma de todos los clústeres conectados con\(\ell\) vértices. Aquí y en adelante, la dependencia funcional de\(T\) es implícita;\(\pi\) y\(\nu\) se consideran aquí como funciones explícitas de\(z\). Podemos, en principio, invertir para obtener\(z(\nu)\). Escribamos esta inversa como

\[z(\nu)=\nu\,\exp\!\bigg(\!-\sum_{k=1}^\infty \beta\ns_k\,\nu^k\bigg)\ .\]

En última instancia necesitamos obtener expresiones para los coeficientes\(\beta\ns_k\), pero vamos a asumir primero la forma anterior y utilizarla para escribir\(\pi\) en términos de\(\nu\). Tenemos

\[\begin{split} \beta\pi&=\sum_{\ell=1}^\infty d\ns_\ell\,z^\ell = \int\limits_0^z\!\! d{\tilde z}\,\sum_{l=1}^\infty \ell\, d\ns_\ell\,{\tilde z}^{\ell-1} =\int\limits_0^\nu\!\! d{\tilde\nu}\,{d{\tilde z}\over d{\tilde\nu}} \, {\tilde\nu} \over {\tilde z} = \int\limits_0^\nu\!\! d{\tilde\nu}\,{d\ln {\tilde z}\over d\ln {\tilde\nu}}\\ &=\int\limits_0^\nu\!\!d{\tilde\nu}\,\bigg(1-\sum_{k=1}^\infty k\,\beta\ns_k\,{\tilde\nu}^k\bigg) =\nu -\sum_{k=1}^\infty {k\,\beta\ns_k\over k+1}\,\nu^{k+1}\equiv\sum_{k=1}^\infty \CB\ns_k\,\nu^k\ , \end{split}\]

donde\(\CB\ns_k=B\ns_k\,\lambda_T^{-d(k-1)}\) está el coeficiente\(k^{ th}\) virial adimensional. Así,\(\CB\ns_{k=1}=1\) y

\[\CB\ns_k=-{k-1\over k}\,\beta\ns_{k-1}\]

para\(k>1\). También podemos obtener las integrales del clúster\(d\ns_\ell\) en términos de\(\beta\ns_k\). Para ello, tenga en cuenta que\(\ell^2d_\ell\) es el coeficiente de\(z^\ell\) en la función\(z\,d\nu/ dz\), de ahí

\[\begin{split} \ell^2 d\ns_\ell&=\oint {dz\over 2\pi i z}\,{1\over z^\ell}\bigg(z\,{d\nu\over dz}\bigg) = \oint {d\nu\over 2\pi i}\,z^{-\ell} =\oint {d\nu\over 2\pi i}\,{1\over\nu^\ell}\,\prod_{k=1}^\infty e^{\ell\beta\ns_k\nu^k}\\ &=\oint {d\nu\over 2\pi i}\,{1\over\nu^\ell}\,\sum_{\{m\ns_k\}}\prod_{k=1}^\infty {(\ell\,\beta\ns_k)^{m\ns_k}\over m\ns_k!}\,\nu^{k m\ns_k} =\sum_{\{m\ns_k\}}\delta\ns_{\sum_k k m\ns_k\,,\,\ell-1}\prod_{k=1}^\infty {(\ell\,\beta\ns_k)^{m\ns_k}\over m\ns_k!}\ . \end{split}\]

Clusters irreducibles

Los clusters a los que contribuyen\(d\ns_\ell\) están todos conectados, por definición. Sin embargo, es útil hacer una distinción adicional basada en la topología de clústeres conectados y definir un clúster conectado\(\gamma\) para que sea irreducible si, al eliminar cualquier sitio en\(\gamma\) y todos los enlaces conectados a ese sitio, los sitios restantes del clúster siguen conectado. La situación se representa en la Figura\(\PageIndex{5}\).

Figu re\(\PageIndex{5}\): Clústeres conectados versus irreducibles. Los clústeres (a) a (d) son irreducibles en el sentido de que permanecen conectados si se elimina algún sitio de componente y sus vínculos de conexión. El cluster (e) está conectado, pero es reducible. Su integral\(c_\gamma\) puede reducirse a un producto sobre sus componentes irreducibles, cada uno mostrado en un color único.

Para un cluster reducible\(\gamma\), la integral\(c\ns_\gamma\) es proporcional a un producto de integrales de cluster sobre sus componentes irreducibles. Definamos el conjunto\(\Gamma\ns_\ell\) como el conjunto de todos los racimos irreducibles de\(\ell\) vértices. Resulta que

\[\beta\ns_k(T)={1\over V\lambda_T^{(k-1)d}}{1\over k!}\!\sum_{\gamma\in \Gamma\ns_{k+1}}\!\! \int\!\!d^d\!x\ns_1\cdots\int\!\!d^d\!x\ns_k\prod_{\langle ij\rangle}^\gamma f\ns_{ij}\]

Así, los coeficientes viriales\(B\ns_j(T)\) se obtienen sumando un conjunto restringido de integrales de conglomerados, a saber.

\[B\ns_j(T)=-{k-1\over k}\,\beta\ns_{k-1}(T)\,\lambda_T^{(k-1)d}\quad.\]

Al final, ¡resulta que no necesitamos los factores de simetría en absoluto!

Receta de libro de cocina

¡Solo sigue estos sencillos pasos!

• La presión y la densidad numérica se escriben como una expansión sobre clústeres conectados sin etiquetar\(\gamma\), a saber.\[\begin{split} \beta p&=\sum_\gamma \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma\\ n&=\sum_\gamma n\ns_\gamma\, \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma\ . \end{split}\]
• Para cada término en cada una de estas sumas, dibuje el clúster conectado sin etiquetar\(\gamma\).
• Asignar etiquetas\(1\,,\,2\,,\,\ldots\,,\,n\ns_\gamma\) a los vértices, donde\(n\ns_\gamma\) está el número total de vértices en el clúster\(\gamma\). No importa cómo asignes las etiquetas.
• Anote el producto\(\prod_{i<j}^\gamma f\ns_{ij}\). El factor\(f\ns_{ij}\) aparece en el producto si hay un enlace en su clúster (ahora etiquetado) entre sitios\(i\) y\(j\).
• El factor de simetría\(s\ns_\gamma\) es el número de elementos del grupo simétrico\(S\ns_{n\ns_\gamma}\) que dejan el producto\(\prod_{i<j}^\gamma f\ns_{ij}\) invariante. La permutación de identidad deja el producto invariante, entonces\(s\ns_\gamma\ge 1\).
• La integral del clúster es\[b\ns_\gamma(T)\equiv {1\over s\ns_\gamma}\cdot{1\over V} \!\int\!\!d^d\!x\nd_1\cdots d^d\!x\nd_{n\ns_\gamma}\prod_{i<j}^\gamma f\nd_{ij}\ .\] Debido a la invarianza de la traducción,\(b\ns_\gamma(T)\propto V^0\). Por lo tanto\(\Bx\ns_{n\ns_\gamma}\equiv 0\), se puede establecer, eliminar el factor de volumen del denominador y realizar la integral sobre las\(n\ns_\gamma\!-\!1\) coordenadas restantes.
• Este procedimiento genera expansiones para\(p(T,z)\) y\(n(T,z)\) en poderes de la fugacidad\(z=e^{\beta\mu}\). Para obtener algo útil como\(p(T,n)\), invertimos la ecuación\(n=n(T,z)\) para encontrar\(z=z(T,n)\), y luego la sustituimos en la ecuación\(p=p(T,z)\) para obtener\(p=p\big(T,z(T,n)\big)=p(T,n)\). El resultado es la expansión virial,\[p=n\kT\,\Big\{1+B\ns_2(T)\,n + B\ns_3(T)\,n^2 + \ldots\Big\}\ ,\] donde\[B\ns_k(T)=-{1\over k (k-2)!}\sum_{\gamma\in \Gamma\ns_k} \int\!\!d^d\!x\ns_1\cdots\!\!\int\!\!d^d\!x\ns_{k-1}\prod_{\langle ij\rangle}^\gamma f\ns_{ij}\] con\(\Gamma\ns_k\) el conjunto de todos los racimos irreducibles de\(j\) sitio de una partícula.

Gas de esfera dura en tres dimensiones

El potencial de la esfera dura viene dado por

\[u(r)=\begin{cases} \infty & \hbox{ if $r\le a$} \\ 0 & \hbox{ if $r>a$\ .} \end{cases} \label{hspot}\]

Aquí\(a\) está el diámetro de las esferas. La función Mayer correspondiente es entonces independiente de la temperatura, y dada por

\[f(r)=\begin{cases}-1 & \hbox{ if $r\le a$} \\ 0 & \hbox{ if $r>a$\ .} \end{cases}\]

Podemos cambiar variables

\[b\ns_-(T)=\half\!\!\int\!\!d^3\!r\>f(r)=-\frac{2}{3}\pi a^3\ .\]

El cálculo de\(b\ns_\bigtriangleup\) es más desafiante. Tenemos

\[b\ns_\bigtriangleup=\frac{1}{6}\!\!\int\!\!d^3\!\rho\!\int\!\!d^3\!r\>f(\rho)\,f(r)\, f\big(|\Br-\Brho|\big)\ .\]

Primero debemos calcular el volumen de superposición para las esferas de radio\(a\) (la recuperación\(a\) es el diámetro de las partículas de esfera dura constitutivas) centradas en\(0\) y en\(\Brho\):

\[\begin{split} \CV&=\int\!\!d^3\!r\,f(r)\,f\big(|\Br-\Brho|\big)\\ \label{shaded} &=2\!\int\limits_{\rho/2}^a\!\!dz\>\pi(a^2-z^2)=\frac{4\pi }{3}a^3 - \pi a^2 \rho + \frac{\pi}{12}\,\rho^3\ . \end{split}\]

Luego nos integramos sobre la región\(|\Brho|<a\), para obtener

\[b\ns_\bigtriangleup=-\frac{1}{6}\cdot 4\pi\!\!\int\limits_0^a\!\!d\rho \> \rho^2\cdot \Big\{\frac{4\pi }{3}a^3 - \pi a^2 \rho + \frac{\pi}{12}\,\rho^3\Big\} =-\frac{5\pi^2}{36}\,a^6\ .\]

Por lo tanto,

\[p=n\kT\,\Big\{1+\frac{2\pi}{3}a^3 n + \frac{5\pi^2}{18} a^6 n^2 + \CO(n^3)\Big\}\ .\]

Figura\(\PageIndex{6}\): El solapamiento de las funciones de Mayer de esfera dura. El volumen sombreado es\(\CV\).

Cola débilmente atractiva

Supongamos

\[u(r)=\begin{cases} \infty & \hbox{ if $r\le a$} \\ -u\ns_0(r) & \hbox{ if $r>a$\ .} \end{cases}\]

Entonces la función Mayer correspondiente es

\[f(r)=\begin{cases}-1 & \hbox{ if $r\le a$} \\ e^{\beta u\ns_0(r)}-1 & \hbox{ if $r>a$\ .} \end{cases}\]

Por lo tanto,

\[b\ns_-(T)=\half\!\int\!\!d^3\!r\,f(r)=-\frac{2\pi}{3}a^3 + 2\pi\!\int\limits_a^\infty\!\!dr\,r^2\>\Big[e^{\beta u\ns_0(r)}-1\Big]\ .\]

Así, el segundo coeficiente virial es

\[B\ns_2(T)=-b\ns_-(T)\approx \frac{2\pi}{3}a^3 - {2\pi\over\kT}\!\int\limits_a^\infty\!\!dr\,r^2\,u\ns_0(r)\ ,\]

donde hemos asumido\(\kT\ll u\ns_0(r)\). Vemos que el segundo coeficiente virial cambia de signo a alguna temperatura\(T\ns_0\), de un valor negativo de baja temperatura a un valor positivo de alta temperatura.

Pozo Potencial Esférico

Considere un atractivo potencial de pozo esférico con un núcleo infinitamente repulsivo,

\[u(r)=\begin{cases} \infty & \hbox{ if $r\le a$} \\ -\eps & \hbox{ if $a<r<R$}\\ 0 & \hbox{ if $r>R$}\ . \end{cases}\]

Entonces la función Mayer correspondiente es

\[f(r)=\begin{cases}-1 & \hbox{ if $r\le a$} \\ e^{\beta \eps}-1 & \hbox{ if $a<r<R$}\\ 0 & \hbox{ if $r>R$}\ . \end{cases}\]

Redacción\(s\equiv R/a\), tenemos

\[\begin{split} B\ns_2(T)&=-b\ns_-(T)=-\half\!\int\!\!d^3\!r\,f(r)\\ &=-{1\over 2}\,\bigg\{ (-1)\cdot\frac{4\pi}{3}a^3 + \big(e^{\beta\eps}-1\big)\cdot\frac{4\pi}{3}a^3 (s^3-1)\bigg\}\\ &=\frac{2\pi}{3}a^3\,\bigg\{1-(s^3-1)\big(e^{\beta\eps}-1\big)\bigg\}\ . \end{split}\]

Para encontrar la temperatura\(T\ns_0\) donde se\(B\ns_2(T)\) indican los cambios, establecemos\(B\ns_2(T\ns_0)=0\) y obtenemos

\[\kB T\ns_0=\eps\bigg/\ln\!\bigg({s^3\over s^3-1}\bigg)\ .\]

Recordemos en nuestro estudio de la termodinámica del efecto Joule-Thompson en §1.10.6 que el proceso de estrangulamiento es isentálpico. El cambio de temperatura, cuando un gas es empujado (o escapa) a través de un tapón poroso de una región de alta presión a una de baja presión es

\[\RDelta T=\int\limits_{p\ns_1}^{p\ns_2}\!\!dp\,\pabc{T}{p}{H}\ ,\]

donde

\[\pabc{T}{p}{H}={1\over C\ns_p}\Bigg[ T\pabc{V}{T}{p}-V\Bigg]\ .\]

Apelando a la expansión virial, y trabajando al orden más bajo en correcciones a la ley de gas ideal, tenemos

\[p={N\over V}\,\kT + {N^2\over V^2}\,\kT\,B\ns_2(T)+\ldots\]

y calculamos\(\big(\frac{\pz V}{\pz T}\big)\nd_p\) configurando

\[0=dp=-{N\kT\over V^2}\,dV + {N\kB\over V}\,dT - {2N^2\over V^3}\,\kT\,B\ns_2(T)\,dV +{N^2\over V^2}\,d\big(\kT\,B\ns_2(T)\big) + \ldots\ .\]

Figura\(\PageIndex{7}\): Un pozo esférico atractivo con un núcleo repulsivo\(u(r)\) y su función Mayer asociada\(f(r)\).

Dividiendo por\(dT\), encontramos

\[T\pabc{V}{T}{p}-V=N\Bigg[ T\,{\pz B\ns_2\over\pz T} - B\ns_2\Bigg]\ .\]

La temperatura donde\(\big(\frac{\pz T}{\pz p}\big)\nd_H\) cambia signo se llama la temperatura de inversión\(T^*\). Para encontrar el punto de inversión, establecemos\(T^*\, B'_2(T^*)=B\ns_2(T^*)\),

\[{d\ln B\ns_2\over d\ln T}\bigg|\nd_{T^*}\!\!=1\ .\]

Si nos aproximamos\(B\ns_2(T)\approx A-{B\over T}\), entonces la temperatura de inversión sigue simplemente:

\[{B\over T^*}=A-{B\over T^*} \qquad\Longrightarrow\qquad T^*={2B\over A}\ .\]

Esferas duras con pared dura

Considera un gas esfera dura en tres dimensiones en presencia de una pared dura en\(z=0\). El gas está confinado a la región\(z>0\). La energía potencial total es ahora

\[W(\xoN)=\sum_i v(\Bx\ns_i) + \sum_{i<j} u(\Bx\ns_i-\Bx\ns_j)\ ,\]

donde

\[v(\Br)=v(z)=\begin{cases} \infty & { if}\quad z\le\half a \\ 0 & { if}\quad z > \half a\ , \end{cases}\]

y\(u(\Br)\) se da en la Ecuación\ ref {hspot}. El gran potencial está escrito como una serie en el número total de partículas\(N\), y viene dado por

\[\Xi=e^{-\beta\Omega} = 1+\xi\!\int\!\!d^3\!r\,e^{-\beta v(z)} + \half\xi^2\!\int\!\!d^3\!r\!\int\!\!d^3\!r'\>e^{-\beta v(z)}\,e^{-\beta v(z')}\, e^{-\beta u(\Br-\Br')} + \ldots\ ,\]

donde\(\xi=z\,\lambda_T^{-3}\), con\(z=e^{\mu/\kT}\) la fugacidad. Tomando el logaritmo, e invocando la serie Taylor\(\ln(1+\delta)=\delta-\half\delta^2 + \third\delta^3 - \ldots\), obtenemos

\[-\beta\Omega=\xi\!\!\!\int\limits_{z>{a\over 2}}\!\!\!\!d^3\!r + \half \xi^2\!\!\!\int\limits_{z>{a\over 2}}\!\!\!\!d^3\!r \!\!\!\int\limits_{z'>{a\over 2}}\!\!\!\!d^3\!r'\,\Big[ e^{-\beta u(\Br-\Br')}-1\Big]+ \ldots\]

El volumen es\(V\!=\!\!\!\int\limits_{z>0} \!\!\!d^3\!r\). Dividiendo por\(V\), tenemos, en el límite termodinámico,

\[\begin{split} -{\beta\Omega\over V}=\beta p&=\xi + \half \xi^2{1\over V}\!\!\!\int\limits_{z>{a\over 2}}\!\!\!\!d^3\!r \!\!\!\int\limits_{z'>{a\over 2}}\!\!\!\!d^3\!r'\,\Big[ e^{-\beta u(\Br-\Br')}-1\Big]+ \ldots\\ &=\xi-\frac{2}{3}\pi a^3\,\xi^2 + \CO(\xi^3)\ . \end{split}\]

La densidad numérica es

\[n=\xi\,{\pz\over\pz\xi}\,(\beta p)=\xi-\frac{4}{3}\pi a^3\,\xi^2 + \CO(\xi^3)\ ,\]

e invirtiendo para obtener\(\xi(n)\) y luego sustituyendo en la ecuación de presión, obtenemos la expansión virial de orden más bajo para la ecuación de estado,

\[p=\kT\,\Big\{n + \frac{2}{3}\pi a^3\,n^2 + \ldots\Big\}\ .\]

Como era de esperar, la presencia del muro no afecta a una propiedad a granel como la ecuación de estado.

Figura\(\PageIndex{8}\): Ante la presencia de una pared dura, la esfera de Mayer se corta en el lado más cercano a la pared. La densidad resultante se\(n(z)\) desvanece\(z<\half a\) ya que el centro de cada esfera debe estar al menos a un radio de\((\half a)\) distancia de la pared. Entre\(z=\half a\) y\(z=\frac{3}{2} a\) hay una mejora de densidad. Si el cálculo se llevara a cabo en orden superior,\(n(z)\) exhibiría oscilaciones espaciales amortiguadas con longitud de onda\(\lambda\sim a\).

A continuación, calculemos la densidad numérica\(n(z)\), dada por

\[n(z)=\blangle\,\sum_i\delta(\Br-\Br\ns_i)\>\brangle\ .\]

Debido a la invarianza traslacional en el\((x,y)\) plano, sabemos que la densidad debe ser una función de\(z\) solo. La presencia del muro en las\(z=0\) rupturas de la simetría traslacional en la\(z\) dirección. La densidad numérica es

\[\begin{split} n(z)&={ Tr} \bigg[e^{\beta(\mu\HN-\HH)}\,\sum_{i=1}^N\delta(\Br-\Br\ns_i)\bigg]\bigg/{ Tr}\ e^{\beta(\mu\HN-\HH)}\\ &=\Xi^{-1}\>\Bigg\{\xi\,e^{-\beta v(z)} + \xi^2\,e^{-\beta v(z)}\!\int\!\!d^3\!r'\,e^{-\beta v(z')}\,e^{-\beta u(\Br-\Br')} \, +\ \ldots\Bigg\}\\ &=\xi\,e^{-\beta v(z)} + \xi^2\,e^{-\beta v(z)}\!\int\!\!d^3\!r'\,e^{-\beta v(z')}\,\Big[e^{-\beta u(\Br-\Br')}-1\Big] \, +\ \ldots\ . \end{split}\]

Tenga en cuenta que el término entre corchetes en la última línea es la función Mayer\(f(\Br-\Br')=e^{-\beta u(\Br-\Br')}-1\). Considera la función

\[e^{-\beta v(z)}\,e^{-\beta v(z')}\,f(\Br-\Br')=\begin{cases} 0 & \hbox{ if $z<\half a$ or $z'<\half a$}\\ 0 & \hbox{ if $|\Br-\Br'|>a$}\\ -1 & \hbox{ if $z>\half a$ and $z'>\half a$ and $|\Br-\Br'|<a$}\ . \end{cases}\]

Consideremos ahora la integral de la función anterior con respecto a\(\Br'\). Claramente el resultado depende del valor de\(z\). Si\(z>\frac{3}{2}a\), entonces no hay región excluida en\(\Br'\) y la integral es\((-1)\) veces el volumen completo de la esfera Mayer,\(-\frac{4}{3}\pi a^3\). Si\(z<\half a\) la integral se desvanece por el\(e^{-\beta v(z)}\) factor. Para\(z\) infinitesimalmente mayor que\(\half a\), la integral es\((-1)\) veces la mitad del volumen de la esfera de Mayer,\(-\frac{2}{3}\pi a^3\). Para\(z\in\big[\frac{a}{2}\,,\,\frac{3a}{2}\big]\) la integral interpola entre\(-\frac{2}{3}\pi a^3\) y\(-\frac{4}{3}\pi a^3\). De manera explícita, se encuentra por integración elemental,

\[\int\!\!d^3\!r'\>e^{-\beta v(z)}\,e^{-\beta v(z')}\,f(\Br-\Br')=\begin{cases} 0 & \hbox{ if $z<\half a$}\\ \left[ -1-\frac{3}{2} \big({z\over a}-\half\big) + \half \big({z\over a}-\half\big)^3 \right]\cdot\frac{2}{3}\pi a^3& \hbox{ if $\half a < z < \frac{3}{2} a$}\\ -{4\over 3}\pi a^3 & \hbox{ if $z>\frac{3}{2}a$}\ . \end{cases}\]

Después de sustituir\(\xi=n+\frac{4}{3}\pi a^3 n^2 + \CO(n^3)\) para\(\xi\) relacionarse con la densidad aparente\(n=n\ns_\infty\), obtenemos el resultado deseado:

\[n(z)=\begin{cases} 0 & \hbox{ if $z<\half a$}\\ n+\left[ 1 -\frac{3}{2} \big({z\over a}-\half\big) + \half \big({z\over a}-\half\big)^3 \right]\cdot\frac{2}{3}\pi a^3\,n^2 & \hbox{ if $\half a < z < \frac{3}{2} a$}\\ n & \hbox{ if $z>\frac{3}{2}a$}\ . \end{cases}\]

Se proporciona un boceto en el panel derecho de la Figura\(\PageIndex{8}\). \(n(z)\)Obsérvese que la densidad desaparece de manera idéntica\(z<\half\) debido a la exclusión de las esferas duras por la pared. Para\(z\) entre\(\half a\) y\(\frac{3}{2} a\), hay una mejora de densidad, cuyo origen tiene una interpretación física simple. Dado que la pared excluye partículas de la región\(z<\half\), hay una losa vacía de espesor que\(\half z\) recubre el interior de la pared. Entonces no hay partículas en esta región que excluyan a los vecinos a su derecha, de ahí que la densidad se acumule justo al otro lado de esta losa. El efecto se desvanece al orden del cálculo pasado\(z=\frac{3}{2}a\), donde\(n(z)=n\) vuelve a su valor a granel. Si hubiéramos calculado en orden superior, habríamos encontrado oscilaciones amortiguadas con periodo espacial\(\lambda\sim a\).