6.4: Física del Estado Líquido

Template:MathJaxArovas

La función de distribución de múltiples partículas

La expansión virial se aplica típicamente a sistemas de baja densidad. Cuando la densidad es alta, cuando\(na^3\sim 1\), donde\(a\) es una escala típica de longitud molecular o atómica, la expansión virial es poco práctica. Hay muchos términos para calcular, y para avanzar hay que utilizar técnicas sofisticadas de reanudación para investigar el régimen de alta densidad.

Para dilucidar la física de los líquidos, es útil considerar las propiedades de diversas funciones de correlación. Estos objetos se derivan de la distribución\(N\) general de Boltzmann,

\[f(\Bx\nd_1,\ldots,\Bx\nd_N;\Bp\nd_1,\ldots,\Bp\nd_N)=\begin{cases} Z_N^{-1}\cdot{1\over N!}\,e^{-\beta\HH\ns_{\!N}(\Bp,\Bx)}&{OCE} \\ &\\ \Xi^{-1}\cdot {1\over N!}\,e^{\beta\mu N}\,e^{-\beta\HH\ns_{\!N}(\Bp,\Bx)} & {GCE}\ . \end{cases}\]

Asumimos un hamiltoniano de la forma

\[\HH\ns_{\!N}=\sum_{i=1}^N {\Bp_i^2\over 2m} + W(\xoN).\]

La cantidad

\[f(\Bx\nd_1,\ldots,\Bx\nd_N;\Bp\nd_1,\ldots,\Bp\nd_N)\,{d^d\!x\ns_1\,d^d\!p\ns_1\over h^d}\cdots{d^d\!x\ns_N\,d^d\!p\ns_N\over h^d}\]

es la capacidad de encontrar\(N\) partículas en el sistema, con la partícula #1 mintiendo dentro\(d^3\!x\ns_1\) de\(\Bx\ns_1\) y teniendo impulso dentro\(d^d\!p\ns_1\) de\(\Bp\nd_1\), Si calculamos promedios de cantidades que solo dependen de las posiciones\(\{\Bx\ns_j\}\) y no del momento\(\{\Bp\ns_j\}\), entonces podemos integrar el momenta para obtener, en la OCE,

\[P(\Bx\ns_1,\ldots,\Bx\ns_N)=Q_N^{-1}\cdot{1\over N!}\>e^{-\beta W(\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N)}\ ,\]

donde\(W\) está la energía potencial total,

\[W(\Bx\ns_1,\ldots,\Bx\ns_N)=\sum_i v(\Bx\ns_i)+\sum_{i<j} u(\Bx\ns_i-\Bx\ns_j) + \sum_{i<j<k} w(\Bx\ns_i-\Bx\ns_j\,,\,\Bx\ns_j-\Bx\ns_k)+ \ldots\ ,\]

y\(Q\ns_N\) es la configuración integral,

\[Q\ns_N(T,V)={1\over N!}\int\!\!d^d\!x\ns_1\cdots\int\!\! d^d\!x\ns_N\>e^{-\beta W(\xoN)}\ .\]

Nosotros, en su mayor parte, consideraremos solo como contribuyentes potenciales centrales de dos cuerpos\(W\), es decir, solo conservaremos el término medio en el RHS. Tenga en cuenta que\(P(\Bx\ns_1,\ldots,\Bx\ns_N)\) es invariante bajo cualquier permutación de las etiquetas de partículas.

Promedios sobre la Distribución

Para calcular un promedio, uno se integra sobre la distribución:

\[\blangle F(\Bx\ns_1,\ldots,\Bx\ns_N) \brangle=\int\!\!d^d\!x\ns_1\cdots\!\int\!\!d^d\!x\ns_N\>P(\xoN)\,F(\xoN)\ .\]

La densidad general\(N\) de probabilidad de partículas se normaliza de acuerdo con

\[\int\!\!d^d\!x\ns_N\>P(\Bx\ns_1,\ldots,\Bx\ns_N)=1\ .\]

La densidad local promedio es

\[\begin{split} n\ns_1(\Br)&= \blangle \sum_i\delta(\Br-\Bx\ns_i) \brangle \\ &=N\!\int\!\!d^d\!x\ns_2\cdots\!\int\!\!d^d\!x\ns_N\> P(\Br,\Bx\ns_2,\ldots,\Bx\ns_N)\ . \end{split}\]

Tenga en cuenta que la densidad local obedece a la regla de suma

\[\int\!\!d^d\!r\>n\ns_1(\Br)=N\ .\]

En un sistema traslacionalmente invariante,\(n\ns_1=n=\frac{N}{V}\) es una constante independiente de la posición. Los límites de un sistema romperán en general la invarianza traslacional, por lo que para mantener la noción de un sistema traduccionalmente invariante de volumen total finito, se deben imponer condiciones de límite periódicas.

La matriz de densidad de dos partículas\(n\ns_2(\Br\ns_1,\Br\ns_2)\) se define por

\[\begin{split} n\ns_2(\Br\ns_1,\Br\ns_2)&=\blangle\sum_{i\ne j} \delta(\Br\nd_1-\Bx\ns_i)\,\delta(\Br\ns_2-\Bx\ns_j) \brangle \\ &=N(N-1)\!\int\!\!d^d\!x\ns_3\cdots\!\int\!\!d^d\!x\ns_N\> P(\Br\ns_1,\Br\ns_2,\Bx\ns_3,\ldots,\Bx\ns_N)\ . \end{split}\]

Como en el caso de la matriz de densidad de una partícula, la densidad local\(n\ns_1(\Br)\), la matriz de densidad de dos partículas satisface una regla de suma:

\[\int\!\!d^d\!r\ns_1\!\int\!\!d^d\!r\ns_2\,n\ns_2(\Br\ns_1,\Br\ns_2)=N(N-1)\ .\]

Generalizando más, se define la matriz \(k\)de densidad de partículas como

\[\begin{split} n\ns_k(\Br\ns_1,\ldots,\Br\ns_k)&=\blangle{\sum_{i\ns_1\cdots i\ns_k}\!}' \delta(\Br\nd_1-\Bx\ns_{i\ns_1})\cdots\delta(\Br\ns_k-\Bx\ns_{i\ns_k})\ \brangle \\ &={N!\over (N-k)!}\!\int\!\!d^d\!x\ns_{k+1}\cdots\!\int\!\!d^d\!x\ns_N\> P(\Br\ns_1,\ldots,\Br\ns_k,\Bx\ns_{k+1},\ldots,\Bx\ns_N)\ , \end{split}\]

donde el primo en la suma indica que todos los índices\(i\ns_1,\ldots,i\ns_k\) son distintos. La regla de suma correspondiente es entonces

\[\int\!\!d^d\!r\ns_1\cdots\!\int\!\!d^d\!r\ns_k\,n\ns_k(\Br\ns_1,\ldots,\Br\ns_k)={N!\over (N-k)!}\ .\]

La energía potencial promedio se puede expresar en términos de las funciones de distribución. Asumiendo solo interacciones de dos cuerpos, tenemos

\[\begin{split} \langle W\rangle &=\blangle\sum_{i<j} u(\Bx\ns_i-\Bx\ns_j)\brangle\\ &=\half\!\int\!\!d^d\!r\ns_1\!\int\!\!d^d\!r\ns_2\>u(\Br\ns_1-\Br\ns_2)\> \blangle\sum_{i\ne j}\delta(\Br\ns_1-\Bx\ns_i)\,\delta(\Br\ns_2-\Bx\ns_j)\brangle\\ &=\half\!\int\!\!d^d\!r\ns_1\!\int\!\!d^d\!r\ns_2\>u(\Br\ns_1-\Br\ns_2)\,n\ns_2(\Br\ns_1,\Br\ns_2)\ . \end{split}\]

A medida que las separaciones se\(r\ns_{ij}=|\Br\ns_i-\Br\ns_j|\) hacen grandes, esperamos que las correlaciones desaparezcan, en cuyo caso

\[\begin{split} n\ns_k(\Br\ns_1,\ldots,\Br\ns_k)&=\blangle{\sum_{i\ns_1\cdots i\ns_k}\!}' \delta(\Br\nd_1-\Bx\ns_{i\ns_1})\cdots\delta(\Br\ns_k-\Bx\ns_{i\ns_k})\brangle\\ &\xrightarrow{ r\ns_{ij}\to\infty}{\sum_{i\ns_1\cdots i\ns_k}\!}' \blangle \delta(\Br\nd_1-\Bx\ns_{i\ns_1})\brangle \cdots\blangle\delta(\Br\ns_k-\Bx\ns_{i\ns_k}) \brangle\\ &={N!\over (N-k)!}\cdot{1\over N^k}\ n\ns_1(\Br\ns_1)\cdots n\ns_1(\Br\ns_k)\bvph\\ &=\bigg(1-{1\over N}\bigg)\bigg(1-{2\over N}\bigg)\cdots\bigg(1-{k-1\over N}\bigg)\,n\ns_1(\Br\ns_1)\cdots n\ns_1(\Br\ns_k)\ . \end{split}\]

La función \(k\)de distribución de partículas se define como la relación

\[g\ns_k(\Br\ns_1,\ldots,\Br\ns_k)\equiv {n\ns_k(\Br\ns_1,\ldots,\Br\ns_k)\over n\ns_1(\Br\ns_1)\cdots n\ns_1(\Br\ns_k)}\ .\]

Para grandes separaciones, entonces,

\[g\ns_k(\Br\ns_1,\ldots,\Br\ns_k) \xrightarrow { r\ns_{ij}\to\infty} \prod_{j=1}^{k-1}\bigg(1-{j\over N}\bigg)\ .\]

Para los sistemas isotrópicos, la función de distribución de dos partículas\(g\ns_2(\Br\ns_1,\Br\ns_2)\) depende únicamente de la magnitud\(|\Br\ns_1-\Br\ns_2|\). En función de esta separación escalar, la función se conoce como la función de distribución radial:

\[\begin{split} g(r)\equiv g\ns_2(\Br)&={1\over n^2}\>\blangle\sum_{i\ne j}\delta(\Br-\Bx\ns_i)\,\delta(\Bx\ns_j)\brangle\\ &={1\over Vn^2}\>\blangle \sum_{i\ne j}\delta(\Br-\Bx\ns_i+\Bx\ns_j)\brangle\ . \end{split}\]

La función de distribución radial es de gran importancia en la física de los líquidos porque

• propiedades termodinámicas del sistema pueden estar relacionadas con\(g(r)\)
• \(g(r)\)se puede medir directamente mediante experimentos de dispersión

Por ejemplo, en un sistema isotrópico la energía potencial promedio viene dada por

\[\begin{split} \langle W\rangle&=\half\!\int\!\!d^d\!r\ns_1\!\int\!\!d^d\!r\ns_2\>u(\Br\ns_1-\Br\ns_2)\,n\ns_2(\Br\ns_1,\Br\ns_2)\\ &=\half n^2\!\int\!\!d^d\!r\ns_1\!\int\!\!d^d\!r\ns_2\>u(\Br\ns_1-\Br\ns_2)\,g\big(|\Br\ns_1-\Br\ns_2|\big)\\ &={N^2\over 2V}\!\int\!d^d\!r\>u(r)\,g(r)\ . \end{split}\]

Para un sistema tridimensional, la energía interna (potencial) promedio por partícula es

\[{\langle W\rangle\over N}=2\pi n\!\int\limits_0^\infty\!\!dr\>r^2\,g(r)\,u(r)\ .\label{Wper}\]

Intuitivamente,\(f(r)\,dr\equiv 4\pi r^2\,n\,g(r)\,dr\) es el número promedio de partículas que se encuentran a una distancia radial entre\(r\) y\(r+dr\) desde una partícula de referencia dada. La energía potencial total de interacción con la partícula de referencia es entonces\(f(r)\,u(r)\,dr\). Ahora integre sobre todo\(r\) y divídalo por dos para evitar el doble conteo. Esto recupera la Ecuación\ ref {Wper}.

Figura Funciones de distribución de\(\PageIndex{1}\): pares para esferas duras de diámetro\(a\) en la fracción de llenado\(\eta=\frac{\pi}{6}a^3 n=0.49\) (izquierda) y para Argón líquido a\(T=85\,\) K (derecha). Los datos de dinámica molecular para esferas duras (puntos) se comparan con el resultado de la aproximación Percus-Yevick (ver más abajo en § 5.8). Reproducido (sin permiso) de J.-P. Hansen e I. R. McDonald, Teoría de los Líquidos Simples, fig 5.5. Los datos experimentales sobre argón líquido provienen del trabajo de dispersión de neutrones de J. L. Yarnell, Phys. Rev. A 7, 2130 (1973). Los datos (puntos) se comparan con los cálculos de dinámica molecular de Verlet (1967) para un fluido Lennard-Jones.

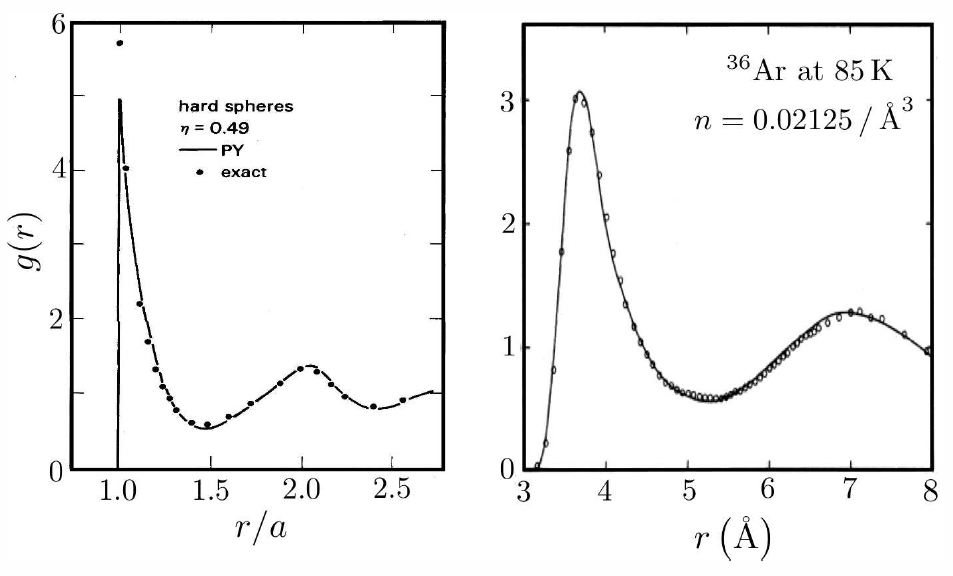
En la OCE,\(g(r)\) obedece la regla de la suma

\[\int\!\!d^d\!r\,g(r)={V\over N^2}\cdot N(N-1)=V-{V\over N}\ ,\]

de ahí

\[n\!\int\!\!d^d\!r\,\big[ g(r)-1\big]=-1\qquad \hbox{(OCE)}\ . \label{CSROCE}\]

La función\(h(r)\equiv g(r)-1\) se llama función de correlación de pares.

En la gran formulación canónica, tenemos

\[\begin{split} n\!\!\int\!\!d^3\!r\,h(r)&={\blangle N\brangle\over V}\cdot\Bigg[ {\blangle N(N-1)\brangle \over \langle N\rangle^2}\,V -V \Bigg]\\ &={\blangle N^2\brangle - \blangle N \brangle^{\!2}\over \blangle N \brangle} - 1 \bvph\\ &=n\kT\kappa\ns_T - 1\qquad \hbox{(GCE)}\ , \end{split}\label{CSRGCE}\]

donde\(\kappa\ns_T\) está la compresibilidad isotérmica. Tenga en cuenta que en un gas ideal tenemos\(h(r)=0\) y\(\kappa\ns_T=\kappa^0_T\equiv 1/n\kT\). Los sistemas autocondensados, como los líquidos y los sólidos lejos de la criticidad, son casi incompresibles, por lo tanto\(0 < n\kT\,\kappa\ns_T \ll 1\), y por lo tanto\(n\!\int\!d^3\!r\,h(r)\approx -1\). Para sistemas incompresibles, donde\(\kappa\ns_T=0\), esto se convierte en una igualdad.

Como veremos más adelante en § 5.4, la función\(h(r)\), o más bien su transformada de Fourier\(\Hh(\Bk)\), se mide directamente en un experimento de dispersión. Entonces surge la pregunta sobre qué resultado se aplica: el resultado OCE de la Ecuación\ ref {CSROCE} o el resultado GCE de la Ecuación\ ref {CSRGCE}. La respuesta es que bajo casi todas las condiciones experimentales es el resultado de GCE el que aplica. La razón de esto es que el experimento de dispersión normalmente ilumina solo un subconjunto de todo el sistema. Este subsistema se encuentra en equilibrio de partículas con el resto del sistema, de ahí que sea apropiado utilizar el gran conjunto canónico. Los resultados de OCE solo se aplicarían si el experimento de dispersión fuera para medir todo el sistema.

Figura\(\PageIndex{2}\): Funciones de distribución de par Monte Carlo para agua líquida. De A. K. Soper, Chem Phys. 202, 295 (1996).

Ecuación Virial de Estado

El virio de un sistema mecánico se define como

\[G=\sum_i\Bx\nd_i\cdot\BF\nd_i\ ,\]

donde\(\BF\ns_i\) es la fuerza total que actúa sobre la partícula\(i\). Si promediamos\(G\) a lo largo del tiempo, obtenemos

\[\begin{split} \langle G\rangle &=\lim_{T\to\infty} {1\over T}\!\int\limits_0^T\!\!dt\>\sum_i\Bx\nd_i\cdot\BF\nd_i\\ &=-\lim_{T\to\infty} {1\over T}\!\int\limits_0^T\!\!dt\>\sum_i m\,{\dot\Bx}_i^2\\ &=-3N\kT\ . \end{split}\]

Aquí, hemos hecho uso de

\[\Bx\ns_i\cdot\BF\ns_i=m\,\Bx\ns_i\cdot{\ddot\Bx}\ns_i=-\,m\,{\dot\Bx}_i^2+{d\over dt}\Big(m\,\Bx\ns_i\cdot{\dot\Bx}\ns_i\Big)\ ,\]

así como ergodicidad y equipartición de energía cinética. También hemos asumido tres dimensiones espaciales. En un sistema acotado, hay dos aportes a la fuerza\(\BF\ns_i\). Una contribución es de las superficies que encierran el sistema. Esto viene dado por ⁹

\[\langle G\rangle\nd_{surfaces}=\blangle\sum_i\Bx\ns_i\cdot\BF^{(surf)}_i\brangle = -3pV\ . \label{surfvir}\]

El aporte restante se debe a las fuerzas interpartículas. Por lo tanto,

\[{p\over \kT}={N\over V}-{1\over 3V\kT}\>\blangle\sum_i \Bx\ns_i\cdot\bnabla\ns_{\!i}W\brangle\ .\]

Invocando la definición de\(g(r)\), tenemos

\[p=n\kT\,\left\{1-{2\pi n\over 3\kT}\!\int\limits_0^\infty\!\!dr\>r^3\,g(r)\,u'(r)\right\}\ .\]

Como derivación alternativa, considerar la Primera Ley de la Termodinámica,

\[d\Omega=-S\,dT - p\,dV -N\,d\mu\ ,\]

de la que derivamos

\[p=-\pabc{\Omega}{V}{T,\mu}=-\pabc{F}{V}{T,N}\ .\]

Ahora vamos\(V\to\ell^3 V\), donde\(\ell\) es un parámetro de escala. Entonces

\[p=-{\pz\Omega\over\pz V}=-{1\over 3V}\,{\pz\over\pz\ell}\Bigg|\nd_{\ell=1}\!\Omega(T,\ell^3 V,\mu)\ .\]

Ahora

\[\begin{split} \Xi(T,\ell^3V,\mu)&=\sum_{N=0}^\infty {1\over N!}\,e^{\beta\mu N}\,\lambda_T^{-3N}\!\!\int\limits_{\ell^3 V}\!\!\!d^3\!x\ns_1\cdots\!\! \int\limits_{\ell^3 V}\!\!\!d^3\!x\ns_N\>e^{-\beta W(\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N)}\\ &=\sum_{N=0}^\infty {1\over N!}\,\Big( e^{\beta\mu}\,\lambda_T^{-3}\Big)^N\ell^{3N}\!\!\int\limits_V\!\!d^3\!x\ns_1\cdots\!\! \int\limits_V\!\!d^3\!x\ns_N\>e^{-\beta W(\ell\Bx\ns_1\,,\,\ldots\,,\,\ell\Bx\ns_N)} \end{split}\]

Por lo tanto,

\[\begin{split} p&=-{1\over 3V}\,{\pz\Omega(\ell^3 V)\over\pz\ell}\Bigg|_{\ell=1} = {\kT\over 3V}\,{1\over\Xi}\,{\pz\Xi(\ell^3 V)\over\pz\ell}\\ &={\kT\over 3V}\,{1\over\Xi}\,\sum_{N=0}^\infty {1\over N!}\big(z\lambda_T^{-3}\big)^N\left\{ \int\limits_V\!\!d^3\!x\ns_1\cdots\int\limits_V\!\!d^3\!x\ns_N\,e^{-\beta W(\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N)}\Bigg[3N-\beta\sum_i \Bx\ns_i\cdot {\pz W\over\pz\Bx\ns_i}\Bigg]\right\}\\ &=n\kT-{1\over 3V}\,\Big\langle{\pz W\over\pz\ell}\Big\rangle\nd_{\ell=1}\ . \end{split}\]

Por último, desde\(W=\sum_{i<j}u(\ell\Bx\ns_{ij})\) tenemos

\[\begin{split} \Big\langle{\pz W\over\pz\ell}\Big\rangle\nd_{\ell=1}&=\sum_{i<j}\Bx\ns_{ij}\cdot\bnabla u(\Bx\ns_{ij})\\ &={2\pi N^2\over V}\!\int\limits_0^\infty\!\!dr\,r^3 g(r)\,u'(r)\ , \end{split}\]

y por lo tanto

\[p=n\kT -\frac{2}{3}\pi n^2\!\int\limits_0^\infty\!\!dr\,r^3\,g(r)\,u'(r)\ .\]

Obsérvese que la densidad\(n\) ingresa a la ecuación de estado explícitamente en el RHS de la ecuación anterior, pero también implícitamente a través de la función de distribución de pares\(g(r)\), que tiene dependencia implícita de ambos\(n\) y\(T\).

Correlaciones y dispersión

Considera la dispersión de un haz de luz o partículas (fotones o neutrones) de un líquido. Etiquetamos los estados de las partículas del haz por su evector de ondas\(\Bk\) y asumimos una dispersión general\(\ve\ns_\Bk\). Para fotones,\(\ve\ns_\Bk=\hbar c |\Bk|\), mientras que para neutrones\(\ve\ns_\Bk=\hbar^2\Bk^2/2 m\ns_\Rn\). Asumimos un solo proceso de dispersión con el líquido, durante el cual se conserva el impulso total y la energía del líquido más haz. Escribimos

\[\begin{split} \Bk'&=\Bk+\Bq\\ \ve\ns_{\Bk'}&=\ve\ns_\Bk+\hbar\omega\ , \end{split}\]

donde\(\Bk'\) está el estado final de la partícula de haz dispersado. Así, el fluido transfiere impulso\(\RDelta\Bp= \hbar\Bq\) y energía\(\hbar\omega\) al haz.

Figura\(\PageIndex{3}\): En un experimento de dispersión, un haz de partículas interactúa con una muestra y las partículas del haz dispersan las partículas de la muestra. Un impulso\(\hbar\Bq\) y energía\(\hbar\omega\) se transfieren a la partícula del haz durante dicha colisión. Si\(\omega=0\), se dice que la dispersión es elástica. Porque\(\omega\ne 0\), la dispersión es inelástica.

Consideremos ahora el proceso de dispersión entre un estado inicial\(\sket{i,\Bk}\) y un estado final\(\sket{j,\Bk'}\), donde estos estados describen tanto el haz como el líquido. Según la regla de oro de Fermi, la tasa de dispersión es

\[\Gamma\ns_{i\Bk\to j\Bk'}={2\pi\over\hbar}\,\big|\sexpect{j,\Bk'}{\CV}{i,\Bk}\big|^2\, \delta(E\ns_j-E\ns_i+\hbar\omega)\ ,\]

donde\(\CV\) está el potencial de dispersión y\(E\ns_i\) es la energía interna inicial del líquido. Si\(\Br\) es la posición de la partícula del haz y\(\{\Bx\ns_l\}\) son las posiciones de las partículas líquidas, entonces

\[\CV(\Br)=\sum_{l=1}^N v(\Br-\Bx\ns_l)\ .\]

La sección transversal de dispersión diferencial (por unidad de frecuencia por unidad de ángulo sólido) es

\[{\pz^2\!\sigma\over\pz\Omega\,\pz\omega}={\hbar\over 4\pi}\,{g(\ve\ns_{\Bk'})\over |\Bv\ns_\Bk|}\sum_{i,j} P\ns_i\, \Gamma\ns_{i\Bk\to j\Bk'}\ ,\]

donde

\[g(\ve)=\int\!\!{d^d\!k\over (2\pi)^d}\,\delta(\ve-\ve\ns_\Bk)\]

es la densidad de estados para la partícula del haz y

\[P\ns_i={1\over Z}\,e^{-\beta E\ns_i}\ .\]

Consideremos ahora el elemento matriz

\[\begin{split} \expect{j,\Bk'}{\CV}{i,\Bk}&=\expect{j} {{1\over V}\sum_{l=1}^N\int\!\!d^d\!r e^{i(\Bk-\Bk')\cdot\Br}\,v(\Br-\Bx\ns_l)}{i}\\ &={1\over V}\> {\hat v}(\Bq)\>\expect{j}{\sum_{l=1}^N e^{-i\Bq\cdot\Bx\ns_l}}{i}\ , \end{split}\]

donde hemos asumido que los haces incidentes y dispersos son ondas planas. Entonces tenemos

\[\begin{split} {\pz^2\!\sigma\over\pz\Omega\,\pz\omega}&={\hbar\over 2}\,{g(\ve\ns_{\Bk+\Bq})\over |\bnabla\nd_{\!\!\Bk} \ve\ns_\Bk|}\,{|{\hat v}(\Bq)|^2\over V^2}\sum_i P\ns_i\ \sum_j \big|\expect{j}{\sum_{l=1}^N e^{-i\Bq\cdot\Bx\ns_l}}{i}\big|^2\,\delta(E\ns_j-E\ns_i+\hbar\omega)\\ &={g(\ve\ns_{\Bk+\Bq})\over 4\pi\, |\bnabla\nd_{\!\!\Bk} \ve\ns_\Bk|}\,{N\over V^2}\,|{\hat v}(\Bq)|^2\>S(\Bq,\omega)\ , \end{split}\]

donde\(S(\Bq,\omega)\) está el factor de estructura dinámica,

\[S(\Bq,\omega)={2\pi\hbar\over N}\sum_i P\ns_i\ \sum_j \big|\expect{j}{\sum_{l=1}^N e^{-i\Bq\cdot\Bx\ns_l}}{i}\big|^2\,\delta(E\ns_j-E\ns_i+\hbar\omega)\]

Tenga en cuenta que para un operador arbitrario\(A\),

\[\begin{split} \sum_j \big|\expect{j}{A}{i}\big|^2\,\delta(E\ns_j-E\ns_i+\hbar\omega)&={1\over 2\pi\hbar}\,\sum_j \! \int\limits_{-\infty}^\infty\!\!\!dt\>e^{i(E\ns_j-E\ns_i+\hbar\omega)\,t/\hbar}\>\expect{i}{A\yd}{j}\,\expect{j}{A}{i}\\ &={1\over 2\pi\hbar}\,\sum_j \!\int\limits_{-\infty}^\infty\!\!\!dt\>e^{i\omega t}\,\expect{i} {A\yd}{j}\,\expect{j}{e^{i\HH t/\hbar}\,A\,e^{-i\HH t/\hbar}}{i}\\ &={1\over 2\pi\hbar}\!\int\limits_{-\infty}^\infty\!\!\!dt\>e^{i\omega t}\,\expect{i}{A\yd(0)\,A(t)}{i}\ . \end{split}\]

Por lo tanto,

\[\begin{split} S(\Bq,\omega)&={1\over N}\!\!\int\limits_{-\infty}^\infty\!\!\!dt\>e^{i\omega t}\>\sum_i P\ns_i\, \expect{i}{\sum_{l,l'} e^{i\Bq\cdot\Bx\ns_l(0)}\,e^{-i\Bq\cdot\Bx\ns_{l'}(t)}}{i}\\ &={1\over N}\!\!\int\limits_{-\infty}^\infty\!\!\!dt\>e^{i\omega t}\>\blangle \sum_{l,l'} e^{i\Bq\cdot\Bx\ns_l(0)}\,e^{-i\Bq\cdot\Bx\ns_{l'}(t)}\brangle\ , \end{split}\]

donde los corchetes angulares en la última línea denotan un valor de expectativa térmica de un operador mecánico cuántico. Si integramos en todas las frecuencias, obtenemos el correlador de tiempo igual,

\[\begin{split} S(\Bq)&=\!\!\int\limits_{-\infty}^\infty\!\!{d\omega\over 2\pi}\>S(\Bq,\omega) ={1\over N}\sum_{l,l'} \blangle e^{i\Bq\cdot(\Bx\ns_l-\Bx\ns_{l'})}\brangle\\ &=N\,\delta\ns_{\Bq,0}+1+n\!\!\int\!\!d^d\!r\,e^{-i\Bq\cdot\Br}\,\big[g(r)-1\big]\ . \label{staticstructure} \end{split}\]

conocido como el factor de estructura estática ¹⁰. Tenga en cuenta que\(S(\Bq=0)=N\), ya que todas las fases\(e^{i\Bq\cdot(\Bx\ns_i-\Bx\ns_j)}\) son entonces unidad. Como\(q\to\infty\), las fases oscilan rápidamente con los cambios en las distancias\(|\Bx\ns_i-\Bx\ns_j|\), y promedian a cero. No obstante, los términos 'diagonales' en la suma, los que tienen\(i=j\), siempre aportan un total de\(1\) a\(S(\Bq)\). Por lo tanto en el\(q\to\infty\) límite que tenemos\(S(q\to\infty)=1\).

En general, los detectores utilizados en un experimento de dispersión son sensibles a la energía de las partículas dispersas del haz, aunque siempre hay una resolución experimental finita, tanto en\(\Bq\) como\(\omega\). Esto significa que lo que se mide es en realidad algo así como

\[S\ns_{meas}(\Bq,\omega)=\int\!\!d^d\!q'\int\!d\omega'\,F(\Bq-\Bq')\,G(\omega-\omega')\,S(\Bq',\omega')\ ,\]

donde\(F\) y\(G\) son esencialmente funciones gaussianas de su argumento, con ancho dado por la resolución experimental. Si uno se integra sobre todas las frecuencias\(\omega\), si uno simplemente cuenta partículas dispersas en función de\(\Bq\) pero sin discriminación alguna de sus energías, entonces se mide el factor de estructura estática\(S(\Bq)\). La dispersión elástica está determinada por\(S(\Bq,\omega=0\), sin transferencia de energía.

Figura\(\PageIndex{4}\): Comparación del factor de estructura estática determinado por el trabajo de dispersión de neutrones de J. L. Yarnell, Phys. Rev. A 7, 2130 (1973) con cálculos de dinámica molecular de Verlet (1967) para un fluido Lennard-Jones.

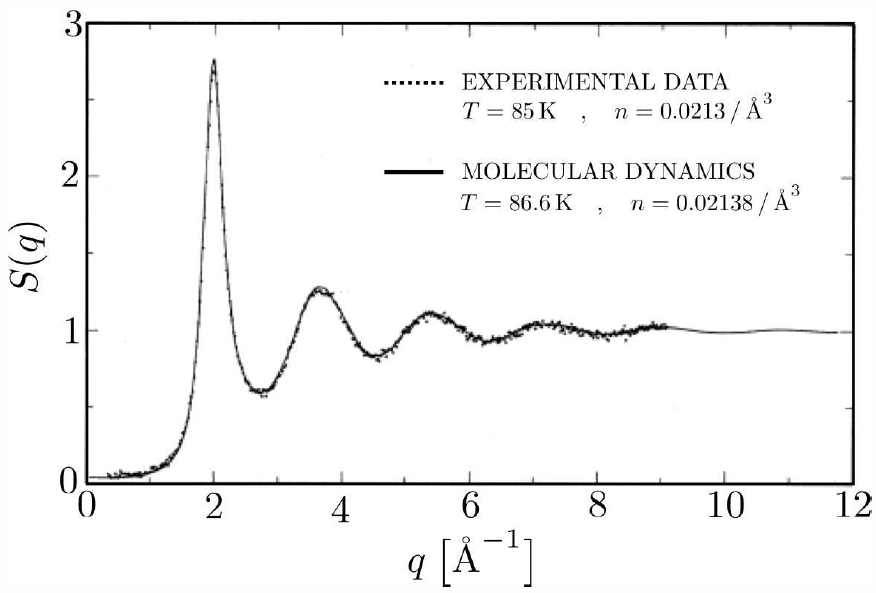
Correlación y respuesta

Supongamos que también\(v(\Bx)\) está presente un potencial externo. Entonces

\[P(\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N)={1\over Q\ns_N[v]}\cdot {1\over N!}\,e^{-\beta W(\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N)}\, e^{-\beta\sum_i v(\Bx\ns_i)}\ ,\]

donde

\[Q\ns_N[ v]={1\over N!}\!\int\!\!d^d\!x\ns_1\cdots\!\int\!\!d^d\!x\ns_N\,e^{-\beta W(\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N)}\,e^{-\beta\sum_i v(\Bx\ns_i)}\ .\]

La energía libre de Helmholtz es entonces

\[F=-{1\over\beta}\,\ln\Big(\lambda_T^{-dN}\,Q\ns_N[ v]\Big)\ .\]

Ahora considere la derivada funcional

\[{\delta F\over\delta v(\Br)}=-{1\over\beta}\cdot{1\over Q\ns_N}\cdot{\delta Q\nd_N\over\delta v(\Br)}\ .\]

Usando

\[\sum_i v(\Bx\ns_i)=\int\!\!d^d\!r\, v(\Br)\,\sum_i\delta(\Br-\Bx\ns_i)\ ,\]

de ahí

\[\begin{aligned} {\delta F\over\delta v(\Br)}&=\int\!\!d^d\!x\ns_1\cdots\!\int\!\!d^d\!x\ns_N\,P(\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N)\, \sum_i\delta(\Br-\Bx\ns_i)\nonumber\\ &=n\ns_1(\Br)\ ,\end{aligned}\]

que es la densidad local en\(\Br\).

A continuación, considere la función de respuesta,

\[\begin{split} \xhi(\Br,\Br')&\equiv {\delta n\ns_1(\Br) \over\delta v(\Br') }={ \delta^2\! F[ v] \over \delta v(\Br)\,\delta v(\Br') }\\ &={1\over\beta}\cdot{1\over Q_N^2}\,{\delta Q\ns_N\over\delta v(\Br)}\,{\delta Q\ns_N\over\delta v(\Br')} -{1\over\beta}\cdot {1\over Q\ns_N} \, {\delta^2\!Q\ns_N\over\delta v(\Br)\,\delta v(\Br')}\bvph\\ &=\beta\,n\ns_1(\Br)\,n\ns_1(\Br') - \beta\,n\ns_1(\Br)\,\delta(\Br-\Br') - \beta\,n\ns_2(\Br,\Br')\ . \end{split}\]

En un sistema isotrópico,\(\xhi(\Br,\Br')=\xhi(\Br-\Br')\) es una función de la separación de coordenadas, y

\[\begin{split} -\kT\,\chi(\Br-\Br')&=-n^2 + n\,\delta(\Br-\Br') + n^2 g\big(|\Br-\Br'|\big)\bvph\\ &=n^2\,h\big(|\Br-\Br'|\big) + n\,\delta(\Br-\Br')\ . \end{split}\]

Tomando la transformada de Fourier,

\[-\kT\,{\hat\chi}(\Bq)=n+n^2\,{\hat h}(\Bq)=n \,S(\Bq)\ .\]

También podemos escribir

\[{\kappa\ns_T\over\kappa^0_T}=1+n\,{\hat h}(0)=-n\kT\,{\hat\chi}(0)\ ,\]

\(\kappa\ns_T=-\Hxhi(0)\).

¿Qué significa todo esto? Supongamos que tenemos un sistema isotrópico que está sujeto a un potencial débil, espacialmente inhomogéneo\(v(\Br)\). Esperamos que la densidad\(n(\Br)\) en presencia del potencial no homogéneo a sí mismo sea no homogénea. Las primeras correcciones al\(v=0\) valor\(n=n_0\) son lineales en\(v\), y dadas por

\[\begin{split} \delta n(\Br)&=\int\!\!d^d\!r'\>\xhi(\Br,\Br')\, v(\Br')\\ &=-\beta n_0\, v(\Br) - \beta n_0^2\!\int\!\!d^d\!r'\>h(\Br-\Br)\, v(\Br')\ . \end{split}\]

Tenga en cuenta\(v(\Br)>0\) que si se vuelve energéticamente más costoso para una partícula estar en\(\Br\). En consecuencia, la respuesta de densidad es negativa, y proporcional a la relación\(v(\Br)/\kT\) —este es el primer término en la ecuación anterior. Si no hubiera correlaciones entre las partículas, entonces\(h=0\) y esta sería toda la historia. Sin embargo, las partículas en general están correlacionadas. Consideremos, por ejemplo, el caso de las esferas duras de diámetro\(a\), y que haya un potencial repulsivo en\(\Br=0\). Esto significa que es menos probable que una partícula esté centrada en cualquier lugar dentro de una distancia\(a\) del origen. Pero entonces será más probable encontrar una partícula en la próxima 'concha' de espesor radial\(a\).

Jerarquía BBGKY

Las funciones de distribución satisfacen una jerarquía de ecuaciones integrodiferenciales conocida como la jerarquía BBGKY ¹¹. En sistemas homogéneos, tenemos

\[g\ns_k(\rok)={N!\over (N-k)!}\,{1\over n^k}\!\int\!\!d^d\!x\ns_{k+1}\cdots\!\int\!\!d^d\!x\ns_N\,P(\rok\,,\,\Bx\ns_{k+1}\,,\,\ldots\,,\,\Bx\ns_N)\ ,\]

donde

\[P(\xoN)={1\over Q\ns_N}\cdot{1\over N!}\>e^{-\beta W(\xoN)}\ .\]

Tomando el gradiente con respecto a\(\Br\ns_1\), tenemos

\[\begin{split} {\pz\over\pz\Br\ns_1}g\ns_k(\rok)&={1\over Q\ns_N}\cdot{n^{-k}\over (N-k)!}\!\int\!\!d^d\!x\ns_{k+1}\cdots\!\int\!\!d^d\!x\ns_N\, e^{-\beta\sum_{k<i<j}u(\Bx\ns_{ij})}\\ &\qquad\qquad\times{\pz\over\pz\Br\ns_1}\bigg[ e^{-\beta\sum_{i<j\le k} u(\Br\ns_{ij})}\cdot e^{-\beta\sum_{i\le k < j}u(\Br\ns_i-\Bx\ns_j)}\bigg]\ , \end{split}\]

donde\(\sum_{k<i<j}\) significa sumar en índices\(i\) y de\(j\) tal manera que\(i<j\) y\(k<i\),

\[\begin{aligned} \sum_{k<i<j}u(\Bx\ns_{ij})&\equiv \sum_{i=k+1}^{N-1} \sum_{j=i+1}^Nu\big(\Bx\ns_i-\Bx\ns_j\big)\\ \sum_{i<j\le k}u(\Br\ns_{ij})&\equiv \sum_{i=1}^{k-1} \sum_{j=i+1}^k u\big(\Br\ns_i-\Br\ns_j\big)\\ \sum_{i\le k < j}u(\Br\ns_i-\Bx\ns_j)&=\sum_{i=1}^k \sum_{j=k+1}^N u(\Br\ns_i-\Bx\ns_j)\ .\end{aligned}\]

Ahora

\[\begin{split} {\pz\over\pz\Br\ns_1}\bigg[ e^{-\beta\sum_{i<j\le k} u(r\ns_{ij})}\cdot e^{-\beta\sum_{i\le k < j}u(\Br\ns_i-\Bx\ns_j)}\bigg]=\\ &\hskip-2.4in\beta\>\Bigg\{\!\sum_{1<j\le k} {\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\ + \sum_{k<j} {\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\Bigg\} \cdot\bigg[ e^{-\beta\sum_{i<j\le k} u(r\ns_{ij})}\cdot e^{-\beta\sum_{i\le k < j}u(\Br\ns_i-\Bx\ns_j)}\bigg]\ \ , \end{split}\]

de ahí

\[\begin{split} {\pz\over\pz\Br\ns_1}g\ns_k(\rok)&=-\beta\sum_{j=2}^k{\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\,g\ns_k(\rok)\\ &\qquad-\beta(N-k)\!\int\!\!d^d\!x\ns_{k+1}\,{\pz u(\Br\ns_1-\Bx\ns_{k+1})\over\pz\Br\ns_1}\,P(\rok\,,\,\Bx\ns_{k+1}\,,\,\ldots\,,\,\Bx\ns_N)\\ &=-\beta\sum_{j=2}^k{\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\,g\ns_k(\rok)\\ &\hskip1.1in +n\!\int\!\!d^d\!x\ns_{k+1}\,{\pz u(\Br\ns_1-\Bx\ns_{k+1})\over\pz\Br\ns_1}\,g\ns_{k+1}(\rok\,,\,x\ns_{k+1})\quad. \end{split}\]

Así, obtenemos la jerarquía BBGKY:

\[\begin{split} -\kT\,{\pz\over\pz\Br\ns_1}g\ns_k(\rok)&=\sum_{j=2}^k{\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\,g\ns_k(\rok)\\ &\qquad\qquad + n\!\int\!\!d^d\!r'\,{\pz u(\Br\ns_1-\Br')\over\pz\Br\ns_1}\,g\ns_{k+1}(\rok\,,\,\Br')\quad. \end{split}\]

La jerarquía BBGKY es una torre infinita de ecuaciones integro-diferenciales acopladas, relacionadas con\(g\ns_k\)\(g\ns_{k+1}\) para todos\(k\). Si aproximamos\(g\ns_k\) a algún nivel\(k\) en términos de distribuciones de orden igual o inferior, entonces obtenemos un conjunto cerrado de ecuaciones que en principio pueden resolverse, al menos numéricamente. Por ejemplo, la aproximación de Kirkwood cierra la jerarquía en orden\(k=2\) imponiendo la condición

\[g\ns_3(\Br\ns_1\,,\,\Br\ns_2\,,\,\Br\ns_3)\equiv g(\Br\ns_1-\Br\ns_2)\,g(\Br\ns_1-\Br\ns_3)\,g(\Br\ns_2-\Br\ns_2)\ .\]

Esto da como resultado la única ecuación integrodiferencial

\[-\kT\,\bnabla g(\Br)=g(\Br)\,\bnabla u + n\!\int\!\!d^d\!r'\,g(\Br)\,g(\Br')\,g(\Br-\Br')\,\bnabla u(\Br-\Br')\ .\]

Esto se conoce como la ecuación Nacido-Verde-Yvon (BGY). En la práctica, la ecuación BGY, que se resuelve numéricamente, da resultados adecuados sólo a bajas densidades.

Teoría de Ornstein-Zernike

La función de correlación directa\(c(\Br)\) se define por la ecuación

\[h(\Br)=c(\Br) + n\!\int\!\!d^3\!r'\>h(\Br-\Br')\,c(\Br')\ ,\]

donde\(h(r)=g(r)-1\) y asumimos un sistema isotrópico. A esto se le llama la ecuación de Ornstein-Zernike. El primer término,\(c(\Br)\), da cuenta de correlaciones locales, que luego se propagan en el segundo término para dar cuenta de correlaciones de largo alcance.

La ecuación OZ es una ecuación integral, pero se convierte en una simple algebraica tras la transformación de Fourier:

\[{\hat h}(\Bq)={\hat c}(\Bq) + n\,{\hat h}(\Bq)\,{\hat c}(\Bq)\ ,\]

cuya solución es

\[{\hat h}(\Bq)={{\hat c}(\Bq)\over 1-n\,{\hat c}(\Bq)}\ .\]

El factor de estructura estática es entonces

\[S(\Bq)=1+n\,{\hat h}(\Bq)={1\over 1-n\,{\hat c}(\Bq)}\ .\]

En el gran conjunto canónico, podemos escribir

\[\kappa\ns_T={1+n\,{\hat h}(0)\over n\kT}={1\over n\kT}\cdot{1\over 1-n\,{\hat c}(0)} \qquad\Longrightarrow\qquad n\,{\hat c}(0)=1-{\kappa^0_T\over\kappa\ns_T}\ ,\]

donde\(\kappa^0_T=1/n\kT\) está la compresibilidad isotérmica de gas ideal.

En este punto, simplemente hemos sustituido una función desconocida,\(h(\Br)\), por otra, a saber\(c(\Br)\). Para cerrar el sistema, necesitamos\(c(\Br)\) relacionarnos de\(h(\Br)\) nuevo de alguna manera. Existen diversos esquemas de aproximación que hacen precisamente esto.

Ecuación Percus-Yevick

En la aproximación Percus-Yevick, tomamos

\[c(\Br)=\big[1-e^{\beta u(\Br)}\big]\cdot g(\Br)\ .\]

Tenga en cuenta que se\(c(\Br)\) desvanece cada vez que el\(u(\Br)\) propio potencial se desvanece. Esto da como resultado la siguiente ecuación integro-diferencial para la función de distribución de pares\(g(\Br)\):

\[g(\Br)=e^{-\beta u(\Br)}+n\,e^{-\beta u(\Br)}\!\int\!\!d^3\!r'\>\big[g(\Br-\Br')-1\big]\cdot\big[1-e^{\beta u(\Br')}\big]\,g(\Br')\ .\]

Esta es la ecuación Percus-Yevick. Notablemente, la ecuación Percus-Yevick (PY) se puede resolver analíticamente para el caso de esferas duras, dónde\(u(r)=\infty\) para\(r\le a\) y\(u(r)=0\) para\(r>a\), dónde\(a\) está el diámetro de la esfera dura. Definir la función\(y(\Br)=e^{\beta u(\Br)}g(\Br)\), en cuyo caso

\[c(\Br)=y(\Br)\,f(\Br)=\begin{cases} -y(\Br) & ,\ r\le a \\ 0 & ,\ r>a\ . \end{cases}\]

Aquí,\(f(\Br)=e^{-\beta u(\Br)}-1\) está la función Mayer. Observamos que la definición de\(y(\Br)\) puede causar cierta preocupación por el sistema de esfera dura, por el\(e^{\beta u(\Br)}\) término, que diverge severamente para\(r\le a\). Sin embargo, se\(g(r)\) desvanece en este límite, ¡y su producto\(y(\Br)\) es de hecho finito! La ecuación PY puede entonces escribirse para la función\(y(\Br)\) como

\[y(\Br)=1+n\!\!\!\int\limits_{r'<a}\!\!\!\!d^3\!r'\>y(\Br')-n\!\!\!\!\!\!\!\int\limits_{r'<a\atop |\Br-\Br'|>a}\!\!\!\!\!\!\!\!d^3\!r'\>y(\Br')\,y(\Br-\Br')\ .\]

Esto ha sido resuelto utilizando los métodos de transformación de Laplace por M. S. Wertheim, J. Math. Phys. 5, 643 (1964). El resultado final para\(c(\Br)\) es

\[c(\Br)=-\left\{\lambda\ns_1 + 6\eta\,\lambda_2\,\Big({r\over a}\Big) + \half \eta\,\lambda_1\,\Big({r\over a}\Big)^3\right\}\cdot\RTheta(a-r)\ , \label{PYdcf}\]

donde\(\eta=\frac{1}{6}\pi a^3 n\) esta la fraccion de empaque y

\[\lambda\ns_1={(1+2\eta)^2\over (1-\eta)^4} \qquad,\qquad\lambda_2=-{(1+\half\eta)^2\over (1-\eta)^4}\ . \label{PYlambdas}\]

Esto lleva a la ecuación de estado

\[p=n\kT\cdot{1+\eta+\eta^2\over (1-\eta)^3}\ . \label{PYesa}\]

Esto se pone\(B\ns_2\) y\(B\ns_3\) es exactamente correcto. La precisión de la aproximación PY para los coeficientes viriales de orden superior se muestra en la tabla [pytab].

Para obtener la ecuación de estado a partir de la ecuación ref {PyDCF}, invocamos la ecuación de compresibilidad,

\[n\kT\,\kappa\ns_T=\pabc{n}{p}{T}={1\over 1-n\,{\hat c}(0)}\ .\]

Por lo tanto, necesitamos

\[\begin{split} {\hat c}(0)&=\int\!\!d^3\!r\,c(\Br)\\ &=-4\pi a^3\!\!\int\limits_0^1\!\!dx\,x^2\,\left[\lambda\ns_1 + 6\,\eta\,\lambda\ns_2\,x + \half\,\eta\,\lambda\ns_1\,x^3\right]\\ &=-4\pi a^3\left[\frac{1}{3}\,\lambda\ns_1 + \frac{3}{2}\,\eta\,\lambda\ns_2 + \frac{1}{12}\,\eta\,\lambda\ns_1\right]\ . \end{split}\]

Con\(\eta=\frac{1}{6}\pi a^3 n\) y usando las definiciones de\(\lambda\ns_{1,2}\) en la ecuación\ ref {pilambdas}, se encuentra

\[1-n\,{\hat c}(0)={1+4\eta+4\eta^2\over (1-\eta)^4}\ .\]

Entonces tenemos, a partir de la ecuación de compresibilidad,

\[{6\kT\over \pi a^3}\,{\pz p\over\pz\eta}={1+4\eta+4\eta^2\over (1-\eta)^4}\ .\]

Integrando, obtenemos\(p(\eta)\) hasta una constante. La constante se establece para que\(p=0\) cuando\(n=0\). El resultado es Ecuación\ ref {PyESA}.

Cuadro [pytab]: Comparación de los resultados exactos (Monte Carlo) con los de la aproximación de cadenas Percus-Yevick (PY) e hipernetted chains (HCA) para esferas duras en tres dimensiones. Fuentes: Hansen y McDonald (1990) y Reichl (1998)

cantidad	exacta	PY	HNC
\(B_4/B_2^3\)	0.28695	0.2969	0.2092
\(B_5/B_2^4\)	0.1103	0.1211	0.0493
\(B_6/B_2^5\)	0.0386	0.0281	0.0449
\(B_7/B_2^6\)	0.0138	0.0156	—

Otro esquema de uso común es la aproximación de cadenas hiperconectadas (HNC), para la cual

\[c(\Br)=-\beta u(\Br) + h(\Br) - \ln\!\Big(1+h(\Br)\Big)\ .\]

La justificación del HNC y otros esquemas de aproximación se basa en enfoques diagramáticos, que son extensiones de la expansión del clúster de Mayer para el cálculo de funciones de correlación. Para detalles y referencias a su aplicación en la literatura, véase Hansen y McDonald (1990) y Reichl (1998).

Aproximación Ornstein-Zernike a longitudes de onda largas

Ampliemos la función de correlación directa\({\hat c}(\Bq)\) en potencias del oleaje\(\Bq\), a saber.

\[\Hc(\Bq)=\Hc(0)+c\ns_2\,q^2 + c\ns_4\,q^4 + \ldots\ .\]

Aquí hemos asumido la isotropía espacial. Entonces

\[\begin{split} 1-n\,\Hc(\Bq)&={1\over S(\Bq)}=1-n\,\Hc(0)-n\,c\ns_2\,q^2 + \ldots\\ &\equiv \xi^{-2} R^2+ q^2 R^2 + \CO(q^4)\ , \end{split}\]

donde

\[R^2=-n\,c\ns_2 = 2\pi n\!\!\int\limits_0^\infty \!\!dr\,r^4\,c(r)\]

y

\[\xi^{-2}={1-n\,\Hc(0)\over R^2}={1-4\pi n\!\int_0^\infty\!\!dr\,r^2\,c(r)\over 2\pi n\!\int_0^\infty \!\!dr\,r^4\,c(r)}\ .\]

La cantidad nos\(R(T)\) dice algo sobre el rango efectivo de las interacciones, mientras que\(\xi(T)\) es la longitud de correlación. A medida que nos acercamos a un punto crítico, la longitud de correlación diverge como una ley de poder:

\[\xi(T)\sim A |T-T\ns_\Rc|^{-\nu}\ .\]

La susceptibilidad viene dada por

\[\Hxhi(\Bq)=-n\beta\, S(\Bq)=-{n\beta R^{-2}\over \xi^{-2}+ q^2 + \CO(q^4)}\]

En la aproximación Ornstein-Zernike, uno deja caer los\(\CO(q^4)\) términos en el denominador y conserva solo el comportamiento de longitud de onda larga. en la función de correlación directa. Por lo tanto,

\[\xhihOZ(\Bq)=-{n\beta R^{-2}\over\xi^{-2}+q^2}\ .\]

Ahora aplicamos la transformada inversa de Fourier de nuevo al espacio real para obtener\(\xhiOZ(\Br)\). En\(d=1\) dimensión el resultado se puede obtener exactamente:

\[\begin{split} \xhiOZ_{d=1}(x)&=-{n\over\kT R^2}\!\int\limits_{-\infty}^\infty\!\!{dq\over 2\pi}\>{e^{iqx}\over \xi^{-2}+q^2}\\ &=-{n\xi\over 2\kT R^2}\,e^{-|x|/\xi}\ . \end{split}\]

En dimensiones superiores\(d>1\) podemos obtener el resultado asintóticamente en dos límites:

• Tomar\(r\to \infty\) con\(\xi\) fijo. Entonces\[\xhiOZ_d(\Br)\simeq -C\ns_d \,n\cdot{\xi^{(3-d)/2}\over \kT\,R^2}\cdot{e^{-r/\xi}\over r^{(d-1)/2}}\cdot\left\{1+\CO\bigg({d-3\over r/\xi}\bigg)\right\}\ ,\] donde\(C\ns_d\) están las constantes adimensionales.
• Tomar\(\xi\to\infty\) con\(r\) fijo; este es el límite\(T\to T\ns_\Rc\) en fijo\(r\). En dimensiones\(d>2\) obtenemos\[\xhiOZ_d(\Br)\simeq -{C'_d\, n\over\kT R^2}\cdot{e^{-r/\xi}\over r^{d-2}}\cdot \left\{1+\CO\bigg({d-3\over r/\xi}\bigg)\right\}\ .\] En\(d=2\) dimensiones obtenemos\[\xhiOZ_{d=2}(\Br)\simeq-{C'_2\,n\over\kT R^2}\cdot\ln\!\bigg({r\over\xi}\bigg)\,e^{-r/\xi}\cdot\left\{1+\CO\bigg({1\over\ln(r/\xi)}\bigg)\right\}\ ,\] donde las\(C'_d\) son constantes adimensionales.

En la criticidad\(\xi\to\infty\),, y claramente nuestros resultados\(d=1\) y\(d=2\) dimensiones no tienen sentido, ya que son divergentes. Para corregir este comportamiento, M. E. Fisher en 1963 sugirió que las funciones de correlación OZ en el\(r\ll \xi\) límite sean reemplazadas por

\[\xhi(\Br)\simeq -C''_d\,n \cdot {\xi^\eta\over \kT R^2}\cdot{e^{-r/\xi}\over r^{d-2+\eta}}\ ,\]

un resultado conocido como escalamiento anómalo. Aquí,\(\eta\) está el exponente anómalo de escalado.

Recordemos que la compresibilidad isotérmica viene dada por\(\kappa\ns_T=-\Hxhi(0)\). Cerca de la criticidad, la integral en\(\Hxhi(0)\) está dominada por la\(r\ll\xi\) parte, ya que\(\xi\to\infty\). Así, usando el escalado anómalo de Fisher,

\[\begin{split} \kappa\ns_T=-\Hxhi(0)&=-\int\!\!d^d\!r\,\xhi(\Br)\\ &\sim A\!\int\!\!d^d\!r\>{e^{-r/\xi}\over r^{d-2+\eta}} \sim B\,\xi^{2-\eta}\sim C\,\big|T-T\ns_\Rc\big|^{-(2-\eta)\nu}\ , \end{split}\]

donde\(A\),\(B\), y\(C\) son constantes dependientes de la temperatura que no son singulares en\(T=T\ns_\Rc\). Así, ya que\(\kappa\ns_T\propto |T-T\ns_\Rc|^{-\gamma}\), concluimos

\[\gamma=(2-\eta)\,\nu\ ,\]

un resultado conocido como hiperescalamiento.