6.5: Sistemas de Coulomb - Plasmas y el Gas Electrónico

Template:MathJaxArovas

Potencial electrostático

Los sistemas de culomb son particularmente interesantes en la mecánica estadística debido a sus fuerzas de largo alcance, que resultan en el fenómeno de tamizaje. Las fuerzas de largo alcance causan estragos con la expansión del clúster de Mayer, ya que la función Mayer ya no es integrable. Así, la expansión virial falla, y es necesario aplicar nuevas técnicas para revelar la física de los plasmas.

La energía potencial de un sistema Coulomb es

\[U=\half\!\int\!\!d^d\!r\!\int\!\!d^d\!r'\,\rho(\Br)\,u(\Br-\Br')\,\rho(\Br')\ ,\]donde\(\rho(\Br)\) está la densidad de carga y\(u(\Br)\), que tiene las dimensiones de (energía)\(/\) (carga)\({}^2\), satisface

\[\nabla^2 u(\Br-\Br')=-4\pi\,\delta(\Br-\Br')\ .\]Por lo tanto,

\[u(\Br)=\begin{cases} -2\pi\,|x-x'| & ,\ d=1 \\ &\\ -2\,\ln|\Br-\Br'| & , \ d=2 \\ &\\ |\Br-\Br'|^{-1} & , \ d=3\ . \end{cases}\]

Para partículas de disco, la densidad de carga\(\rho(\Br)\) viene dada por

\[\rho(\Br)=\sum_i q\ns_i\,\delta(\Br-\Bx\ns_i)\ ,\]donde\(q\ns_i\) está la carga de la\(i^{th}\) partícula. Asumiremos dos tipos de cargos:\(q=\pm e\), con\(e>0\). El potencial eléctrico es

\[\phi(\Br)=\int\!\!d^d\!r'\,u(\Br-\Br')\,\rho(\Br')=\sum_i q\nd_i\,u\ns(\Br-\Bx\ns_i)\ .\]Esto satisface la ecuación de Poisson,

\[\nabla^2\phi(\Br)=-4\pi\rho(\Br)\ .\]La energía potencial total se puede escribir como

\[U=\half\!\int\!\!d^d\!r\,\phi(\Br)\,\rho(\Br)=\half\sum_i q\ns_i\,\phi(\Bx\ns_i)\quad.\]

Teoría de Debye-H ü ckel

Ahora escribimos la función grand partition:

\[\begin{split} \Xi(T,V,\mu\ns_+,\mu\ns_-)&=\sum_{N\ns_+=0}^\infty\sum_{N\ns_-=0}^\infty {1\over N\ns_+! }\, e^{\beta\mu\ns_+ N\ns_+ }\,\lambda_+^{-N\ns_+ d}\cdot{1\over N\ns_-! }\,e^{\beta\mu\ns_- N\ns_- }\lambda_-^{-N\ns_- d}\\ &\qquad\qquad\cdot\int\!\!d^d\!r\ns_1\cdots\!\int\!\!d^d\!r\ns_{N\ns_+ + N\ns_-}\>e^{-\beta U(\Br\ns_1\,,\,\ldots\,,\,\Br\nd_{N\ns_+ + N\ns_-})}\ . \end{split}\]Ahora adoptamos un enfoque de campo medio, conocido como teoría Debye-H ü ckel, escritura

\[\begin{split} \rho(\Br)&=\rho^{av}(\Br) + \delta\rho(\Br) \\ \phi(\Br)&=\phi^{av}(\Br) + \delta\phi(\Br)\ . \end{split}\]Entonces tenemos

\[\begin{split} U&=\half\!\int\!\!d^d\!r\>\big[\rho^{av}(\Br)+\delta\rho(\Br)\big]\cdot\big[\phi^{av}(\Br) + \delta\phi(\Br)\big]\\ &=\ \stackrel{\equiv\ U\ns_0}{\overbrace{-\half\!\int\!\!d^d\!r\,\rho^{av}(\Br)\,\phi^{av}(\Br) }}+ \int\!\!d^d\!r\>\phi^{av}(\Br)\,\rho(\Br) + \stackrel{\scriptstyle{ignore\ fluctuation\ term}}{\overbrace{ \half\!\int\!\!d^d\!r\,\delta\rho(\Br) \,\delta\phi(\Br)}}\ . \end{split}\]Aplicamos la aproximación media del campo en cada región del espacio, lo que lleva a

\[\begin{split} \Omega(T,V,\mu\ns_+,\mu\ns_-)&=-\kT\lambda_+^{-d}\,z\ns_+\!\int\!\!d^d\!r\,\exp\!\bigg(\!-{e\,\phi^{av}(\Br)\over\kT}\bigg)\\ &\qquad\qquad-\kT\lambda_-^{-d}\,z\ns_-\!\int\!\!d^d\!r\,\exp\!\bigg(\!+{e\,\phi^{av}(\Br)\over\kT}\bigg)\ , \end{split}\]donde

\[\lambda\ns_\pm=\bigg({2\pi\hbar^2\over m\ns_\pm \kT}\bigg)\qquad,\qquad z\ns_\pm=\exp\!\bigg({\mu\ns_\pm\over\kT}\bigg)\ .\]

Por lo tanto, la densidad de carga es

\[\rho(\Br)={\delta\Omega\over\delta\phi^{av}(\Br)}=e\,\lambda_+^{-d}\,z\ns_+\,\exp\!\bigg(\!-{e\,\phi(\Br)\over\kT}\bigg)- e\,\lambda_-^{-d}\,z\ns_-\,\exp\!\bigg(\!+{e\,\phi(\Br)\over\kT}\bigg)\ ,\]donde ahora hemos dejado caer el superíndice\(\phi^{av}(\Br)\) por conveniencia. En\(r\to\infty\), asumimos cargo neutralidad y\(\phi(\infty)=0\). Así

\[\lambda_+^{-d}\,z\ns_+=n\ns_+(\infty)=\lambda_-^{-d}\,z\ns_-=n\ns_-(\infty)\equiv n\ns_\infty \ ,\]donde\(n\ns_\infty\) está la densidad iónica de cualquiera de las especies al infinito. Por lo tanto,

\[\rho(\Br)=-2e\,n\ns_\infty \sinh\!\bigg({e\,\phi(\Br)\over\kT}\bigg)\ .\]Ahora invocamos la ecuación de Poisson,

\[\nabla^2\phi=8\pi e n\ns_\infty \sinh(\beta e\phi) - 4\pi\rho\ns_{ext}\ ,\]donde\(\rho\ns_{ext}\) es una densidad de carga impuesta externamente.

Si\(e\phi\ll\kT\), podemos ampliar la\(\sinh\) función y obtener

\[\nabla^2\phi=\kappa_{\ssr{D}}^2\,\phi-4\pi\rho\ns_{ext}\ ,\]donde

\[\kappa\ns_{\ssr{D}}=\bigg({8\pi n\ns_\infty e^2\over\kT}\bigg)^{\!1/2}\qquad,\qquad \lambda\ns_{\ssr{D}}=\bigg({\kT\over 8\pi n\ns_\infty e^2}\bigg)^{\!1/2}\ .\]La cantidad\(\lambda\ns_{\ssr{D}}\) se conoce como longitud de cribado Debye. Consideremos, por ejemplo, una carga puntual\(Q\) ubicada en el origen. Luego resolvemos la ecuación de Poisson en el límite de campo débil,

\[\nabla^2\phi=\kappa_{\ssr{D}}^2\,\phi-4\pi Q\,\delta(\Br)\ .\]Transformación de Fourier, obtenemos

\[-\Bq^2\,{\hat\phi}(\Bq)=\kappa_{\ssr{D}}^2\,{\hat\phi}(\Bq) - 4\pi Q\qquad\Longrightarrow\qquad {\hat\phi}(\Bq)={4\pi Q\over \Bq^2 + \kappa_{\ssr{D}}^2}\ .\]Transformándonos de nuevo al espacio real, obtenemos, en tres dimensiones, el potencial Yukawa,

\[\phi(\Br)=\int\!\!{d^3\!q\over (2\pi)^3}\,{4\pi Q\,e^{i\Bq\cdot\Br}\over \Bq^2 + \kappa_{\ssr{D}}^2}={Q\over r}\cdot e^{-\kappa\ns_{\ssr{D}} r}\ .\]Esta solución debe descomponerse suficientemente cerca de\(r=0\), ya que el supuesto ya no\(e\phi(r)\ll\kT\) es válido ahí. Sin embargo, para mayores\(r\), la forma Yukawa es cada vez más precisa.

Para otro ejemplo, considere un electrolito retenido entre dos placas conductoras, una a potencial\(\phi(x=0)=0\) y otra a potencial\(\phi(x=L)=V\), donde\(\xhat\) es normal al plano de las placas. De nuevo asumiendo un campo débil\(e\phi\ll\kT\), resolvemos\(\nabla^2\phi=\kappa_{\ssr{D}}^2\,\phi\) y obtenemos

\[\phi(x)=A\,e^{\kappa\ns_{\ssr{D}} x} + B\,e^{-\kappa\ns_{\ssr{D}}\,x}\ .\]Fijamos las constantes\(A\) e\(B\) invocando las condiciones de contorno, lo que resulta en

\[\phi(x)=V\cdot{\sinh(\kappa\ns_{\ssr{D}} x)\over\sinh(\kappa\ns_{\ssr{D}} L)}\ .\]

La teoría de Debye-H ü ckel es válida proporcionada\(n\ns_\infty\,\lambda_{\ssr{D}}^3\gg 1\), por lo que se justifica el supuesto estadístico de muchos cargos en un volumen de tamizaje.

El gas de electrones: tamizaje Thomas-Fermi

Asumiendo\(\kT\ll \veF\), las fluctuaciones térmicas no son importantes y podemos asumir\(T=0\). En el mismo espíritu que el enfoque Debye-H ü ckel, asumimos un potencial electrostático medio que varía lentamente\(\phi(\Br)\). Localmente, podemos escribir

\[\veF={\hbar^2 k_{\ssr{F}}^2\over 2m} - e\phi(\Br)\ .\]Así, el evector de ondas Fermi\(\kF\) es espacialmente variable, de acuerdo con la relación

\[\kF(\Br)=\bigg[{2m\over\hbar^2}\Big(\veF+e\phi(\Br)\Big)\bigg]^{1/2}\ .\]

La densidad del número de electrones local es

\[n(\Br)={k^3_{\ssr{F}}(\Br)\over 3\pi^2}=n\ns_\infty\bigg(1+{e\phi(\Br)\over\veF}\bigg)^{3/2}\ .\]

En presencia de una carga de fondo positiva compensadora uniforme\(\rho\ns_+=e n\ns_\infty\), la ecuación de Poisson toma la forma

\[\nabla^2\phi=4\pi e\,n\ns_\infty\cdot\left[ \bigg(1+{e\phi(\Br)\over\veF}\bigg)^{\!3/2}-1\right]-4\pi\rho\ns_{ext}(\Br)\ .\]

Si\(e\phi\ll\veF\), podemos expandirnos en poderes del ratio, obteniendo

\[\nabla^2\phi={6\pi n\ns_\infty e^2 \over\veF}\,\phi\equiv \kappa_{\ssr{TF}}^2\,\phi-4\pi\rho\ns_{ext}(\Br)\ . \label{KTF}\]

Aquí,\(\kappa\ns_{TF}\) está el evector de ondas Thomas-Fermi,

\[\kappa\ns_{\ssr{TF}}=\bigg({6\pi n\ns_\infty e^2 \over\veF}\bigg)^{\!1/2}\ .\]

La teoría de Thomas-Fermi es válida proporcionada\(n\ns_\infty\,\lambda_{\ssr{TF}}^3\gg 1\), donde\(\lambda\ns_{\ssr{TF}}=\kappa^{-1}_{\ssr{TF}}\), de manera que se justifica la suposición estadística de muchos electrones en un volumen de cribado.

Una aplicación importante del cribado Thomas-Fermi es a la teoría de los metales. En un metal, los electrones exteriores de valencia de cada átomo son despojados del núcleo iónico cargado positivamente y entran en estados itinerantes, similares a ondas planas. Estos estados se dispersan con alguna\(\ve(\Bk)\) función (que es periódica en la zona Brillouin, debajo\(\Bk\to\Bk+\BG\), donde\(\BG\) hay un vector reticular recíproco), y en\(T=0\) esta banda de energía se llena hasta el nivel Fermi\(\veF\), como dicta la estadística de Fermi. (En algunos casos, puede haber varias bandas a nivel Fermi, como vimos en el caso del itrio). El conjunto de núcleos iónicos actúa entonces como un fondo positivo neutralizante. En un cristal perfecto, los núcleos iónicos se distribuyen periódicamente, y el fondo positivo es aproximadamente uniforme. Una impureza cargada en un metal, como un átomo de zinc en una matriz de cobre, tiene una carga nuclear diferente y una valencia diferente a la del huésped. La carga del núcleo iónico, cuando los electrones de valencia son despojados, difiere de la de los iones huésped, y por lo tanto la impureza actúa como impureza de carga local. Por ejemplo, el cobre tiene una configuración electrónica de\([{Ar}]\, 3d^{10}\,4s^{1}\). El\(4\Rs\) electrón forma una banda de energía que contiene la superficie de Fermi. El zinc tiene una configuración de\([{Ar}]\, 3d^{10}\,4s^{2}\), y en una matriz de Cu el Zn cede sus dos\(4s\) electrones en la banda de\(4s\) conducción, dejando atrás un núcleo\(+2\) iónico de carga. Los núcleos de Cu tienen carga\(+1\) ya que cada átomo de cobre aportó solo un\(4s\) electrón a la banda de conducción. Los electrones de la banda de conducción neutralizan el fondo positivo uniforme de los núcleos iónicos Cu. Lo que queda es una carga\(Q=+e\) nuclear extra en el sitio Zn, y un electrón de banda de\(4s\) conducción extra. La\(Q=+e\) impureza es, sin embargo, tamizada por los electrones, y a distancias mayores que un radio atómico el potencial que ve un electrón dado debido al núcleo de Zn es de la forma Yukawa,

\[\phi(\Br)={Q\over r}\cdot e^{-\kappa\ns_{\ssr{TF}}r}\ .\]Debemos cuidar, sin embargo, que la dispersión\(\ve(\Bk)\) para la banda de conducción en un metal no sea necesariamente de la forma de electrones libres\(\ve(\Bk)=\hbar^2\Bk^2/2m\). Al orden lineal en el potencial, sin embargo, el cambio en la densidad electrónica local es

\[\delta n(\Br)=e\phi(\Br)\,g(\veF)\ ,\]donde\(g(\veF)\) está la densidad de estados en la energía Fermi. Así, en un metal, deberíamos escribir

\[\begin{split} \nabla^2\phi&=(-4\pi)(- e\,\delta n)\\ &=4\pi e^2 g(\veF)\,\phi = \kappa_{\ssr{TF}}^2\,\phi\ , \end{split}\]donde

\[\kappa\ns_{\ssr{TF}}=\sqrt{4\pi e^2\,g(\veF)\>}\ .\]El valor de\(g(\veF)\) dependerá de la forma de la dispersión. Para bandas balísticas con una masa efectiva\(m^*\), todavía se aplica la fórmula en Ecuación\ ref {KTF}.

El átomo de Thomas-Fermi

Considera un ion formado por un núcleo de carga\(+Ze\) y una nube de electrones de carga\(-Ne\). La carga iónica neta es entonces\((Z-N)e\). Dado que nos interesarán las escalas atómicas, ya no podemos asumir un límite de campo débil y debemos conservar la teoría de cribado no lineal completa, para lo cual

\[\nabla^2\phi(\Br)=4\pi e\cdot{(2m)^{3/2}\over 3\pi^2\hbar^3}\,\Big(\veF + e\phi(\Br)\Big)^{\!3/2}-4\pi Ze\,\delta(\Br)\ .\]

Asumimos una solución isotrópica. Entonces es conveniente definir

\[\veF+e\phi(\Br)={Ze^2\over r}\cdot\xhi(r/r\ns_0)\ ,\]donde aún no\(r\ns_0\) se ha determinado. Como\(r\to 0\) esperamos\(\xhi\to 1\) ya que la carga nuclear es entonces sin apantallar. Entonces tenemos

\[\nabla^2\left\{{Ze^2\over r}\cdot\xhi(r/r\ns_0)\right\}={1\over r_0^2}\,{Ze^2\over r}\,\chi''(r/r\ns_0)\ ,\]

así llegamos a la ecuación de Thomas-Fermi,

\[\xhi''(t)={1\over\sqrt{t}}\>\xhi^{3/2}(t)\ ,\]con\(r=t\,r\ns_0\), siempre que tomemos

\[r\ns_0={\hbar^2\over 2me^2}\,\bigg({3\pi\over 4\sqrt{Z}}\bigg)^{\!2/3}=0.885\,Z^{-1/3}\,a\ns_{\ssr{B}}\ ,\]

donde\(a\ns_{\ssr{B}}={\hbar^2\over me^2}=0.529\,\) Å es el radio de Bohr. La ecuación TF está sujeta a las siguientes condiciones de límite:

Figura\(\PageIndex{1}\): El átomo de Thomas-Fermi consiste en una carga nuclear\(+Ze\) rodeada de\(N\) electrones distribuidos en una nube. El potencial eléctrico\(\phi(\Br)\) que siente cualquier electrón en posición\(\Br\) es tamizado por los electrones dentro de este radio, lo que resulta en un potencial autoconsistente\(\phi(\Br)=\phi_0+(Ze^2/r)\,\xhi(r/r_0)\).

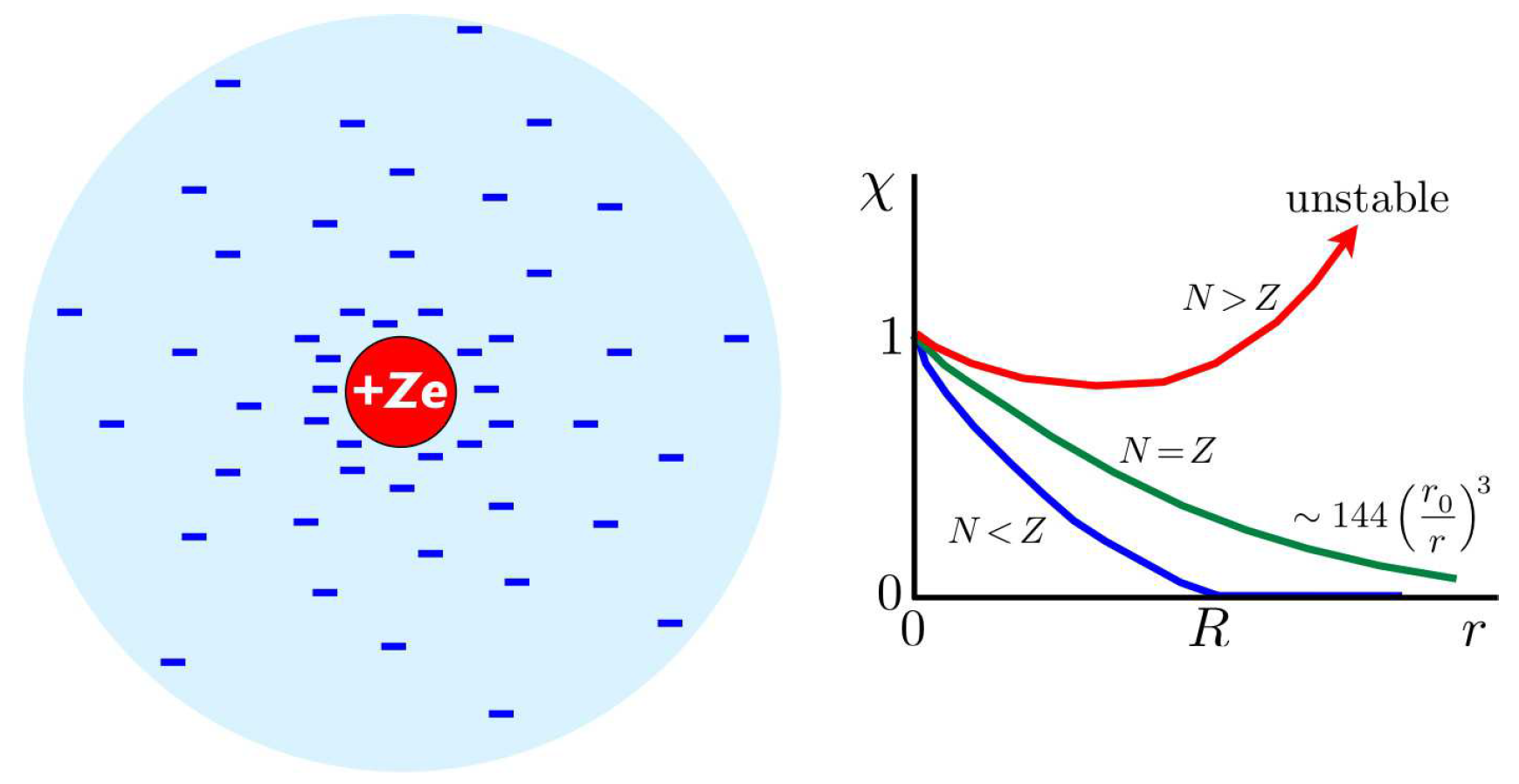
• A distancias cortas, el núcleo está sin apantallar,\[\xhi(0)=1\ .\]
• Para iones positivos, con\(N<Z\), hay cribado perfecto en el límite iónico\(R=t^*\,r\ns_0\), donde\(\xhi(t^*)=0\). Esto requiere\[\BE=-\bnabla\phi=\left[ -{Ze^2\over R^2}\,\xhi(R/r\ns_0) + {Ze^2\over R\,r\ns_0}\,\xhi'(R/r\ns_0)\right]\,\rhat = {(Z-N)\,e\over R^2}\,\rhat\ .\] Esto requiere\[-t^*\,\xhi'(t^*)=1-{N\over Z}\ .\]

Para un átomo, con\(N=Z\), la solución asintótica a la ecuación TF es una ley de poder, y por inspección se encuentra que es\(\xhi(t)\sim C\,t^{-3}\), donde\(C\) es una constante. La constante se desprende de la ecuación TF, que rinde\(12\, C=C^{3/2}\), por lo tanto\(C=144\). Así, un átomo de TF neutro tiene una densidad con una cola de ley de potencia, con\(\rho\sim r^{-6}\). Los iones TF con\(N>Z\) son inestables.