1.1: Introducción - Física estadística y termodinámica

La física estadística (alternativamente llamada “mecánica estadística”) y la termodinámica son dos enfoques diferentes pero relacionados con un mismo objetivo: una descripción aproximada de las ² propiedades “internas” de los grandes sistemas físicos, en particular las que consisten en\(N >> 1\) partículas idénticas, u otros componentes. El ejemplo tradicional de dicho sistema es una porción de gas a escala humana, con el número\(N\) de átomos/moléculas ³ del orden del número Avogadro\(N_A \sim 10^{23}\) (ver Sec. 4 a continuación).

La motivación para el enfoque estadístico de tales sistemas es directa: aunque las leyes que rigen la dinámica de cada partícula y sus interacciones fueran exactamente conocidas, y tuviéramos infinitos recursos informáticos a nuestra disposición, calcular la evolución exacta del sistema en el tiempo sería imposible, al menos porque es completamente impracticable medir el estado inicial exacto de cada componente —en el caso clásico, la posición inicial y la velocidad de cada partícula. La situación se ve agravada aún más por los fenómenos de caos y turbulencia, ⁴ y la incertidumbre cuántico-mecánica, que no permiten el cálculo exacto de las posiciones y velocidades finales de las partículas componentes aunque su estado inicial se conozca con la mejor precisión posible. Como resultado, en la mayoría de las situaciones, solo se pueden hacer predicciones estadísticas sobre el comportamiento de dichos sistemas, convirtiéndose la teoría de la probabilidad en una herramienta importante del arsenal matemático.

Sin embargo, el enfoque estadístico no es tan malo como podría parecer. De hecho, es casi evidente que cualquier variable macroscópica medible que caracterice un sistema estacionario de\(N >> 1\) partículas como un todo (piense, por ejemplo, sobre la presión estacionaria\(P\) del gas contenido en un volumen fijo\(V\)) es casi constante en el tiempo. En efecto, como veremos más adelante, además de ciertas exóticas excepciones, la magnitud relativa de las fluctuaciones —ya sea en el tiempo, o entre muchos sistemas macroscópicamente similares— de tal variable es del orden de\(1/N^{1/2}\), y para\(N \sim N_A\) es extremadamente pequeña. Como resultado, los valores promedio de las variables macroscópicas apropiadas pueden caracterizar bastante bien el estado del sistema, satisfactorios para casi todos los propósitos prácticos. El cálculo de las relaciones entre dichos valores promedio es la única tarea de la termodinámica y la tarea principal de la física estadística. (Las fluctuaciones pueden ser importantes, pero debido a su pequeñez, en la mayoría de los casos su análisis puede basarse en enfoques perturbadores — ver Capítulo 5.)

Ahora echemos un vistazo rápido a las típicas variables macroscópicas con las que deberían operar la física estadística y la termodinámica. Como ya mencioné presión\(P\) y volumen\(V\), permítanme comenzar con este famoso par de variables. En primer lugar, tenga en cuenta que el volumen es una variable extensa, es decir, una variable cuyo valor para un sistema que consta de varias partes que no interactúan es la suma de las de sus partes. Por otro lado, la presión es un ejemplo de una variable intensiva cuyo valor es el mismo para diferentes partes de un sistema —si están en equilibrio—. Para entender por qué\(P\) y\(V\) formar un par natural de variables, consideremos el patio de recreo clásico de la termodinámica, una porción de un gas contenido en un cilindro, cerrado con un pistón móvil de área\(A\) (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Compresión de gas.

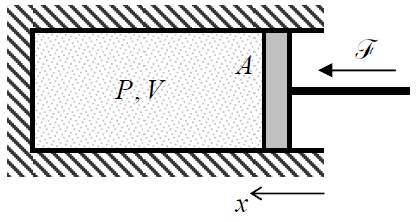
Despreciando la fricción entre las paredes y el pistón, y asumiendo que se está moviendo tan lentamente que la presión\(P\) es prácticamente la misma para todas las partes del volumen en cualquier instante, el trabajo elemental de la fuerza externa\(\mathscr{F} = PA\), comprimiendo el gas, a un pequeño desplazamiento del pistón \(dx = –dV/A\), es

Trabajar en un gas:

\[\boxed{d\mathscr{W} = \mathscr{F}dx = \left(\frac{\mathscr{F}}{A}\right) (Adx) = -PdV.} \label{1}\]

Por supuesto, la última expresión es más general que el modelo mostrado en la Figura\(\PageIndex{1}\), y no depende de la forma particular de la superficie del sistema. ⁵ (Obsérvese que en la notación de Ecuación (\ ref {1}), que se utilizará a través del curso, el trabajo elemental realizado por el gas en el sistema externo es igual\(–d\mathscr{W}\).)

Desde el punto de la mecánica analítica, ⁶\(V\) y\((–P)\) es apenas uno de los muchos pares canónicos posibles de coordenadas generalizadas\(q_j\) y fuerzas generalizadas\(\mathscr{F}_j\), cuyos productos\(d\mathscr{W}_j = \mathscr{F}_jdq_j\) dan contribuciones independientes al trabajo total del entorno sobre el sistema bajo análisis. Por ejemplo, el lector familiarizado con los fundamentos de la electrostática sabe que si la distribución espacial\( \pmb{\mathscr{E}}\mathbf{(r)}\) de un campo eléctrico externo no depende de la polarización eléctrica\(\pmb{\mathscr{P}} \mathbf{(r)}\) de un medio dieléctrico colocado en el campo, su trabajo elemental en el medio es

\[d \mathscr{W}=\int \pmb{\mathscr{E}}(\mathbf{r}) \cdot d \pmb{\mathscr{P}}(\mathbf{r}) d^{3} r \equiv \int \sum_{j=1}^{3} \mathscr{E}_{j}(\mathbf{r}) d \mathscr{P}_{j}(\mathbf{r}) d^{3} r . \label{2a}\]

\[d \mathscr{W}=\sum_{k} d \mathscr{W}_{k}, \quad \text{ with } d \mathscr{W}_{k}=\pmb{\mathscr{E}} \left(\mathbf{r}_{k}\right) \cdot d \pmb{\mathcal{p}}_{k} .\label{2b}\]

\[\begin{align} d \mathscr{W}=\mu_{0} \int \pmb{\mathscr{H}}(\mathbf{r}) \cdot d \pmb{\mathscr{M}}(\mathbf{r}) d^{3} r \equiv \mu_{0} \int \sum_{j=1}^{3} \mathscr{H}_{j}(\mathbf{r}) d \mathscr{M}_{j}(\mathbf{r}) d^{3} r, \label{3a} \\ d \mathscr{W}=\sum_{k} d \mathscr{W}_{k}, \quad \text{ with } d \mathscr{W}_{k}=\mu_{0} \pmb{\mathscr{H}} \left(\mathbf{r}_{k}\right) \cdot d \pmb{\mathcal{m}}_{k} \label{3b}. \end{align} \]

donde\(\pmb{\mathscr{M}}\) y\(\pmb{\mathcal{m}}\) son los vectores de, respectivamente, la magnetización del medio y el momento magnético de un solo dipolo. Las fórmulas (\ ref {2a} -\ ref {2b}) y (\ ref {3a} -\ ref {3b}) muestran que los roles de las coordenadas generalizadas pueden ser desempeñados por componentes cartesianos de los vectores\(\pmb{\mathscr{P}}\) (o\(\pmb{\mathcal{p}}\)) y\(\pmb{\mathscr{M}}\) (o\(\pmb{\mathcal{m}}\)), con los componentes de los campos eléctrico y magnético desempeñando los papeles de los correspondientes fuerzas generalizadas. Esta lista puede extenderse a otras interacciones (como gravitación, tensión superficial en fluidos, etc.). Siguiendo la tradición, usaré el\(\{–P, V \}\) par en casi todas las fórmulas a continuación, pero el lector debería recordar que todas son válidas para cualquier otra pareja\(\{\mathscr{F}_j, q_j\}\). ⁹

Nuevamente, las relaciones específicas entre las variables de cada par enumeradas anteriormente pueden depender de las propiedades estadísticas del sistema bajo análisis, pero sus definiciones no se basan en estadísticas. La situación es muy diferente para un par muy específico de variables, temperatura\(T\) y entropía\(S\), aunque estas “variables hermanas” participan en muchas fórmulas de termodinámica exactamente como si fueran solo un par canónico más\(\{\mathscr{F}_j, q_j\}\). No obstante, la existencia misma de estas dos nociones se debe a las estadísticas. Es decir, la temperatura\(T\) es una variable intensiva que caracteriza el grado de “agitación” térmica de los componentes del sistema. Por el contrario, la entropía\(S\) es una variable extensa que en la mayoría de los casos evade la percepción inmediata por los sentidos humanos; es una medida cualitativa del desorden del sistema, es decir, el grado de nuestra ignorancia sobre su estado microscópico exacto. ¹⁰

La razón de la aparición del\(\{T, S\}\) par de variables en fórmulas de termodinámica y mecánica estadística es que el abordaje estadístico de grandes sistemas de partículas trae algunos resultados cualitativamente nuevos, más notablemente la noción de la evolución temporal irreversible del colectivo ( macroscópicas) que describen el sistema. Por un lado, la irreversibilidad se ve absolutamente natural en fenómenos como la difusión de una gota de tinta en un vaso de agua. Al principio, las moléculas de tinta se ubican en cierta pequeña parte del volumen del sistema, es decir, en cierta medida ordenadas, mientras que en las últimas etapas de difusión, la posición de cada molécula en el vidrio es esencialmente aleatoria. Sin embargo, como segundo pensamiento, la irreversibilidad es bastante sorprendente, teniendo en cuenta que las leyes que rigen el movimiento de los componentes del sistema son reversibles en el tiempo, como las leyes de Newton o las leyes básicas de la mecánica cuántica. ¹¹ En efecto, si en una etapa tardía del proceso de difusión, invertimos las velocidades de todas las moléculas de manera exacta y simultánea, las moléculas de tinta volverían a reunirse (por un momento) en el punto original. ¹² El problema es que no es factible obtener la información necesaria para la inversión exacta de la velocidad. Este ejemplo muestra una profunda conexión entre la mecánica estadística y la teoría de la información.

Una discusión cualitativa del dilema de reversibilidad-irreversibilidad requiere una definición estricta de la noción básica de mecánica estadística (y de hecho de la teoría de la probabilidad), el conjunto estadístico, y me gustaría posponerlo hasta el inicio del Capítulo 2. En particular, en ese capítulo, veremos que la ley básica del comportamiento irreversible es un incremento de la entropía\(S\) en cualquier sistema cerrado. Así, la mecánica estadística, sin desafiar las leyes “microscópicas” que rigen la evolución de los componentes del sistema, introduce sobre ellas algunas nuevas leyes “macroscópicas”, intrínsecamente relacionadas con la evolución de la información, es decir, el grado de nuestro conocimiento del estado microscópico del sistema.

Para concluir esta breve discusión de variables, permítanme mencionar que como en todos los campos de la física, la energía juega un papel muy especial en la mecánica estadística\(E\). Para enfatizar el compromiso de desatender el movimiento del sistema en su conjunto en este subcampo de la física, a lo\(E\) considerado en la termodinámica se le suele llamar la energía interna, aunque sólo por brevedad, me saltaré este adjetivo en la mayoría de los casos. El ejemplo más simple de\(E\) ello es la suma de energías cinéticas de moléculas en un gas diluido en su movimiento térmico, pero en general, la energía interna también incluye no sólo las energías individuales de los componentes del sistema sino también sus interacciones entre sí. Además de algunos casos “patológicos” de interacciones de muy largo alcance, estas interacciones pueden tratarse como locales; en este caso la energía interna es proporcional a\(N\), es decir, es una variable extensa. Como se mostrará a continuación, otras variables extensas con la dimensión de la energía suelen ser muy útiles, incluyendo la energía libre (Helmholtz)\(F\), la energía de Gibbs\(G\), la entalpía\(H\) y el gran potencial\(\Omega\). (El nombre colectivo para tales variables es potenciales termodinámicos.)

Ahora, estamos listos para una breve discusión sobre la relación entre la física estadística y la termodinámica. Si bien la tarea de la física estadística es calcular las variables macroscópicas discutidas anteriormente ¹³ para diversos modelos microscópicos del sistema, el papel principal de la termodinámica es derivar algunas relaciones generales entre los valores promedio de las variables macroscópicas (también llamadas variables termodinámicas) que no dependen de modelos específicos. Sorprendentemente, es posible lograr tal hazaña usando solo unos pocos supuestos generales ya sean evidentes o muy plausibles (a veces llamados las leyes de la termodinámica), que encuentran su prueba en la física estadística. ¹⁴ Tales relaciones generales permiten una reducción sustancial del número de cálculos que tenemos que hacer en la física estadística: en la mayoría de los casos, es suficiente calcular a partir de las estadísticas solo una o dos variables, y luego usar relaciones termodinámicas generales para obtener todas las demás propiedades de interés. Así, la termodinámica, a veces desairada como fenomenología, merece todos los respetos no sólo como una herramienta teórica útil sino también como una disciplina más general que cualquier modelo estadístico particular. Es por ello que el balance de este capítulo está dedicado a una breve revisión de la termodinámica.