2.2: Conjunto microcanónico y distribución

Figura\(\PageIndex{1}\): Imagen muy esquemática del conjunto microcanónico. (En realidad, el conjunto trata de estados cuánticos en lugar de niveles de energía. Un nivel de energía puede ser degenerado, es decir, corresponder a varios estados.)

Este conjunto sirve de base para la formulación del postulado que más frecuentemente se denomina distribución microcanónica (o, más adecuadamente, “el principal postulado estadístico” o “la principal hipótesis estadística”): en el equilibrio termodinámico de un conjunto microcanónico , todos sus estados tienen iguales probabilidades,

Distribución microcanónica:

\[\boxed{ W_m = \frac{1}{M} = \text{const.}} \label{20}\]

Aunque en algunos constructos de mecánica estadística esta igualdad se deriva de otros axiomas, que parecen más plausibles para sus autores, creo que la Ecuación (\ ref {20}) puede tomarse como punto de partida de la física estadística, apoyada “justo” por el cumplimiento de todos sus corolarios con la experimentación observaciones.

Obsérvese que el postulado (\ ref {20}) está estrechamente relacionado con la irreversibilidad macroscópica de los sistemas que son microscópicamente virtualmente reversibles (cerrados): si dicho sistema estaba inicialmente en cierto estado, su evolución temporal con apenas interacciones minúsculas con el ambiente (lo cual es necesario para alcanzar el equilibrio termodinámico) eventualmente conduce a la distribución uniforme de su probabilidad entre todos los estados con esencialmente la misma energía. Cada uno de estos estados no es “mejor” que el inicial; más bien, en un sistema macroscópico, solo hay tantos de estos estados que la posibilidad de encontrar el sistema en el estado inicial es prácticamente nula —de nuevo, piensa en la difusión de gotas de tinta en un vaso de agua. ⁹

Ahora encontremos una definición adecuada de la entropía\(S\) del miembro de un conjunto microcanónico —por ahora, solo en el equilibrio termodinámico—. Esto lo hizo en 1877 otro gigante de la física estadística, Ludwig Eduard Boltzmann —sobre la base del trabajo previo de James Clerk Maxwell sobre la teoría cinética de los gases— ver Sec. 3.1 más adelante. En la terminología actual, dado que\(S\) es una medida de trastorno, debe relacionarse con la cantidad de información ¹⁰ perdida cuando el sistema pasó irreversiblemente del orden completo al trastorno completo, es decir, de un estado definido a la distribución microcanónica (\ ref {20}). En una formulación aún más conveniente, esta es la cantidad de información necesaria para encontrar el estado exacto de su sistema en un conjunto microcanónico.

En la teoría de la información, la cantidad de información necesaria para hacer una elección definitiva entre dos opciones con probabilidades iguales (Figura\(\PageIndex{2a}\)) se define como

\[I (2) \equiv \log_2 2 = 1 \label{21}\]

Esta unidad de información se llama un poco.

Figura\(\PageIndex{2}\): “Árboles logarítmicos” de decisiones binarias para elegir entre (a)\(M = 2\) y (b)\(M = 4\) oportunidades con probabilidades iguales.

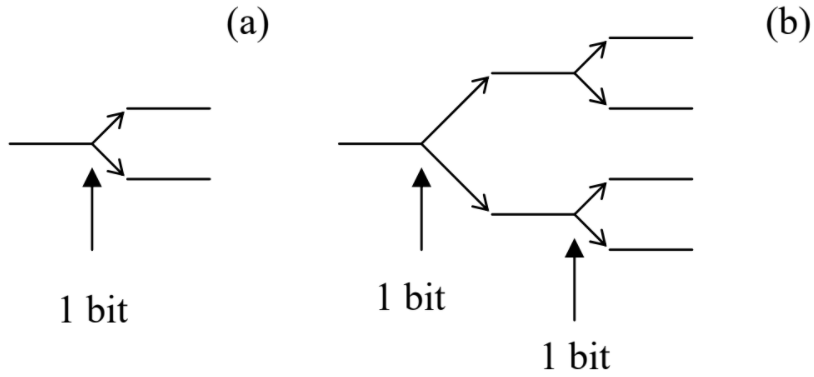
Ahora bien, si necesitamos elegir entre cuatro oportunidades igualmente probables, se puede hacer en dos pasos similares (Figura\(\PageIndex{2b}\)), cada uno requiriendo un bit de información, de manera que la cantidad total de información necesaria para la elección sea

\[I (4) = 2 I (2) = 2 \equiv \log_2 4. \label{22}\]

Una extensión obvia de este proceso a la elección entre\(M = 2^m\) estados da

\[I (M) = mI (2) = m \equiv \log_2 M \label{23}\]

\[ S \equiv \ln M. \label{24a}\]

Usando la ecuación (\ ref {20}), podemos refundir esta definición en su forma más utilizada

Entropía en equilibrio:

\[\boxed{ S = \ln \frac{1}{W_m} = -\ln W_m.} \label{24b}\]

(Nuevamente, tenga en cuenta que la Ecuación (\ ref {24a} -\ ref {24b}) es válida solo en equilibrio termodinámico!)

Nótese que la Ecuación (\ ref {24a} -\ ref {24b}) satisface las principales propiedades de la entropía discutida en la termodinámica. En primer lugar, es una característica única del trastorno. En efecto, según la Ecuación (\ ref {20}),\(M\) (a fijo\(\Delta E\)) es la única medida posible que caracteriza la distribución microcanónica, y también lo es su función única\(\ln M\). Esta función también satisface otro requisito termodinámico a la entropía, de ser una variable extensa. En efecto, para varios sistemas independientes, la probabilidad conjunta de un determinado estado es solo un producto de las probabilidades parciales, y por lo tanto, según la Ecuación (\ ref {24a} -\ ref {24b}), sus entrópías simplemente suman.

Ahora veamos si Eqs. (\ ref {20}) y (\ ref {24a} -\ ref {24b}) son compatibles con la\(2^{nd}\) ley de la termodinámica. Para ello, necesitamos generalizar la Ecuación (\ ref {24a} -\ ref {24b})\(S\) para un estado arbitrario del sistema (generalmente, fuera del equilibrio termodinámico), con un conjunto arbitrario de probabilidades de estado\(W_m\). Primero reconozcamos que\(M\) en la Ecuación (\ ref {24a} -\ ref {24b}) es solo el número de formas posibles de comprometer un sistema particular a un determinado estado\(m\)\((m = 1, 2,...M)\), en un conjunto estadístico donde cada estado es igualmente probable. Ahora consideremos un conjunto más general, que aún consiste en un gran número\(N >> 1\) de sistemas similares, pero con cierto número\(N_m = W_mN >> 1\) de sistemas en cada uno de\(M\) los estados, con los factores\(W_m\) no necesariamente iguales. En este caso, la generalización evidente de la Ecuación (\ ref {24a} -\ ref {24b}) es que la entropía\(S_N\) de todo el conjunto es

\[S_N \equiv \ln M (N_1, N_2 , ...), \label{25}\]

donde\(M (N_1, N_2,...)\) es el número de formas de comprometer un sistema en particular a un determinado estado\(m\) mientras se mantienen\(N_m\) fijos todos los números. Este número\(M (N_1, N_2,...)\) es claramente igual al número de formas de distribuir\(N\) distintas bolas entre\(M\) diferentes cajas, con el número fijo\(N_m\) de bolas en cada caja, pero en ningún orden particular dentro de ella. Comparando esta descripción con la definición de los llamados coeficientes multinomiales, ¹² obtenemos

\[ M\left(N_{1}, N_{2}, \ldots\right)={ }^{N} C_{N_{1}, N_{2}, \ldots, N_{M}} \equiv \frac{N !}{N_{1} ! N_{2} ! \ldots N_{M} !}, \quad \text { with } N=\sum_{m=1}^{M} N_{m} \label{26}\]

Para simplificar la expresión resultante para\(S_N\), podemos usar la famosa fórmula de Stirling, en su forma más cruda, de Moivre, ¹³ cuya precisión es adecuada para la mayoría de los propósitos de la física estadística:

\[ \ln (N!)_{N\rightarrow\infty} \rightarrow N(\ln N-1). \label{27}\]

Cuando se aplica a nuestro problema actual, esta fórmula da la siguiente entropía promedio por sistema, ¹⁴

\[ \begin{align} S & \equiv \frac{S_{N}}{N}=\frac{1}{N}\left[\ln (N !)-\sum_{m=1}^{M} \ln \left(N_{m} !\right)\right]_{N_{m} \rightarrow \infty} \rightarrow \frac{1}{N}\left[N(\ln N-1)-\sum_{m=1}^{M} N_{m}\left(\ln N_{m}-1\right)\right] \nonumber\\ & \equiv-\sum_{m=1}^{M} \frac{N_{m}}{N} \ln \frac{N_{m}}{N} \end{align} \label{28}\]

y como este resultado sólo es válido en el límite de\(N_m \rightarrow \infty\) todos modos, podemos usar Equation (\(2.1.2\)) para representarlo como

Entropía fuera de equilibrio:

\[ \boxed{ S = -\sum^M_{m = 1} W_m \ln W_m = \sum^M_{m=1} W_m \ln \frac{1}{W_m}. } \label{29}\]

Ahora encontremos qué distribución de probabilidades\(W_m\) proporciona el mayor valor de la entropía (\ ref {29}). La respuesta es casi evidente a partir de una buena mirada a la Ecuación (\ ref {29}). Por ejemplo, si para un subgrupo de\(M’ \leq M\) estados los coeficientes\(W_m\) son constantes e iguales a\(1/M’\), de modo que\(W_m = 0\) para todos los demás estados, todos los términos\(M’\) distintos de cero en la suma (\ ref {29}) son iguales entre sí, de modo que

\[S = M' \frac{1}{M'} \ln M' \equiv \ln M',\label{30}\]

y cuanto más\(M’\) cerca de su valor\(M\) máximo, mayor\(S\). De ahí que el máximo de\(S\) se alcance en la distribución uniforme dada por la Ecuación (\ ref {24a} -\ ref {24b}).

Para probar este hecho importante de manera más estricta, encontremos el máximo de la función dada por la Ecuación (\ ref {29}). Si sus argumentos\(W_1, W_2, ...W_M\) fueran completamente independientes, esto podría hacerse encontrando el punto (en el espacio\(M\) -dimensional de los coeficientes\(W_m\)) donde todas las derivadas parciales\(\partial S/\partial W_m\) son iguales a cero. Sin embargo, dado que las probabilidades están limitadas por la condición (\(2.1.4\)), la diferenciación tiene que llevarse a cabo con más cuidado, teniendo en cuenta esta interdependencia:

\[\left[\frac{\partial}{\partial W_{m}} S\left(W_{1}, W_{2}, \ldots\right)\right]_{\text {cond }}=\frac{\partial S}{\partial W_{m}}+\sum_{m^{\prime} \neq m} \frac{\partial S}{\partial W_{m^{\prime}}} \frac{\partial W_{m^{\prime}}}{\partial W_{m}} . \label{31}\]

Al máximo de la función\(S\), todas esas expresiones deben ser iguales a cero simultáneamente. Esta condición rinde\(\partial S/\partial W_m = \lambda \), donde el llamado multiplicador Lagrange\(\lambda\) es independiente de\(m\). De hecho, en tal punto la Ecuación (\ ref {31}) se convierte

\[\left[\frac{\partial}{\partial W_{m}} S\left(W_{1}, W_{2}, \ldots\right)\right]_{\text {cond }}=\lambda+\sum_{m^{\prime} \neq m} \lambda \frac{\partial W_{m^{\prime}}}{\partial W_{m}} \equiv \lambda\left(\frac{\partial W_{m}}{\partial W_{m}}+\sum_{m^{\prime} \neq m} \frac{\partial W_{m^{\prime}}}{\partial W_{m}}\right) \equiv \lambda \frac{\partial}{\partial W_{m}}(1)=0 . \label{32}\]

Para nuestra expresión particular (\ ref {29}), la condición\(\partial S/\partial W_m = \lambda\) rinde

\[\frac{\partial S}{\partial W_{m}} \equiv \frac{d}{d W_{m}}\left[-W_{m} \ln W_{m}\right] \equiv-\ln W_{m}-1=\lambda . \label{33}\]

La última igualdad se mantiene para todos\(m\) (y por lo tanto la entropía alcanza su valor máximo) sólo si\(W_m\) es independiente de\(m\). Así la entropía (\ ref {29}) efectivamente alcanza su valor máximo (\ ref {24a} -\ ref {24b}) en equilibrio.

Para resumir, vemos que la definición estadística (\ ref {24a} -\ ref {24b}) de entropía sí se ajusta a todos los requisitos impuestos a esta variable por la termodinámica. En particular, hemos podido probar la\(2^{nd}\) ley de la termodinámica utilizando esa definición junto con el postulado fundamental (\ ref {20}).

Ahora permítanme discutir un posible punto de incomodidad con esa definición: los valores de\(M\), y por lo tanto\(W_m\), dependen del intervalo energético aceptado\(\Delta E\) del conjunto microcanónico, para cuya elección no se ofrece ninguna orientación exacta. Sin embargo, si el intervalo\(\Delta E\) contiene muchos estados\(M >> 1\), como se suponía antes, entonces con un error relativo muy pequeño (desapareciendo en el límite\(M \rightarrow \infty \)),\(M\) puede representarse como

\[ M = g(E)\Delta E, \label{34}\]

donde\(g(E)\) está la densidad de estados del sistema:

\[g (E) \equiv \frac{d\Sigma (E)}{dE}, \label{35}\]

\(\Sigma (E)\)siendo el número total de estados con energías por debajo\(E\). (Obsérvese que el intervalo promedio\(\delta E\) entre los niveles de energía, mencionado al inicio de esta sección, es justo\(\Delta E/M = 1/g(E)\).) Al enchufar la ecuación (\ ref {34}) en la ecuación (\ ref {24a} -\ ref {24b}), obtenemos

\[ S = \ln M = \ln g(E) + \ln \Delta E, \label{36}\]

de manera que el único efecto de una elección particular de\(\Delta E\) es un desplazamiento de la entropía por una constante, y en el Capítulo 1 hemos visto que tal desplazamiento constante no afecta a ninguna cantidad medible. Por supuesto, la Ecuación (\ ref {34}), y por lo tanto la Ecuación (\ ref {36}) solo son precisas en el límite cuando la densidad de estados\(g(E)\) es tan grande que el rango disponible para la elección apropiada de\(\Delta E\):

\[g^{-1} (E) << \Delta E << E, \label{37}\]

es suficientemente amplio:\(g(E)E = E/\delta E >> 1\).

Para tener alguna idea de las funciones\(g(E)\)\(S(E)\) y la viabilidad de la condición (\ ref {37}), y también para ver si la distribución microcanónica puede ser utilizada directamente para cálculos de variables termodinámicas en sistemas particulares, apliquemos a un conjunto microcanónico de muchos conjuntos de osciladores armónicos\(N >> 1\) independientes y similares con frecuencia\(\omega \). (Tenga en cuenta que el requisito de una energía prácticamente fija se aplica, en este caso, a la energía total\(E_N\) de cada conjunto de osciladores, más bien a la energía\(E\) de un solo oscilador —que puede ser virtualmente arbitraria, aunque ciertamente mucho menor que\(E_N \sim NE >> E\).) La mecánica cuántica básica nos dice ¹⁷ que las energías propias de tal oscilador forman un espectro discreto y equidistante:

\[E_{m}=\hbar \omega\left(m+\frac{1}{2}\right), \text { where } m=0,1,2, \ldots \label{38}\]

Si\(\omega\) se mantiene constante, la energía del estado fundamental\(\hbar \omega /2\) no contribuye a ninguna propiedad termodinámica del sistema, ¹⁸ de manera que en aras de la simplicidad podemos tomar ese punto como el origen de la energía, y reemplazar la Ecuación (\ ref {38}) con\(E_m = m\hbar \omega \). Realicemos un análisis aproximado del sistema para el caso cuando su energía promedio por oscilador,

\[E = \frac{E_N}{N}, \label{39}\]

es mucho más grande que el cuántico de energía\(\hbar \omega \).

Para un oscilador, el número de estados con energía\(\varepsilon_1\) por debajo de cierto valor\(E_1 >> \hbar \omega\) es evidentemente\(\Sigma (E_1) \approx E_1/\hbar \omega \equiv (E_1/\hbar \omega )/1!\) (Figura\(\PageIndex{3a}\)). Para dos osciladores, todos los valores posibles de la energía total\((\varepsilon_1 + \varepsilon_2)\) por debajo de algún nivel\(E_2\) corresponden a los puntos de una cuadrícula cuadrada 2D dentro del triángulo rectángulo que se muestra en la Figura\(\PageIndex{3b}\), dando\(\Sigma (E_2) \approx (1/2)(E_2/\hbar \omega )^2 \equiv (E_2/\hbar \omega )^{2}/2!\). Para tres osciladores, los posibles valores de la energía total\((\varepsilon_1 + \varepsilon_2 + \varepsilon_3)\) corresponden a aquellos puntos de la cuadrícula cúbica 3D, que encajan dentro de la pirámide derecha que se muestra en la Figura\(\PageIndex{3c}\)\(\Sigma (E_3) \approx (1/3)[(1/2)(E_3/\hbar \omega )^3] \equiv (E_3/\hbar \omega )^3/3!\), dando, etc.

Figura\(\PageIndex{3}\): Cálculo de funciones\(\Sigma (E_N)\) para sistemas de (a) uno, (b) dos y (c) tres osciladores armónicos.

Una evidente generalización de estas fórmulas a arbitrarias\(N\) da el número de estados ¹⁹.

\[\Sigma (E_N) \approx \frac{1}{N!} \left( \frac{E_N}{\hbar \omega}\right)^N. \label{40}\]

Diferenciando esta expresión sobre la energía, obtenemos

\[g(E_N) \equiv \frac{d\Sigma (E_N)}{dE_N} = \frac{1}{(N-1)!} \frac{E^{N-1}_{N}}{(\hbar \omega)^N}, \label{41}\]

para que

\[S_N (E_N ) = \ln g(E_N ) + \text{ const } = − \ln [(N −1)!]+ (N −1) \ln E_N − N \ln (\hbar \omega ) + \text{ const}. \label{42}\]

Porque\(N >> 1\) podemos ignorar la diferencia entre\(N\) y\((N – 1)\) en ambas instancias, y usar la fórmula de Stirling (\ ref {27}) para simplificar este resultado como

\[S_{N}(E)-\text { const } \approx N\left(\ln \frac{E_{N}}{N \hbar \omega}+1\right) \approx N\left(\ln \frac{E}{\hbar \omega}\right) \equiv \ln \left[\left(\frac{E} {\hbar \omega}\right)^{N}\right] \label{43}\]

(El segundo paso aproximado solo es válido en\(E/\hbar \omega\) proporciones muy altas, cuando el logaritmo en la Ecuación (\ ref {43}) es sustancialmente mayor que 1.) Volviendo por un segundo a la densidad de estados, vemos que en el límite\(N \rightarrow \infty \), es exponencialmente grande:

\[g(E_N) = e^{S_N} \approx \left(\frac{E}{\hbar \omega} \right)^N, \label{44}\]

para que las condiciones (\ ref {37}) puedan satisfacerse dentro de un rango muy amplio de\(\Delta E\).

Ahora podemos usar la Ecuación (\ ref {43}) para encontrar todas las propiedades termodinámicas del sistema, aunque sólo en el límite\(E >> \hbar \omega \). En efecto, según la termodinámica, si el volumen del sistema y el número de partículas en él son fijos, la derivada no\(dS/dE\) es otra cosa que la temperatura recíproca en equilibrio térmico — ver Ecuación (\(1.2.6\)). En nuestro caso actual, implicamos que los osciladores armónicos son distintos, por ejemplo por sus posiciones espaciales. De ahí que aunque podamos hablar de algún volumen del sistema, ciertamente es fijo. ²⁰ Ecuación diferenciadora (\ ref {43}) sobre la energía\(E\), obtenemos

Oscilador clásico: energía promedio

\[\boxed{\frac{1}{T} \equiv \frac{dS_N}{dE_N} = \frac{N}{E_N} = \frac{1}{E}.} \label{45}\]

Al leer este resultado hacia atrás, vemos que la energía promedio\(E\) de un oscilador armónico es igual\(T\) (es decir,\(k_BT_K\) es unidades SI). En este punto, el estudiante primerizo de termodinámica debería sentirse muy aliviado al ver que la definición termodinámica contra-intuitiva (\(1.2.6\)) de temperatura sí corresponde a lo que todos hemos sabido sobre esta noción desde nuestros cursos de física de jardín de infantes.

El resultado (\ ref {45}) puede generalizarse fácilmente. De hecho, en mecánica cuántica, un oscilador armónico con frecuencia\(\omega\) propia puede ser descrito por el operador hamiltoniano

\[\hat{H} = \frac{\hat{p}^2}{2m}+\frac{\kappa \hat{q}^2}{2},\label{46}\]

donde\(q\) está alguna coordenada generalizada,\(p\) es el momento generalizado correspondiente,\(\mathbf{m}\) es la masa del oscilador, ²¹ y\(\kappa\) es la constante de resorte, así que eso\(\omega = (\kappa /\mathbf{m})^{1/2}\). Dado que en el equilibrio termodinámico la matriz de densidad siempre es diagonal en base a estados estacionarios\(m\) (ver Sec. 1 anterior), los promedios mecánicos cuánticos de las energías cinética y potencial pueden encontrarse en la Ecuación (\(2.1.7\)):

\[\left\langle\frac{p^{2}}{2 \mathbf{m}}\right\rangle=\sum_{m=0}^{\infty} W_{m}\left\langle m\left|\frac{\hat{p}^{2}}{2 \mathbf{m}}\right| m\right\rangle, \quad\left\langle\frac{\kappa q^{2}}{2}\right\rangle=\sum_{m=0}^{\infty} W_{m}\left\langle m\left|\frac{\kappa \hat{q}^{2}}{2}\right| m\right\rangle \label{47}\]

donde\(W_m\) es la probabilidad de ocupar el nivel de\(m^{th}\) energía, y los vectores bra y ket describen el estado estacionario correspondiente a ese nivel. ²² Sin embargo, tanto la mecánica clásica como la cuántica nos enseñan que para cualquiera\(m\), las expresiones bra-ket bajo las sumas en Eqs. (\ ref {47}), que representan las energías cinéticas y mecánicas promedio del oscilador en su nivel de\(m^{th}\) energía, son iguales entre sí, y por lo tanto cada una de ellas es igual a\(E_m/2\). De ahí que a pesar de que\(W_m\) aún no conocemos la distribución de probabilidad (se calculará en la Sec. 5 a continuación), podemos concluir que en el “límite clásico”\(T >> \hbar \omega \),

\[\boxed{ \left\langle\frac{p^{2}}{2 \mathbf{m}}\right\rangle= \left\langle\frac{\kappa q^{2}}{2}\right\rangle = \frac{T}{2}.} \label{48}\]

\[\hat{H} = \sum_j \hat{H}_j, \quad \text{with } \hat{H}_j = \frac{\hat{p}^2_j}{2\mathbf{m}_j} + \frac{\kappa_j \hat{q}^2_j}{2}, \label{49}\]

con frecuencias (generalmente, diferentes)\(\omega_j = (\kappa_j/\mathbf{m}_j)^{1/2}\). Dado que los “modos” (osciladores armónicos efectivos) que contribuyen a este hamiltoniano, son independientes, el resultado (\ ref {48}) es válido para cada uno de los modos. Este es el famoso teorema de equipartición: en equilibrio térmico con\(T >> \hbar \omega_j\), la energía promedio de cada uno de los llamados medios grados de libertad (que se define como cualquier variable, ya sea\(p_j\) o\(q_j\), dando una contribución cuadrática al hamiltoniano del sistema), es igual a \(T/2\). ²⁴ En particular, para cada una de las tres contribuciones de componentes cartesianos a la energía cinética de una partícula de movimiento libre, este teorema es válido para cualquier temperatura, ya que tales componentes pueden considerarse como osciladores armónicos 1D con energía potencial de fuga, es decir\(\omega_j = 0\), así esa condición\(T >> \hbar \omega_j\) se cumple a cualquier temperatura.

Creo que este estudio de caso de sistemas de osciladores armónicos fue una clara ilustración tanto de las fortalezas como de las debilidades del enfoque de ensamble microcanónico. ²⁵ Por un lado, podríamos calcular fácilmente prácticamente todo lo que queríamos en el límite clásico\(T >> \hbar \omega \), pero los cálculos para una arbitraria\(T \sim \hbar \omega \), aunque posible, son bastante desagradables porque para eso, todos los pasos verticales de la función\(\Sigma (E_N)\) tienen que ser contados cuidadosamente. En la Sec. 4, veremos que otros conjuntos estadísticos son mucho más convenientes para tales cálculos.

Permítanme concluir esta sección con un breve aviso sobre los sistemas clásicos deterministas con apenas unos pocos grados de libertad (e incluso objetos matemáticos más simples llamados “mapas”) que pueden exhibir un comportamiento esencialmente desordenado, llamado el caos determinista. ²⁶ Tal sistema caótico puede caracterizarse aproximadamente por una entropía definida de manera similar a la Ecuación (\ ref {29}), donde\(W_m\) están las probabilidades de encontrarlo en diferentes regiones pequeñas del espacio de fase, a intervalos de tiempo pequeños bien separados. Por otro lado, se puede utilizar una expresión ligeramente más general que la Ecuación (\ ref {29}) para definir la llamada entropía Kolmogorov (o “Kolmogorov-Sinai”)\(K\) que caracteriza la velocidad de pérdida de la información sobre el estado inicial del sistema, y de ahí lo que es llamado la “profundidad del caos”. En la definición de\(K\), la suma sobre\(m\) se sustituye por la suma sobre todas las posibles permutaciones\(\{m\} = m_0, m_1, ..., m_{N-1}\) de pequeñas regiones espaciales, y\(W_m\) se sustituye por\(W_{\{m\}}\), la probabilidad de encontrar el sistema en las regiones correspondientes m en el momento del tiempo\(t_m\), con \(t_m = m\tau \), en el límite\(\tau \rightarrow 0\), con\(N\tau =\) const. Para el caos en los objetos más simples, los mapas 1D,\(K\) es igual al exponente Lyapunov\(\lambda > 0\). ²⁷ Para los sistemas de mayor dimensionalidad, que se caracterizan por varios exponentes de Lyapunov\(\lambda \), la entropía de Kolmogorov es igual al promedio fase-espacio de la suma de todos los positivos\(\lambda \). Estos hechos proporcionan una forma mucho más practicable de cálculo (típicamente, numérico) de la entropía de Kolmogorov que el uso directo de su definición. ²⁸