9.1: Tutorial de Matemáticas — Ondas Complejas

Hasta ahora hemos representado ondas planas mecánicas cuánticas por funciones sinusoidales y coseno, al igual que con otros tipos de ondas. Sin embargo, las ondas de materia plana no pueden ser verdaderamente representadas por senos y cosenos. En cambio, necesitamos funciones matemáticas en las que el desplazamiento de las olas sea complejo y no real. Esto requiere la introducción de un poco de nuevas matemáticas, que abordamos primero. Usando nuestra nueva herramienta matemática, podemos explorar dos ideas de importancia crucial en la mecánica cuántica; (1) la relación entre la simetría y las leyes de conservación, y (2) la dinámica de las ondas espacialmente confinadas.

Un número complejo\(z\) es la suma de un número real y un número imaginario. Un número imaginario es solo un número real multiplicado por\(i \equiv(-1)^{1 / 2}\). Así, podemos escribir\(z=a+i b\) para cualquier complejo\(z\), dónde\(a\) y\(b\) son reales. Las cantidades\(a\) y\(b\) son las partes reales e imaginarias de\(z\), a veces escritas\(Re(z)\) y\(Im(z)\).

La mecánica cuántica requiere que las funciones de onda sean complejas, es decir, poseer partes reales e imaginarias. Las ondas planas en la mecánica cuántica en realidad toman la forma\(\Psi=\exp [\mathrm{i}(\mathrm{kx}-\omega \mathrm{t})]\) en lugar de, digamos,\(\cos (k x-\omega t)\). La razón de esto es la necesidad de distinguir entre ondas con frecuencias positivas y negativas. Si reemplazamos\(k\) y\(\omega\) con\(-\mathrm{k}\) y\(-\omega\) en forma de coseno, obtenemos

\[\cos (-k x+\omega t)=\cos [-(k x-\omega t)]=\cos (k x-\omega t).\]

En otras palabras, cambiar el signo de\(k\) y no da como\(\omega\) resultado ningún cambio en una onda expresada como una función coseno. Los dos estados mecánicos cuánticos, uno con número de onda y frecuencia\(\mathrm{k}\)\(\omega\) y el otro con\(-\mathrm{k}\) y\(-\omega\), producen funciones de onda indistinguibles y por lo tanto representarían estados físicamente indistinguibles. Por lo tanto, la forma coseno es insuficientemente flexible para representar ondas mecánicas cuánticas. Por otro lado, si reemplazamos k y ω con sus negativos en la forma exponencial compleja de una onda plana obtenemos\(\psi=\exp [-\mathrm{i}(\mathrm{kx}-\omega \mathrm{t})]\), que es diferente de\(\exp [\mathrm{i}(\mathrm{kx}-\omega \mathrm{t})]\). Estas dos funciones de onda son distinguibles y, por lo tanto, corresponden a distintos estados físicos.

No es inmediatamente obvio que una función exponencial compleja proporciona el comportamiento oscilatorio necesario para representar una onda plana. Sin embargo, el exponencial complejo se puede expresar en términos de senos y cosenos usando la ecuación de Euler:

\[\exp (i \phi)=\cos (\phi)+i \sin (\phi) \quad \text { (Euler's equation). }\label{9.1}\]

Figura 9.1: Representación gráfica de un número complejo z como punto en el plano complejo. Los componentes cartesianos horizontales y verticales dan las partes real e imaginaria de z respectivamente.

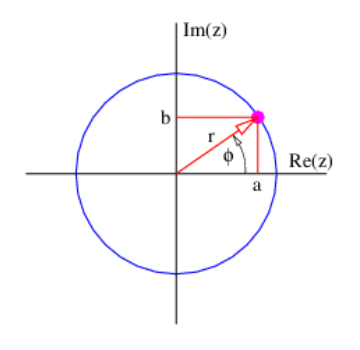
Si definimos\(r=\left(a^{2}+b^{2}\right)^{1 / 2} \text { and } \phi=\tan ^{-1}(b / a)\), entonces una forma alternativa de expresar un número complejo es z = r exp (iϕ), que por la ecuación de Euler es igual\(r \cos (\phi)+\operatorname{ir} \sin (\phi)\). La comparación lo demuestra\(\mathrm{a}=r \cos (\phi) \text { and } \mathrm{b}=r \sin (\phi)\). Así, un número complejo puede considerarse como un punto en el plano a-b con las coordenadas cartesianas a y b y las coordenadas polares r y\(\phi\). El plano a-b se llama el plano complejo.

Ahora vemos cómo la función de onda compleja representa una oscilación. Si\(\Psi=\exp [\mathrm{i}(\mathrm{kx}-\omega \mathrm{t})]\), la función compleja\(\psi(x, t)\) se mueve alrededor y redondea el círculo unitario en el plano complejo a medida que x y t cambian, como se ilustra en la figura 9.1. Esto contrasta con la oscilación de ida y vuelta a lo largo del eje horizontal del plano complejo representado por\(\cos (\mathrm{kx}-\omega \mathrm{t})\).

No presentaremos una prueba formal de la ecuación de Euler —eventualmente la verás en tu curso de cálculo. Sin embargo, puede ser útil señalar que las\(\phi\) derivadas de\(\exp (\text { iф })\) y\(\cos (\phi)+\mathrm{i} \sin (\phi)\) tienen el mismo comportamiento:

\[\begin{align} \frac{d}{d \phi} \exp (i \phi) &=i \exp (i \phi)\label{9.2}\\[4pt] \frac{d}{d \phi}[\cos (\phi)+i \sin (\phi)] &=-\sin (\phi)+i \cos (\phi) \\[4pt] &=i[\cos (\phi)+i \sin (\phi)]. \label{9.3}\end{align}\]

(En la segunda de estas ecuaciones hemos sustituido el signo menos frente a la función sinusoidal por\(\mathrm{i}^{2}\) y luego hemos extraído un factor común de i.) La\(\phi\) derivada de ambas funciones devuelve así la función de nuevo veces i. Esto es un fuerte indicio que\(\exp (\mathrm{i} \phi) \text { and } \cos (\phi)+\mathrm{i} \sin (\phi)\) son diferentes formas de representar la misma función.

Indicamos el conjugado complejo de un número complejo z mediante un asterisco superíndice, i. e.,\(\mathrm{z}^{*}\). Se obtiene sustituyendo i por -i. Por lo tanto,\((a+i b)^{*}=a-i b\). El cuadrado absoluto de un número complejo es el número multiplicado por su conjugado complejo:

\[|z|^{2}=|a+i b|^{2} \equiv(a+i b)(a-i b)=a^{2}+b^{2}=r^{2}\label{9.4}\]

Observe que el cuadrado absoluto de una función exponencial compleja es uno:

\[|\exp (i \phi)|^{2}=\exp (i \phi) \exp (-i \phi)=\exp (i \phi-i \phi)=\exp (0)=1\label{9.5}\]

En mecánica cuántica el cuadrado absoluto de la función de onda en cualquier punto expresa la probabilidad relativa de encontrar la partícula asociada en ese punto. Así, la probabilidad de encontrar una partícula representada por una onda plana es uniforme en el espacio. Contraste esto con la probabilidad relativa asociada a una onda sinusoidal:\(|\sin (k x-\omega t)|^{2}=\sin ^{2}(k x-\omega t)\). Esto varía de cero a uno, dependiendo de la fase de la onda. La “ondulación” en una onda plana exponencial compleja reside en la fase más que en la magnitud de la función de onda.

Se necesita una pieza más de matemáticas. El complejo conjugado de la ecuación de Euler es

\[\exp (-i \phi)=\cos (\phi)-i \sin (\phi)\label{9.6}\]

Tomando la suma y la diferencia de esto con la ecuación original de Euler da como resultado la expresión del seno y el coseno en términos de exponenciales complejos:

\[\cos (\phi)=\frac{\exp (i \phi)+\exp (-i \phi)}{2} \quad \sin (\phi)=\frac{\exp (i \phi)-\exp (-i \phi)}{2 i}\label{9.7}\]

No estamos acostumbrados a que aparezcan números complejos en las teorías físicas y es difícil imaginar cómo mediríamos tal número. Sin embargo, todo lo observable proviene de tomar el cuadrado absoluto de una función de onda, por lo que tratamos solo con números reales en experimentos.