9.4: Problemas

1. Supongamos que una partícula está representada por la función de onda\(\Psi=\sin (\mathrm{kx}-\omega \mathrm{t})+\sin (-\mathrm{kx}-\omega \mathrm{t})\).
   1. Utilice la trigonometría para simplificar esta función de onda.
   2. Compute la dependencia x y t de la probabilidad de encontrar la partícula al cuadrar la función de onda.
   3. Explique lo que dice este resultado sobre la dependencia temporal de la probabilidad de encontrar la partícula. ¿Tiene sentido esto?
2. Repita el problema anterior para una partícula representada por la función de onda\(\Psi=\exp [\mathrm{i}(\mathrm{kx}-\omega \mathrm{t})]+\exp [\mathrm{i}(-\mathrm{kx}-\omega \mathrm{t})]\).
3. Determinar si la función de onda\(\psi(x)=\exp \left(i C x^{2}\right)\) es invariante bajo desplazamiento en el sentido de que la función de onda desplazada difiere de la función de onda original por solo un factor de fase.
4. Así como la invarianza bajo la sustitución\(x \rightarrow x+D\) se asocia con el impulso, la invarianza bajo la sustitución\(x \rightarrow-x\) se asocia con una variable mecánica cuántica llamada paridad, denotada\(P\). Sin embargo, a diferencia del impulso, que puede tomar cualquier valor numérico, la paridad puede tomar sólo dos valores posibles,\(\pm 1\). La paridad de una función de onda\(\Psi(x) \text { is }+1 \text { if } \Psi(-x)=\psi(x)\), mientras que la paridad es\(-1 \text { if } \Psi(-\mathrm{x})=-\Psi(\mathrm{x}) . \text { If } \Psi(\mathrm{x})\) satisface ninguna de estas condiciones, entonces no tiene un valor definido de paridad.
   1. ¿Cuál es la paridad\(\Psi=\sin (\mathrm{kx}) ? \text { Of } \Psi=\cos (\mathrm{kx})\)? La cantidad k es una constante.
   2. ¿Es\(\psi(x)=\cos (k x)\) invariante bajo la sustitución x = x + D para todos los valores posibles de D? ¿Esta función de onda tiene un valor definido del impulso?
   3. Demostrar que una función de onda con un valor definido del impulso no tiene un valor definido de paridad. ¿Las variables de impulso y paridad son compatibles?
5. Al darse cuenta de que se\(\cos (k x-\omega t)\) puede escribir en términos de funciones exponenciales complejas, dar una interpretación física del significado de la función de onda coseno anterior. En particular, ¿cuáles son los posibles valores del impulso y la energía de la partícula asociada?
6. La operación de inversión de tiempo T realiza la sustitución\(\mathrm{t} \rightarrow-\mathrm{t}\). Similar a la paridad, la inversión del tiempo solo puede tomar valores\(\pm 1\). ¿La simetría de una onda funciona bajo inversión de tiempo, es decir\(\text { i. e., } \psi(-t)=\Psi(t)\), consistente con un valor definido de la energía? Pista: Cualquier función de onda correspondiente a un valor definido de energía E debe tener la forma\(\Psi=A \exp (-\mathrm{iEt} / \hbar)\) donde A no es una función del tiempo t. (¿Por qué?)
7. La operación C toma el complejo conjugado de la función de onda, es decir, realiza la sustitución\(\mathrm{i} \rightarrow-\mathrm{i}\). En la mecánica cuántica moderna esto corresponde a partículas y antipartículas intercambiables, y se llama conjugación de carga. ¿Qué le hace la operación combinada CPT a una onda plana compleja, es decir, una con vector de onda definido y frecuencia?
8. Hacer un diagrama de nivel de energía para el caso de una partícula sin masa en una caja.
9. Compare |π| para el estado fundamental de una partícula no relativista en una caja de tamaño a con Δπ obtenido del principio de incertidumbre en esta situación. Pista: ¿Para qué deberías tomar\(\Delta \mathrm{x}\)?
10. Imagina que una mesa de billar tiene un borde infinitamente alto a su alrededor. Para este problema supongamos que\(\hbar=1 \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}\).
    1. Si la mesa mide 1.5 m de largo y si la masa de una bola de billar es M = 0.5 kg, ¿cuál es la energía más baja o baja de la bola de billar? Pista: A pesar de que la mesa de billar es bidimensional, trata esto como un problema unidimensional. También, tratar el problema de manera no relativista e ignorar la contribución de la energía de descanso a la energía total.
    2. La energía requerida para levantar la bola sobre un borde de altura H contra la gravedad es\(\mathrm{U}=\mathrm{MgH} \text { where } \mathrm{g}=9.8 \mathrm{~m} \mathrm{~s}^{-2}\). Qué altura de llanta hace que la energía potencial gravitacional sea igual a la energía del estado del suelo de la bola de billar calculada anteriormente.
    3. Si la llanta es en realidad dos veces más alta que la calculada anteriormente pero es solo 0. 1 m de grosor, determinar la probabilidad de que la pelota penetre en el borde. 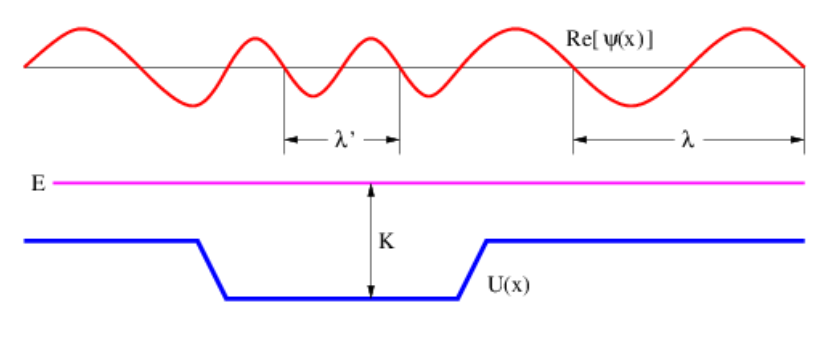Figura 9.7: Parte real de la función de onda ψ, correspondiente a una energía total fija E, que ocurre en una región de energía potencial espacialmente variable\(\mathrm{U}(\mathrm{x})\). Observe cómo\(\lambda\) cambia la longitud de onda a medida que\(\mathrm{K}=\mathrm{E}-\mathrm{U}\) cambia la energía cinética.
11. La parte real de la función de onda de una partícula con energía positiva E que pasa por una región de energía potencial negativa se muestra en la figura 9.7.
    1. Si la energía total es definitivamente E, ¿cuál es la dependencia de esta función de onda en el tiempo?
    2. ¿La función de onda es invariante bajo desplazamiento en el espacio en este caso? ¿Por qué o por qué no?
    3. ¿Esta función de onda corresponde a un valor definido de impulso? ¿Por qué o por qué no?
    4. ¿El impulso es compatible con la energía en este caso? ¿Por qué o por qué no?
12. Suponiendo de nuevo eso\(\hbar=1 \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}\), ¿cuáles son las velocidades posibles de un tren de juguete de masa 3 kg que discurre alrededor de una vía circular de radio 0.8 m?
13. Si una partícula de masa cero que se desliza alrededor de un bucle circular de radio R puede tomar momentos angulares\(\mathrm{L}_{\mathrm{m}}=\mathrm{m} \hbar\) donde\(m\) está un número entero, ¿cuáles son las posibles energías cinéticas de la partícula? Pista: Recuerda eso\(\mathrm{L}=\Pi \mathrm{R}\).