9.3: Ondas de materia confinada
- Page ID
- 125962
El confinamiento de una onda a una región espacial limitada da como resultado un comportamiento bastante peculiar: la onda solo puede encajar cómodamente en la región confinada si la frecuencia de onda, y por lo tanto la energía de partícula asociada, adquiere un conjunto limitado de valores posibles. Este es el origen de la famosa cuantificación de la energía, de la que proviene el “cuántico” en la mecánica cuántica. Exploraremos dos tipos de confinamiento, confinamiento de posición debido a un pozo de energía potencial y confinamiento rotacional debido a que la rotación de un objeto a través de\(2π\) radianes devuelve el objeto a su orientación original.
Partícula en una caja
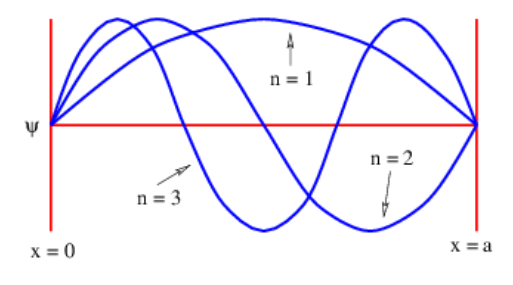
Ahora imaginamos cómo debe comportarse una partícula confinada a una región\(0 \leq x \leq a\) en el eje x. Al igual que con el desplazamiento de una cuerda de guitarra, la función de onda debe ser cero en\(x = 0\) y a, es decir, en los extremos de la cuerda de guitarra. Una sola onda plana exponencial compleja no puede satisfacer esta condición, ya que\(|\exp [\mathrm{i}(\mathrm{kx}-\omega \mathrm{t})]|^{2}=1\) en todas partes. Sin embargo, una superposición (con un signo menos) de ondas viajeras hacia la izquierda y hacia la derecha crea una onda estacionaria, en la que la función de onda se separa en una función del espacio sola multiplicada por una función del tiempo solo.
\[\psi=\exp [i(k x-\omega t)]-\exp [i(-k x-\omega t)]=2 i \exp (-i \omega t) \sin (k x)\label{9.13}\]
Observe que la dependencia del tiempo sigue siendo un exponencial complejo, lo que significa que\(|\Psi|^{2}\) es independiente del tiempo. Esto asegura que la probabilidad de encontrar la partícula en algún lugar de la caja permanece constante con el tiempo. También significa que el paquete de ondas corresponde a una energía definida\(\mathrm{E}=\hbar \omega\).
Debido a que tomamos una diferencia más que una suma de ondas planas, la condición ya\(\psi=0\) está satisfecha en\(x = 0\). Para satisfacerlo en\(x=a\), debemos tener\(\mathrm{ka}=\mathrm{n} \pi\), donde\(\mathrm{n}=1,2,3, \ldots\). Así, el valor absoluto del número de onda debe tomar los valores discretos
\[k_{n}=\frac{n \pi}{a}, \quad n=1,2,3, \ldots\label{9.14}\]
(Los números de onda de las dos ondas planas son iguales a más o menos este valor absoluto respectivamente). Esto implica que el valor absoluto del momento de la partícula es\(\Pi_{n}=\hbar \mathrm{k}_{\mathrm{n}}=\mathrm{nr} \hbar \mathrm{a}\), lo que a su vez significa que la energía de la partícula debe ser
\[E_{n}=\left(\Pi_{n}^{2} c^{2}+m^{2} c^{4}\right)^{1 / 2}=\left(n^{2} \pi^{2} \hbar^{2} c^{2} / a^{2}+m^{2} c^{4}\right)^{1 / 2}\label{9.15}\]
donde m es la masa de partículas. En el límite no relativista esto se convierte en
\[E_{n}=\frac{\Pi_{n}^{2}}{2 m}=\frac{n^{2} \pi^{2} \hbar^{2}}{2 m a^{2}} \quad \text { (non-relativistic) }\label{9.16}\]
donde hemos bajado la energía de descanso\(\mathrm{mc}^{2}\) ya que es un desplazamiento constante. En el caso ultrarrelativista donde podemos ignorar la masa de partículas, encontramos
\[E_{n}=\left|\Pi_{n}\right| c=\frac{n \pi \hbar c}{a} \quad \text { (zero mass) }\label{9.17}\]
Las formas de las funciones de onda para los tres primeros valores de\(n\) para la partícula en el cuadro se ilustran en la figura 9.2.
En ambos límites la energía toma solo un cierto conjunto de valores posibles. Esto se llama cuantificación de energía y el entero n se llama el número cuántico de energía. En el límite no relativista la energía es proporcional a\(n^{2}\), mientras que en el caso ultrarrelativista la energía es proporcional a n.
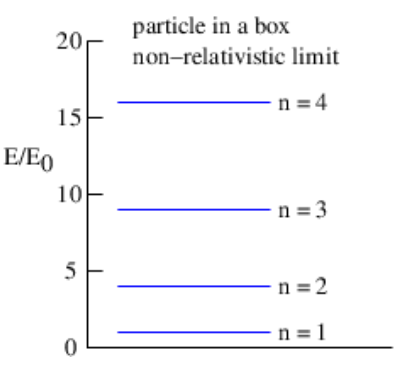
Podemos representar gráficamente los niveles de energía permitidos para la partícula en una caja mediante un diagrama de niveles de energía. Dicho diagrama se muestra en la Figura 9.3 para el caso no relativista.
Un aspecto de este problema merece una mirada más cercana. La ecuación (\ ref {9.13}) muestra que la función de onda para este problema es una superposición de dos ondas planas correspondientes a momenta\(\Pi_{1}=+\hbar \mathrm{k} \text { and } \Pi_{2}=-\hbar \mathrm{k}\) y por lo tanto es una especie de paquete de ondas. Así, la función de onda no es invariante bajo desplazamiento y no corresponde a un valor definido del impulso —el valor absoluto del impulso es definido, pero su signo no lo es. Siguiendo la prescripción de Feynman, la ecuación (\ ref {9.13}) nos dice que la amplitud para que la partícula en la caja tenga impulso\(+\hbar \mathrm{k} \text { is } \exp [\mathrm{i}(\mathrm{kx}-\omega \mathrm{t})]\), mientras que la amplitud para que tenga impulso\(-\hbar k \text { is }-\exp [\mathrm{i}(-\mathrm{kx}-\omega \mathrm{t})]\). El cuadrado absoluto de la suma de estas amplitudes nos da la probabilidad relativa de encontrar la partícula en la posición x:
\[P(x)=|2 i \exp (-i \omega t) \sin (k x)|^{2}=4 \sin ^{2}(k x)\label{9.18}\]
Cuál de los dos posibles valores del impulso que adquiere la partícula es incognoscible, así como es imposible en principio saber por qué hendidura pasa una partícula en dos rendijas de interferencia. Si se realiza un experimento para medir el momento, entonces la función de onda se cambia irreversiblemente, así como el patrón de interferencia en el problema de las dos rendijas se destruye si la hendidura a través de la cual pasa la partícula se determina inequívocamente.
Penetración de barrera
A diferencia de la situación en la mecánica clásica, la mecánica cuántica permite que la energía cinética K sea negativa. Esto hace que el impulso\(\Pi\left(\right.\text { equal to }(2 \mathrm{mK})^{1 / 2}\) en el caso no relativista) imaginario, lo que a su vez da lugar a un número de onda imaginario.
Investiguemos la naturaleza de una ola con un número de onda imaginario. Supongamos que\(\mathrm{k}=\mathrm{i} \kappa\) en una onda plana exponencial compleja, donde\(\kappa\) es real:
\[\psi=\exp [i(k x-\omega t)]=\exp (-\kappa x-i \omega t)=\exp (-\kappa x) \exp (-i \omega t)\label{9.19}\]
La función de onda no oscila en el espacio cuando\(\mathrm{K}=\mathrm{E}-\mathrm{U}<0\), sino que crece o decae exponencialmente con x, dependiendo del signo de\(\kappa\).
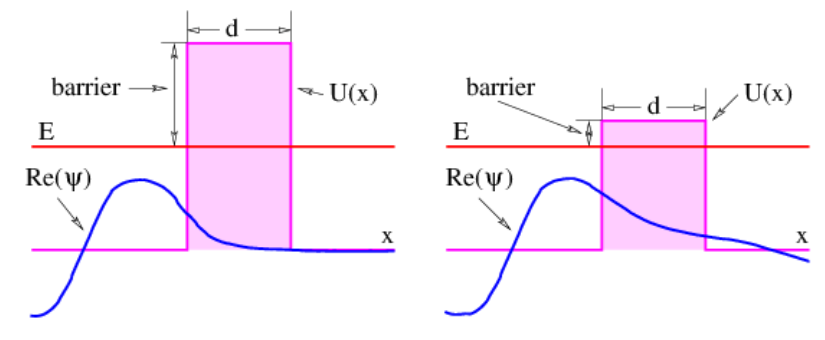
Para una partícula que se mueve hacia la derecha, con positivo\(k\) en la región permitida,\(\kappa\) resulta ser positiva, y la solución se descompone hacia la derecha. Así, una partícula que incide sobre una barrera de energía potencial desde la izquierda (es decir, mientras se mueve hacia la derecha) tendrá su decaimiento de amplitud de onda en la región clásicamente prohibida, como se ilustra en la figura 9.4. Si esta descomposición es muy rápida, entonces el resultado es casi indistinguible del resultado clásico —la partícula no puede penetrar en gran medida en la región prohibida. Sin embargo, si la descomposición es lenta, entonces hay una probabilidad razonable de encontrar la partícula en la región prohibida. Si la región prohibida es finita en extensión, entonces la amplitud de onda será pequeña, pero distinta de cero en su límite derecho, lo que implica que la partícula tiene una probabilidad finita de pasar completamente por la región prohibida clásica. Este proceso se llama penetración de barrera.
La probabilidad de que una partícula penetre en una barrera es el cuadrado absoluto de la amplitud después de la barrera dividido por el cuadrado de la amplitud antes de la barrera. Así, en el caso de la función de onda ilustrada en la ecuación (\ ref {9.19}), la probabilidad de penetración es
\[P=|\psi(d)|^{2} /|\psi(0)|^{2}=\exp (-2 \kappa d)\label{9.20}\]
donde d es el grosor de la barrera.
La tasa de decaimiento exponencial con x en la región prohibida está relacionada con lo negativo que es K en esta región. Desde
\[-K=U-E=-\frac{\Pi^{2}}{2 m}=-\frac{\hbar^{2} k^{2}}{2 m}=\frac{\hbar^{2} \kappa^{2}}{2 m}\label{9.21}\]
encontramos que
\[\kappa=\left(\frac{2 m B}{\hbar^{2}}\right)^{1 / 2}\label{9.22}\]
donde está la barrera energética potencial\(B \equiv-K=U-E\). Cuanto menor es B, menor es\(\kappa\), lo que resulta en una disminución menos rápida de la función de onda con x, lo que corresponde a una penetración de barrera más fuerte. (Obsérvese que la forma en que se define B, es positiva en regiones prohibidas.)
Si la barrera de energía es muy alta, entonces la decadencia exponencial de la función de onda es muy rápida. En este caso la función de onda va casi a cero en el límite entre las regiones permitidas y prohibidas. Es por ello que especificamos que la función de onda sea cero en las paredes para la partícula en una caja. Estos muros actúan en efecto como barreras de potencial infinitamente alto.
La penetración de barrera es importante en una serie de fenómenos naturales. Ciertos tipos de desintegración radiactiva y la fisión de núcleos pesados se rigen por este proceso.
Momento angular orbital
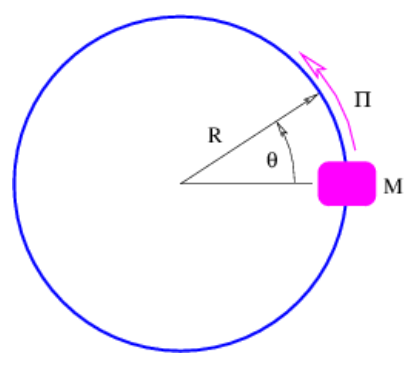
Otro tipo de movimiento de estado enlazado ocurre cuando una partícula está restringida para moverse en un círculo. (Imagine un reborde deslizándose sobre un lazo circular de alambre, como se ilustra en la figura 9.5.) Podemos definir x en este caso como la longitud del camino alrededor del cable y relacionarlo con el\(\text { angle } \theta: x=\operatorname{R\theta}\). Para una ola de avión tenemos
\[\psi=\exp [i(k x-\omega t)]=\exp [i(k R \theta-\omega t)]\label{9.23}\]
Esta onda plana difiere de la onda plana normal para el movimiento a lo largo de un eje cartesiano en que debemos tener\(\psi(\theta)=\psi(\theta+2 \pi)\). Esto sólo puede suceder si la circunferencia del bucle,\(2 \pi \mathrm{R}\), es un número integral de longitudes de onda, es decir, si\(2 \pi \mathrm{R} / \lambda=\mathrm{m}\) donde m es un número entero. Sin embargo, ya que\(2 \Pi / \lambda=\mathrm{k}\), esta condición se vuelve\(\mathrm{kR}=\mathrm{m}\).
Ya que\(\Pi=\hbar k\), se puede escribir la condición anterior\(\Pi_{m} R=m \hbar\). La cantidad
\[L_{m} \equiv \Pi_{m} R\label{9.24}\]
se llama el momento angular, lo que lleva a nuestro resultado final,
\[L_{m}=m \hbar, \quad m=0,\pm 1,\pm 2, \ldots\label{9.25}\]
Vemos que el momento angular solo puede tomar valores que son múltiplos enteros de. Esto representa la cuantificación del momento angular, y m en este caso se denomina número cuántico de momento angular. Tenga en cuenta que este número cuántico difiere del número cuántico de energía para la partícula en la caja en que se permiten valores cero y negativos.
La energía de nuestra cuenta en un bucle de alambre se puede expresar en términos del momento angular:
\[E_{m}=\frac{\Pi_{m}^{2}}{2 M}=\frac{L_{m}^{2}}{2 M R^{2}}\label{9.26}\]
Esto significa que el momento angular y la energía son variables compatibles en este caso, lo que significa además que el momento angular es una variable conservada. Así como los valores definidos de impulso lineal están relacionados con la invarianza bajo traslaciones, los valores definidos de momento angular están relacionados con la invarianza bajo rotaciones. Así, tenemos
\[\text { invariance under rotation } \Longleftrightarrow \text { definite angular momentum }\label{9.27}\]
para el momento angular.
Tenemos que abordar brevemente el tema del momento angular en tres dimensiones. El momento angular es en realidad un vector orientado perpendicular al bucle de alambre en el ejemplo que estamos discutiendo. La dirección del vector se define usando una variación en la regla de la derecha: Enrilla tus dedos en la dirección del movimiento del cordón alrededor del bucle (¡usando tu mano derecha!). La orientación del vector de momento angular se define por la dirección en la que apunta el pulgar. Esto te dice, por ejemplo, que el momento angular en la figura 9.5 señala fuera de la página.
En mecánica cuántica solo es posible medir simultáneamente el cuadrado de la longitud del vector de momento angular y un componente de este vector. Dos componentes diferentes del momento angular no se pueden medir simultáneamente debido al principio de incertidumbre. Sin embargo, la longitud del vector de momento angular puede medirse simultáneamente con un componente. Así, en la mecánica cuántica, el momento angular se especifica completamente si se conoce la longitud y una componente del vector de momento angular.
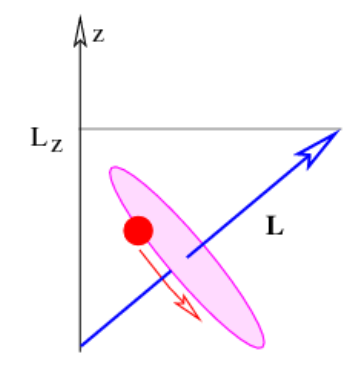
La Figura 9.6 ilustra el vector de momento angular asociado con una perla que se mueve sobre un bucle de alambre que se inclina desde la horizontal. También se muestra un componente (tomado como el componente z). Por razones que no podemos explorar aquí, el cuadrado de la longitud del vector de momento angular L 2 se cuantifica con los siguientes valores:
\[L_{l}^{2}=\hbar^{2} l(l+1), \quad l=0,1,2, \ldots\label{9.28}\]
Un componente (digamos, el componente z) del momento angular se cuantifica igual que el momento angular en el caso bidimensional, excepto que l actúa como límite superior sobre los posibles valores de\(|\mathrm{m}|\). En otras palabras, si el cuadrado de la longitud del vector de momento angular es\(\hbar^{2} \mid(\mid+1)\), entonces el componente z puede tomar los valores
\[L_{z m}=\hbar m, \quad m=-l,-l+1, \ldots, l-1, l\label{9.29}\]
A la cantidad l se le llama número cuántico de momento angular, mientras que m se denomina número cuántico de orientación o magnético, este último por razones históricas.
Momento angular
El tipo de momento angular discutido anteriormente está asociado con el movimiento de partículas en órbitas. Sin embargo, resulta que incluso las partículas estacionarias pueden poseer un momento angular. Esto se llama momento angular de giro. El número cuántico de espín s juega un papel análogo al\(l\) del momento angular de giro, es decir, el cuadrado del vector de momento angular de giro de una partícula es
\[L_{s}^{2}=\hbar^{2} s(s+1)\label{9.30}\]
El número cuántico de orientación de espín m s está relacionado de manera similar con s:
\[L_{z s}=\hbar m_{s}, \quad m_{s}=-s,-s+1, \ldots, s-1, s\label{9.31}\]
El momento angular de giro para una partícula elemental está absolutamente conservado, es decir, nunca puede cambiar. Así, el valor de s es una propiedad intrínseca de una partícula. La principal diferencia entre el giro y el momento angular orbital es que el número cuántico de espín puede tomar más valores, es decir,\(s=0,1 / 2,1,3 / 2,2,5 / 2, \ldots\)
Las partículas con valores de espín entero\(\mathrm{s}=0,1,2, \ldots\) se llaman bosones después del físico indio Satyendra Nath Bose. Las partículas con valores de espín medio entero\(s=1 / 2,3 / 2,5 / 2, \ldots\) se llaman fermiones después del físico italiano Enrico Fermi. Como veremos más adelante en el curso, los bosones y los fermiones juegan papeles muy diferentes en el universo.


