12.6: Problemas

Última actualización
Guardar como PDF

Page ID: 126048

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Un oscilador (no armónico) tiene la función de energía potencial\(\mathrm{U}(\mathrm{x})=\mathrm{Cx}^{4}\), donde C es una constante. ¿Cómo depende la frecuencia de oscilación de la energía? Explica tu razonamiento.
Demostrar que\(\mathrm{C} \cos (\omega \mathrm{t}-\phi)\) es una forma alternativa de escribir\(A \sin (\omega t)+B \cos (\omega t)\) encontrando los valores de A y B en términos de las constantes\(\mathrm{C} \text { and } \phi\). Pista: Expandir\(\cos (\omega t-\phi)\) usando la identidad trigonométrica para el coseno de la suma de dos ángulos.
Si un oscilador armónico masa-resorte tiene desplazamiento\(x=0\) y velocidad\(\mathrm{dx} / \mathrm{dt}=\mathrm{V}\) en el tiempo\(\mathrm{t}=0\), determine los valores de A y B así como los de C y\(\phi\) en la ecuación (12.2.4).
Una masa M se suspende contra la gravedad por un resorte de constante de resorte k. La longitud no estirada del resorte es\(\mathrm{x}_{0}\) y bajo la influencia de la gravedad el resorte se estira a una longitud de reposo\(x_{1}>x_{0}\).
1. Calcular la longitud del resorte x ₁ en el estuche estable y en reposo.
2. Establecer la ecuación de movimiento para la masa que se mueve bajo la influencia de las dos fuerzas, la gravedad y la primavera. Resolver la ecuación para la frecuencia de la oscilación y la posición del resorte en función del tiempo x (t). ¿La frecuencia de oscilación cambia de la caja sin gravedad?
Determinar las dos soluciones reales al problema del oscilador armónico amortiguado en el caso en el que\(\omega_{0}^{2}<\beta^{2}\). 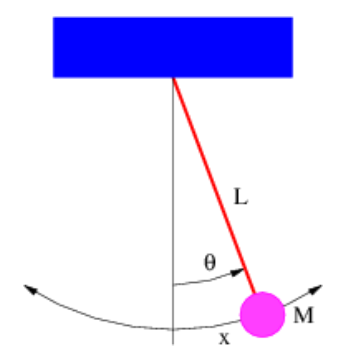Figura 12.5: El péndulo como oscilador armónico.
Considera el péndulo en la figura 12.5. La masa M se mueve a lo largo de un arco con x denotando la distancia a lo largo del arco desde el punto de equilibrio.
1. Encontrar el componente de la fuerza gravitacional tangente al arco (y así en la dirección del movimiento de la masa) en función del ángulo\(theta\). Utilice la aproximación de ángulo pequeño\(\sin (\theta)\) para simplificar esta respuesta.
2. Obtener la fuerza en términos de x en lugar de\(\theta\). (Recordemos eso\(\theta=x / L\).)
3. Utilice la segunda ley de Newton para el movimiento en la dirección x (es decir, a lo largo del arco seguido de la masa) para obtener la ecuación de movimiento para la masa.
4. Resuelve la ecuación de movimiento usando como guía la solución al problema masa-resorte.
Oscilador amortiguado forzado:
1. Agregue un término de amortiguación a la ecuación del oscilador armónico forzado (12.3.1) y resuelva para la parte forzada de la solución usando métodos exponenciales complejos. Pista: Cambiar el coseno del lado derecho de esta ecuación\(\exp \left(i \omega_{F} t\right)\) para convertir la ecuación a forma compleja y luego probar la solución\(x=x_{0} \exp \left(i \omega_{F} t\right)\) donde\(\mathrm{x}_{0}\) dependerá de\(\omega_{F}\). También, escribir la ecuación en términos de\(\beta=b /(2 M) \text { and } \omega^{2}=k / M\).
2. Encuentra la parte física de esta solución tomando la parte real de x (t). Pista: Si bien se toma la parte real de x, puede ser útil recordar que se puede escribir la inversa de cualquier número complejo\(1 /(a+i b)=(a-i b) /\left(a^{2}+b^{2}\right)\).
3. Determinar en qué\(\mathrm{x}_{0}\) se diferencia de eso en el caso sin amortiguar cuando\(\omega_{F}\) está cerca de la frecuencia resonante del oscilador no forzado. En particular, mostrar cómo la fase y amplitud de la oscilación cambian a medida que la frecuencia de forzamiento cambia de menor a mayor que la frecuencia resonante.
Una partícula sin masa está confinada a una caja de longitud a. (Piense en un fotón entre dos espejos). Tratando la partícula clásicamente, computar el periodo de un viaje de ida y vuelta de un extremo de la caja al otro y de regreso. A partir de esto se calcula una frecuencia angular para la oscilación de esta partícula en la caja. ¿Esta frecuencia depende de la energía de la partícula?
Calcular la energía\(\mathrm{E}_{\text {ground }}\) del estado fundamental de una partícula sin masa en una caja de longitud a usando mecánica cuántica. Comparar\(\mathrm{E}_{\text {ground }} / \hbar\) con la frecuencia angular calculada en el problema anterior.