7.7: Brillo
- Page ID
- 90147
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Básico
El brillo es el grado de “brillo” de una piedra preciosa, resultante de la luz reflejada y refractada de las facetas de la corona y del pabellón. La brillantez es una percepción visual global basada en las leyes físicas de la refracción y la reflexión.

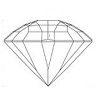
Figura\(\PageIndex{1}\): Reflejo Interno Total en un Diamante. La luz que llega a la faceta en un ángulo mayor que el ángulo crítico se reflejará.
Cuando la luz incide sobre la superficie de un medio transparente ópticamente más denso (como una piedra preciosa) se reflejará desde la superficie (rebotada) o parcialmente refractada (doblada y enviada en otra dirección) dentro de la piedra. Cuando se refracta un rayo de luz, choca con una faceta de pabellón y o bien se refracta fuera de la piedra o se refleja dentro de la piedra dependiendo de qué ángulo el rayo de luz se acerca a la faceta (Fig.1, ver su explicación a continuación).
Cada piedra tiene un ángulo en el que el rayo de luz será refractado (enviado a lo largo de un camino diferente) o reflejado (rebotado). Este ángulo se conoce como el ángulo crítico y depende del índice de refracción de la piedra (cuánto se dobla el rayo de luz). Cuanto mayor sea el índice de refracción, menor será el ángulo crítico.
Cuando un rayo de luz se acerca a una faceta de pabellón en un ángulo mayor que el ángulo crítico, se reflejará completamente dentro de la piedra. Lo contrario dicta que la luz que cae en un ángulo menor que el ángulo crítico será refractada fuera de la piedra. Esta propiedad es muy importante en la confección de una piedra preciosa para crear brillantez o “vida”. Como cada piedra preciosa tiene su propio ángulo crítico, el diseño del corte debe ajustarse para la piedra en cuestión.
Explicación de la Figura\(\PageIndex{1}\): En este ejemplo se muestra un Diamante de talla brillante, que tiene un ángulo crítico (“ca”) de aproximadamente 24°26' (24 grados y 26 minutos). El camino que recorre la luz (la línea azul) es el siguiente:
- la luz llega a la corona de la piedra y se refracta (dobla) dentro de la piedra, doblándose hacia el punto número 2
- el rayo de luz alcanza una faceta de pabellón en un ángulo mayor que el ángulo crítico (ca), por lo que se reflejará (rebotará) hacia 3
- en el punto 3, el rayo de luz vuelve a llegar a la faceta del pabellón en un ángulo mayor que el ángulo crítico por lo que se reflejará hacia 4
- aquí, el rayo de luz llega a la corona en un ángulo que es menor que el ca, por lo que será refractado fuera de la piedra
El ángulo crítico se mide a partir de una línea imaginaria llamada normal (NO). Esta línea se dibuja a 90° con respecto a la superficie de la faceta en el punto donde la luz alcanza esa faceta.
En una piedra transparente bien proporcionada, toda la luz que ingrese a la piedra facetada a través de la corona quedará atrapada dentro de la piedra por un tiempo y luego será refractada fuera de la piedra a través de la corona. Este comportamiento se conoce como Reflexión Interna Total (a menudo abreviado como TIR) y es el ingrediente clave en el diseño de un refractómetro. Cabe señalar que este fenómeno único solo ocurre en los límites de un medio ópticamente más denso (piedra preciosa) y un medio ópticamente más raro (como el aire) cuando la luz viaja dentro del medio más denso.
Cuando una piedra transparente está mal cortada (ya sea con un pabellón demasiado poco profundo o demasiado profundo), la luz saldrá por el pabellón. La luz que sangra a través de las facetas del pabellón hace que una piedra aparezca demasiado clara o demasiado oscura. El brillo se basa mucho en la transparencia, por lo tanto, las piedras con buena transparencia mostrarán mejor brillo cuando se corten bien.
Por supuesto, en las piedras preciosas de colores, otros factores como la zonificación del color, el pleocroísmo, etc. también juegan un papel en la decisión de cómo se necesita cortar una piedra para obtener el mejor rendimiento óptico.
Avanzado
\[critical\ angle = \arcsin \left (\frac {1}{n}\right )\ \Rightarrow \ critical\ angle = \arcsin \left ( \frac {1}{2.417}\right )\ \approx\ 24^\circ26'\]
Figura\(\PageIndex{2}\): Relación entre ángulo crítico e índice de refracción
El ángulo crítico se puede calcular como el Seno inverso de 1 dividido por n (el índice de refracción) de una piedra preciosa. Para Diamante con n = 2.417, el cálculo será el seno inverso de 1/2.417 (donde 1 es el índice de refracción del aire).
Nota: la fórmula real es arcsin (n2/n1), pero como nosotros los gemólogos generalmente solo nos preocupamos por el ángulo crítico entre el aire y la gema, n2 = 1.
A partir de la fórmula del ángulo crítico, se hace evidente la relación entre el índice de refracción de una piedra preciosa y el ángulo crítico. Cuanto mayor sea el índice de refracción, menor será el ángulo crítico.