7.15: Doble refracción
- Page ID
- 90072
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Algunas piedras preciosas tienen más de un índice de refracción (RI) debido a que estas piedras pertenecen a sistemas cristalinos (anisotrópicos) que tienen estructuras atómicas que provocan que un rayo de luz incidente se resuelva en dos rayos que viajan a diferentes velocidades. Esta diferencia relacionada con las velocidades se denomina “birrefringencia”. Cuando los dos rayos cambian su dirección de desplazamiento (es decir, son refractados) y se mueven en diferentes direcciones este fenómeno se llama “doble refracción. La diferencia numérica entre un valor de RI y el otro valor de RI medido en cualquier caso se denomina “birrefringencia” para esa prueba, y la diferencia entre el RI más alto posible y el menor RI posible considerando todas las direcciones posibles se denomina birrefringencia de la piedra preciosa.
La refracción es cuando la luz cambia de dirección a medida que pasa a través de una superficie. La refringencia es cuando la luz cambia de velocidad a medida que pasa a través de una superficie. La luz que pasa a través de una superficie en la normalidad puede ser ralentizada sin ser refractada. La luz que pasa a través de una superficie con inclinación permite que la desaceleración de esa luz cambie la dirección de desplazamiento, produciendo refracción. Los materiales birrefringentes ralentizan la luz a dos velocidades diferentes (según cada una de las dos direcciones de vibración mutuamente perpendiculares). Cuando la luz viaja a un circón a través de la cara prisma de un cristal, las vibraciones se clasifican en dos y cada vibración viaja a una velocidad diferente. Si la luz entra en un ángulo oblicuo, cada vibración cambia de dirección y viaja a lo largo de caminos que difieren de la trayectoria original Y difieren entre sí. Se trata de una doble refracción causada por la birrefringencia. Si la luz entra normal a la cara del prisma, cada vibración viaja a una velocidad diferente, pero no se produce refracción. Ambas vibraciones fueron incidentes en una perpendicular al frente de onda por lo que el cambio de velocidad no provoca un cambio de dirección. En esta dirección, la luz experimenta cero refracción y birrefringencia máxima.
Básico

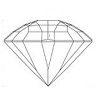
Figura\ (\ PageIndex {1} |): Rayo incidente separado en un rayo ordinario (ω) y un rayo extra-ordinario (ε)
Cuando un rayo de luz entra en la piedra preciosa, la estructura atómica permite que solo continúen aquellos rayos que vibran en dos direcciones específicas.
Estos dos rayos vibran en planos que son mutuamente perpendiculares y por lo tanto están polarizados. Ambos rayos viajan a diferentes velocidades dentro de la piedra preciosa y así se refractarán en diferentes ángulos cuando incidan distintos a los paralelos a lo normal.
La fuerza de birrefringencia (BI) varía con la dirección y medimos el BI máximo (Δ).
Estos valores máximos difieren de una piedra preciosa a otra. Por ejemplo:
- BI Fuerte - circón (0.059)
- Medio BI - turmalina (0.020)
- BI bajo - cuarzo (0.009)
En las piedras preciosas uniaxiales, un rayo vibrará en la dirección perpendicular al eje óptico y obedecerá la Ley de Snell (se puede calcular su ángulo de refracción). Este rayo se llama el rayo ordinario (generalmente indicado con ω). El otro rayo vibra perpendicular a la vibración del primer rayo y en una dirección entre perpendicular y paralela al eje óptico (generalmente con cierta inclinación) y así no obedece a la Ley de Snell (es decir, el ángulo de refracción variará según el ángulo de vibración). Ese rayo se llama el rayo extra-ordinario (indicado por ε).
La diferencia máxima de RI entre estos dos rayos se denomina “birrefringencia”, a menudo indicada por el símbolo “Δ” (letra griega delta). Esta diferencia es mayor cuando la luz ingresa a la piedra preciosa en un ángulo perpendicular al eje óptico. Cuando la luz ingresa a la gema en un ángulo paralelo al eje óptico, la birrefringencia será 0 (cero).
Si bien en gemología el término “birrefringencia” suele indicar la diferencia máxima entre los rayos ordinarios y extraordinarios (o las lecturas α y γ en piedras biaxiales), el término también se aplica a cualquier variación en los índices de refracción. No sólo el máximo.
En las piedras facetadas, una fuerte birrefringencia puede resultar en la duplicación visual de las facetas, lo que se observa en una gran cantidad de circones. Aunque el BI está en su máximo cuando se ve en la dirección perpendicular al eje óptico, no se verá duplicación de facetas en esa dirección debido a la superposición.
Cuando se examina una piedra anistópica en dirección paralela a un eje óptico, la piedra se comportará como una piedra preciosa istropica. Por lo tanto tampoco se verá duplicación de facetas en esa dirección.
Las piedras preciosas pertenecientes al sistema de cristales cúbicos y las gemas amorfas tienen solo un RI y por lo tanto no muestran birrefringencia; todas las demás piedras preciosas sí.
Las piedras uniaxiales (las que cristalizan en los sistemas trigonal, hexagonal y tetragonal) mostrarán dos lecturas y tendrán un eje óptico.
Las piedras preciosas biaxiales (sistemas ortorrómbico, monoclínico y triclínico) tienen dos direcciones en las que la luz incidente reaccionará como si fuera isotrópica y por lo tanto tendrán dos ejes ópticos.
Temas relacionados
Fuentes
- Richard H. Cartier - Una nueva definición de ejes ópticos para gemología y los cuatro tipos de ejes ópticos, The Journal of Gemmology, Vol. 29 no.4 (octubre 2004) pp. 228 - 234
- Richard H. Cartier - Revista de Gemología, 2003, Vol. 28, núm. 8, pp. 489-493
- Richard H. Cartier - Revista de Gemología, 2002, Vol. 28, núm. 4, pp. 223-226
- Gemología 3ª edición (2005) - Peter Read