11.1: Fuerzas mareales

Nuestra comprensión moderna de la formación de mareas proviene de la Ley de Gravitación Universal de Isaac Newton, que establece que dos objetos cualesquiera tienen una atracción gravitacional el uno hacia el otro. La magnitud de la fuerza es proporcional a las masas de los objetos, e inversamente proporcional al cuadrado de la distancia entre los objetos, según la ecuación de la Figura\(\PageIndex{1}\).

Figura Ley de la Gravitación Universal de\(\PageIndex{1}\) Newton. La fuerza gravitacional entre dos objetos (F) se calcula como el producto de las dos masas (m ₁ y m ₂) divididas por la distancia entre ellos (r) al cuadrado. G es la constante gravitacional universal; 6.67408 × 10 ^-11 m ³ kg ^-1 s ^-2 (By I, Dennis Nilsson [CC BY 3.0], vía Wikimedia Commons).

En el caso de las mareas, hay algunos otros factores que modifican esta ecuación para que la distancia (r) sea cúbica en lugar de cuadrada, dando a la distancia un impacto aún mayor en las fuerzas mareales. Pero para nuestros propósitos, la lección importante es que cuanto mayores son las masas de los objetos, mayor es la fuerza gravitacional, y cuanto más lejos están los objetos unos de otros, más débil es la fuerza.

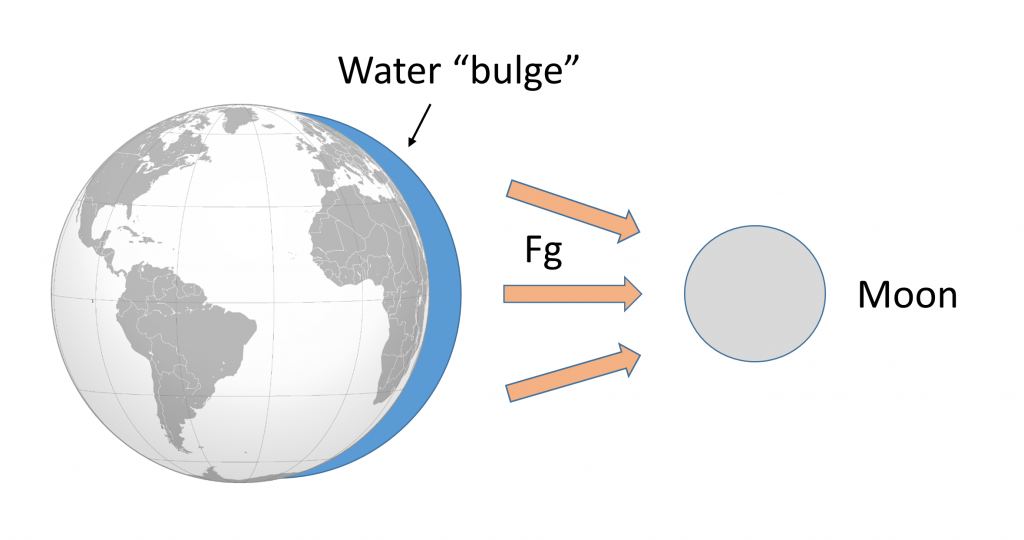
Tal fuerza gravitacional existe entre la Tierra y la luna, intentando jalarlos uno hacia el otro. Dado que el agua que cubre la Tierra es fluida (a diferencia de la tierra sólida que es más resistente a las fuerzas mareales), esta fuerza gravitacional atrae el agua hacia la luna, creando un “bulto” de agua en el lado de la Tierra frente a la luna (Figura\(\PageIndex{2}\)). Este bulto siempre mira hacia la luna, mientras que la Tierra gira a través de ella; las regiones de la Tierra que se mueven a través del bulto experimentan una marea alta, mientras que aquellas partes de la Tierra alejadas del bulto experimentan una marea baja.

Figura Las fuerzas\(\PageIndex{2}\) gravitacionales entre la Tierra y la luna provocan que aparezca una protuberancia de agua en el lado de la Tierra frente a la luna (PW).

Si las mareas fueran así de simples, en todas partes de la Tierra se vería una marea alta por día, ya que solo habría una protuberancia de agua en el lado más cercano a la luna. Sin embargo, si alguna vez has mirado las tablas de mareas, o has vivido cerca del océano, probablemente sepas que en la mayoría de los lugares hay dos mareas altas y dos bajas por día. ¿De dónde viene este segundo “bulto” de marea alta?

Podría esperarse que la fuerza gravitacional entre la Tierra y la luna acerque a los dos objetos, sin embargo, esto no está sucediendo. Esto se debe a que la fuerza gravitacional interna se opone a las fuerzas externas que mantienen separadas a la Tierra y a la Luna. La fuerza exterior es una fuerza intercial creada por la rotación de la Tierra y la Luna. Contrario a la creencia popular, la luna no está simplemente girando alrededor de la Tierra; de hecho, la Tierra y la Luna están girando una alrededor de la otra. Imagina la Tierra y la Luna como objetos de igual tamaño que giran alrededor de un punto en su centro de masa. Si ambos objetos tuvieran la misma masa, el centro de rotación sería un punto equidistante entre los dos objetos. Pero como la masa de la Tierra es 82 veces mayor que la masa de la luna, el centro de la revolución debe estar más cerca de la Tierra. Como analogía, piensa en dos personas en un balancín. Si las personas son de aproximadamente el mismo tamaño, pueden sentarse en cualquiera de los extremos de la sierra, ya que girará alrededor de un punto a igual distancia entre ellos. Pero si las dos personas tienen masas muy diferentes, como un adulto grande y un niño pequeño, la persona más grande debe acercarse al punto de pivote para que la sierra circular gire de manera efectiva. De la misma manera, el centro de rotación entre la Tierra y la luna (el baricentro) debe ubicarse más cerca de la Tierra. De hecho, el centro de rotación se encuentra dentro de la Tierra, a unos 1600 km por debajo de la superficie. A medida que la Tierra y la luna giran alrededor del baricentro, la luna viaja mucho más lejos que la Tierra, dando la impresión de que la luna está girando alrededor de la Tierra (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\) Rotación de la Tierra y la Luna alrededor del baricentro (punto blanco). Debido a su mayor masa, el centro de rotación se encuentra más cerca de la Tierra que de la luna (Por Modalanalytiker (Obra propia) [CC BY-SA 3.0 o GFDL (http://www.gnu.org/copyleft/fdl.html)], vía Wikimedia Commons).

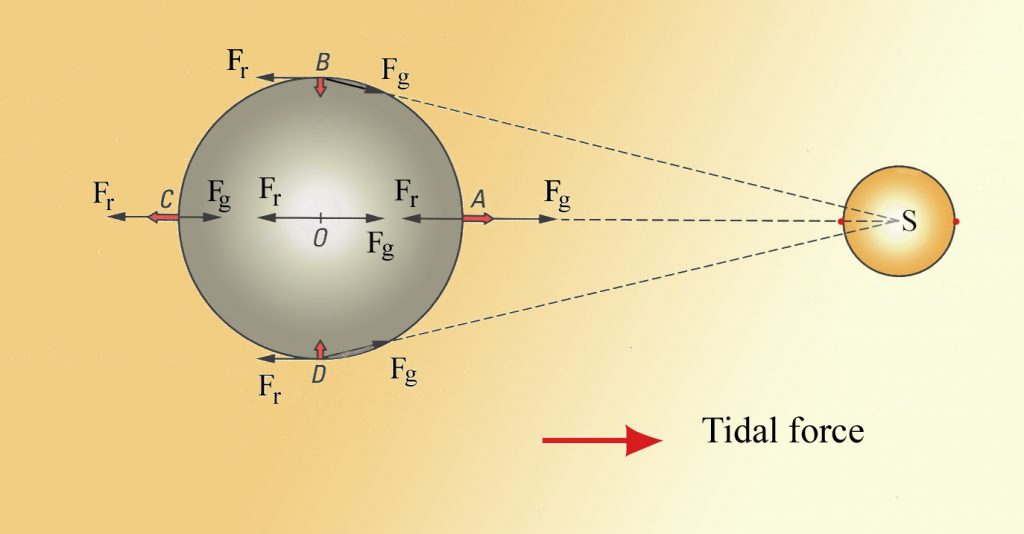
La rotación del sistema Tierra-Luna crea una fuerza inercial exterior, que equilibra la fuerza gravitacional para mantener a los dos cuerpos en sus órbitas. La fuerza inercial tiene la misma magnitud en todas partes de la Tierra, y siempre se dirige lejos de la luna. La fuerza gravitacional, por otro lado, siempre está dirigida hacia la luna, y es más fuerte en el lado de la Tierra más cercano a la luna. La figura\(\PageIndex{4}\) describe cómo se combinan estas fuerzas para crear las fuerzas mareales. En el punto O en el centro de la Tierra, la fuerza gravitacional (F _g) y la fuerza inercial (F _r) son iguales, y se cancelan entre sí. En el lado de la Tierra más cercano a la luna, la fuerza gravitacional interna (F _g) es mayor que la fuerza inercial exterior (F _r); la fuerza neta resultante (A) se dirige hacia la luna, y crea una protuberancia de agua en el lado que mira hacia la luna. En el lado de la Tierra opuesto a la luna, la fuerza inercial exterior es mayor que la fuerza gravitacional interna; la fuerza resultante neta (C) se dirige alejándose de la luna, creando una protuberancia de agua dirigida lejos de la luna.

Ahora, a medida que la Tierra gira a través de un día de 24 horas, cada región pasa por dos protuberancias, y experimenta dos mareas altas y dos mareas bajas por día. Esto representa la Teoría del Equilibrio de las Mareas de Newton, donde hay dos mareas altas y dos bajas por día, de alturas similares, cada una con seis horas de diferencia. Pero como ocurre con todo lo demás en oceanografía, la realidad es mucho más compleja que esta situación idealizada.

Figura La fuerza\(\PageIndex{4}\) gravitacional (F _g) son más fuertes más cerca de la luna y más débiles frente a la luna. Las fuerzas inerciales (F _r) son iguales en toda la Tierra y se dirigen lejos de la luna. Las fuerzas mareales A y C son el resultado de la interacción entre F _g y F _r y crean protuberancias de agua en ambos lados de la Tierra, lo que lleva a dos mareas altas por día (Vitold Muratov (Obra propia) [CC BY-SA 3.0], vía Wikimedia Commons).

Parte de la complejidad adicional se debe a que además de la luna, el sol también ejerce fuerzas que afectan a la marea en la Tierra. Las fuerzas gravitacionales e inerciales solares surgen por las mismas razones descritas anteriormente para la luna, pero las magnitudes de las fuerzas son diferentes. El sol es 27 millones de veces más masivo que la luna, pero está 387 veces más lejos de la Tierra. A pesar de su mayor masa, debido a que el sol está mucho más lejos que la luna, las fuerzas gravitacionales del sol son solo aproximadamente la mitad de fuertes que las de la luna (recuerde que la distancia está cúbica en la ecuación de gravedad). El sol crea así sus propias protuberancias de agua más pequeñas, independientes de las de la luna, que contribuyen a la creación de mareas.

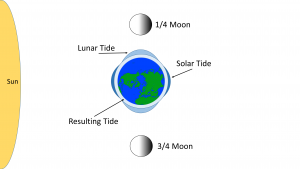
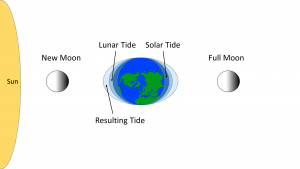
Cuando el sol, la Tierra y la luna están alineados, como ocurre durante las lunas nuevas y llenas, también se alinean los bultos solar y lunar, y se suman entre sí (interferencia constructiva; ver sección 10.2) creando un rango de mareas especialmente alto; mareas altas altas y mareas bajas bajas (Figura\(\PageIndex{5}\)). Este periodo de rango máximo de mareas se llama marea primaveral, y ocurren cada dos semanas.

Figura Las mareas de\(\PageIndex{5}\) primavera con rangos de mareas altos ocurren cuando las mareas solar y lunar se suman durante lunas llenas y nuevas cuando la Tierra, el sol y la luna están alineadas (PW).

Cuando el sol, la Tierra y la luna están a 90 ^o entre sí, las protuberancias solares y lunares están desfasadas, y se cancelan entre sí (interferencia destructiva). Ahora el rango de mareas es pequeño, con mareas bajas altas y altas bajas (Figura\(\PageIndex{6}\)). Estas son mareas neap, y ocurren cada dos semanas, cuando la luna está en sus fases 1/4 y 3/4 (Figura\(\PageIndex{7}\)).

Figura Las mareas\(\PageIndex{6}\) Neap se crean durante 1/4 y 3/4 lunas cuando la Tierra, el sol y la luna son perpendiculares entre sí. Las mareas solar y lunar se cancelan entre sí, lo que resulta en un pequeño rango de mareas (PW).

Figura\(\PageIndex{7}\) 30 días de datos de mareas de Bridgeport, CT, EE. UU., mostrando rangos de marea primaveral y neap (Modificado por PW de Cody Logan (clpo13), Dominio Público vía Wikimedia Commons).