4.2: Flujo laminar hacia abajo en un plano inclinado

En esta sección aplicamos la segunda ley de Newton al flujo estable y uniforme hacia abajo por un plano inclinado. La estrategia es observar un bloque del flujo, delimitado por planos imaginarios normales al fondo, con ancho de flujo transversal unitario y distancia de flujo unitario (Figura\(\PageIndex{1}\)). En la dinámica de fluidos, se dice que tal bloque de líquido es un “cuerpo libre”. Debido a que se supone que el flujo es constante y uniforme, todas las fuerzas en la dirección de la corriente que se ejercen sobre el fluido dentro del cuerpo libre en cualquier momento dado deben sumarse para ser cero.

Debo mencionar de entrada que por ahora no voy a abordar cómo se arregla el flujo para que el flujo sea uniforme. Si simplemente vierte una lámina de agua sobre el plano a lo largo de alguna línea horizontal particular en el plano, no debe esperar que se establezca automáticamente un flujo uniforme pendiente descendente de esa línea en el sentido de que la profundidad del flujo es la misma en todas las secciones normales a flujo más abajo del plano, y en general no lo es: necesitarías ajustar la pendiente del plano para alcanzar un estado de uniformidad. Esto no es un problema trivial, y debería esperar algún material más detallado, más adelante en este capítulo, sobre la resistencia al flujo. Por otro lado, debería tener sentido intuitivo para ti que si el avión es muy largo el grado de no uniformidad sería muy pequeño cualquiera que sea la pendiente: solo imagínate verter agua de una fila de pequeños grifos sobre un avión de una milla de largo e inclinarse unos grados.

Obviamente solo los líquidos, no los gases, pueden fluir como flujos de canal abierto. La superficie superior libremente deformable del líquido, llamada superficie libre, está abierta al aire. Desatenderemos las fuerzas menores que ejerce el aire suprayacente sobre el líquido en movimiento. Nuestro flujo de canal idealizado es de ancho infinito, sin límites laterales, y por lo tanto es solo una abstracción conveniente. Pero un flujo en un canal de sección transversal rectangular con el ancho de flujo mucho mayor que la profundidad de flujo es una buena aproximación a un flujo con ancho infinito.

Tomar la\(x\) dirección para estar aguas abajo y la dirección y para ser normal al límite, con\(y = 0\) en la parte inferior del flujo (Figura 4-1). Por la condición antideslizante, la velocidad es cero a\(y = 0\), por lo que la velocidad debe aumentar hacia arriba en el flujo. También es claro que el flujo está en todas partes dirigido directamente por el plano. Piense en las fuerzas que actúan sobre el fluido contenido en un instante dado en el cuerpo libre dentro del volumen rectangular formado por la superficie libre, el límite inferior, y dos pares de planos imaginarios normales al fondo y con espaciamiento unitario, un par paralelo al flujo y espaciados una distancia\(B\) aparte, y el otro normal al flujo y espaciado una distancia\(L\) entre sí (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Esbozo de definición para derivar el esfuerzo cortante límite en flujo uniforme constante hacia abajo de un plano inclinado.

Escribir la segunda ley de Newton para el equilibrio de fuerzas sobre este cuerpo libre significa equiparar la fuerza impulsora de la pendiente descendente, causada por el componente de pendiente descendente del peso del fluido en el cuerpo libre, con la fuerza de resistencia ejercida por el límite plano en la superficie inferior del cuerpo libre. El peso del fluido en el cuerpo libre es\(\gamma B L d\), donde\(d\) está la profundidad del flujo. El componente de pendiente descendente de este peso es\(\gamma \sin \alpha B L d\), donde\(\alpha\) está el ángulo de pendiente del plano (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Fuerzas sobre un cuerpo libre de fluido en flujo uniforme constante hacia abajo por un plano inclinado.

Esto se equilibra con la fuerza de fricción\(\tau_{\text{o}} B L\) ejercida por el límite inferior. También hay fuerzas de presión que actúan paralelas a la dirección del flujo en las caras aguas arriba y aguas abajo del cuerpo libre, pero debido a nuestra suposición de uniformidad la distribución vertical de estas fuerzas de presión es la misma en cada sección transversal, se equilibran entre sí y no causan ninguna fuerza neta sobre el cuerpo libre. Establecer\(\gamma \sin \alpha B L d\) igual a\(\tau_{\text{o}} B L\) y resolver para\(\tau_{\text{o}}\),

\[\tau_{\text{o}}=\gamma d \sin \alpha \label{4.1} \]

por lo que la tensión cortante límite es directamente proporcional al producto de la profundidad de flujo, el peso específico del líquido y el seno del ángulo de pendiente.

Figura\(\PageIndex{3}\): Croquis de un canal abierto rectangular de ancho b, para ayudar en la definición del radio hidráulico.

Antes de continuar con el desarrollo, haremos que la ecuación de resistencia sea más relevante para el mundo real escribiendo una ecuación similar para un canal con sección transversal rectangular y luego para un canal con sección transversal arbitraria (pero invariable). Para generalizar la Ecuación\ ref {4.1} a un canal rectangular, tome el ancho de flujo a ser\(b\) (Figura\(\PageIndex{3}\)) y escriba el balance de fuerzas para un cuerpo libre que llene el canal, de pared a pared, en un segmento de longitud a\(L\) lo largo del flujo. Hacer las mismas matemáticas que arriba da el resultado

\[\tau_{o}=\gamma \sin \alpha \frac{b d}{2 d+b} \label{4.2} \]

Figura\(\PageIndex{4}\): El perímetro humedecido de un flujo recto de canal abierto.

Para generalizar la Ecuación\ ref {4.1} a un canal de forma transversal arbitraria, supongamos que el área de la sección transversal es\(A\) y el perímetro humedecido (la distancia a lo largo de la parte sumergida del límite desde la línea de flotación hasta la línea de flotación) es\(P\) (Figura\(\PageIndex{4}\)). El mismo equilibrio de fuerzas da

\[\tau_{\text{o}}=\gamma \sin \alpha \frac{A}{P} \label{4.3} \]

Las ecuaciones\ ref {4.1},\ ref {4.2}, y\ ref {4.3} se ven bastante diferentes, pero se pueden unificar fácilmente definiendo una cantidad llamada radio hidráulico\(R_{H}\) formado dividiendo el área de la sección transversal del flujo por el perímetro humedecido. Puedes verificar por ti mismo que el radio de flujo hidráulico en un canal rectangular es\(b d /(2 d+b)\). Es un poco más difícil ver que el radio hidráulico de un flujo de canal infinitamente ancho es solo la profundidad del flujo\(d\). Se puede razonar que a medida que el ancho\(b\) aumenta en relación con la profundidad\(d\), el término\(2d\) en el denominador\(2d+b\) se convierte en una parte cada vez más pequeña del denominador, por lo que el radio hidráulico\(bd/(2d+b)\) tiende hacia\(bd/b\), o simplemente\(d\), a medida que el ancho aumenta relativo a la profundidad. Los lados de la derecha de las tres ecuaciones,\ ref {4.1},\ ref {4.2}, y\ ref {4.3}, se convierten\(\gamma \sin \alpha R_{H}\).

La ecuación\ ref {4.3}, o sus casos especiales La ecuación\ ref {4.1} o la ecuación\ ref {4.2}, es la ecuación de resistencia básica para un flujo uniforme constante en un canal abierto. ¡No muchos resultados útiles en mecánica de fluidos se derivan tan fácilmente! Es la principal manera en que el esfuerzo cortante límite se encuentra en los ríos (aunque para usarlo de esa manera se necesita hacer alguna topografía para establecer la elevación de la superficie del agua en dos puntos a lo largo del canal, al menos cientos si no miles de metros de distancia). En ocasiones las tres ecuaciones se escriben en términos de la pendiente\(\tan \alpha\),, más que el seno del ángulo de pendiente\(\sin \alpha\),, porque para muy pequeñas\(\alpha\) (el caso habitual), la aproximación\(\sin \alpha \approx \tan \alpha\) es buena.

Ahora volvamos al flujo infinitamente ancho por un plano: ahora que ya sabe cómo encontrar la tensión cortante límite, ¿qué se puede decir de cómo la tensión cortante y la velocidad de flujo dentro del flujo varían con la altura por encima del fondo? Una cosa que ya sabes con certeza: por la condición de antideslizante, la velocidad en la parte inferior debe ser cero. Otra cosa que se puede decir sin más derivación es que la velocidad debe estar en su máxima en la superficie libre. ¿Por qué? Porque la fuerza impulsora de la gravedad en pendiente descendente es una “fuerza corporal” que actúa a lo largo del flujo, mientras que la fuerza de fricción de resistencia actúa solo en la parte inferior. Por lo tanto, la velocidad del flujo debe aumentar monótonamente hacia arriba en el flujo.

Figura\(\PageIndex{5}\): Esbozo de definición para derivar la distribución del esfuerzo cortante en flujo laminar uniforme estable de canal abierto.

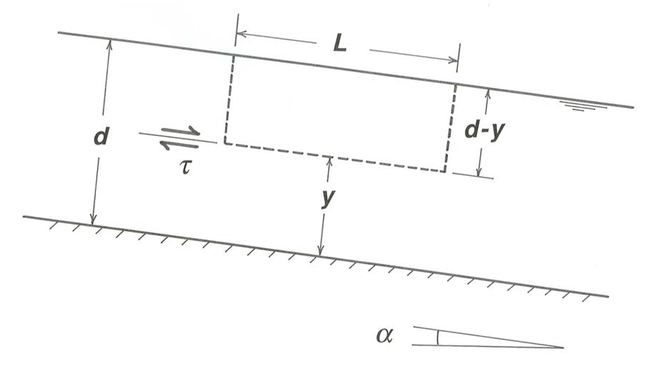
Podemos encontrar el esfuerzo cortante y la velocidad en todos los puntos arriba del flujo aplicando el mismo procedimiento de equilibrio de fuerza a un cuerpo libre de fluido similar al utilizado arriba pero con su cara inferior formada por un plano imaginario a una distancia variable por\(y\) encima del fondo y paralela a éste (Figura\(\PageIndex{5}\)). El esfuerzo cortante\(\tau\) a través del plano viene dado directamente por el equilibrio de fuerzas:

\[\tau=\gamma \sin \alpha(d-y) \label{4.4} \]

Usando la Ecuación\ ref {4.1} para eliminar\(\gamma \sin \alpha\) de la Ecuación\ ref {4.4}, podemos escribir\(\tau\) en términos de la tensión cortante límite\(\tau_{\text{o}}\):

\[\tau=\tau_{\text{o}}\left(1-\frac{y}{d}\right) \label{4.5} \]

La ecuación\ ref {4.5} muestra que\(\tau\) varía linealmente desde un máximo de\(\gamma \sin \alpha\) en la parte inferior a cero en la superficie (Figura 4-6).

Figura\(\PageIndex{6}\): Distribución del esfuerzo cortante en flujo laminar uniforme y estable de canal abierto. (Se señala más adelante en el texto que esta distribución se mantiene también para el flujo turbulento.)

Eliminando\(\tau\) de la Ecuación\ ref {4.4} mediante el uso de la Ecuación 1.3.6 da una expresión para el gradiente de velocidad\(du/dy\):

\(\mu \frac{d u}{d y}=\gamma \sin \alpha(d-y)\)

\[\frac{d u}{d y}=\frac{\gamma \sin \alpha}{\mu}(d-y) \label{4.6} \]

La ecuación\ ref {4.6} se puede integrar para dar la distribución de velocidad desde el límite inferior hasta la superficie libre:

\(\begin{aligned} u &=\int \frac{d u}{d y} d y \\ &=\int \frac{\gamma \sin \alpha}{\mu}(d-y) d y \\ &=\frac{\gamma \sin \alpha}{\mu}\left(d \int d y+\int y d y\right) \\ &=\frac{\gamma \sin \alpha}{\mu}\left(y d+\frac{1}{2} y^{2}\right)+c \end{aligned}\)

Podemos evaluar la constante de integración\(c\) mediante el uso de la condición límite que\(u = 0\) en\(y = 0\); encontramos que\(c = 0\), así

\[u=\frac{\gamma \sin \alpha}{\mu}\left(y d+\frac{1}{2} y^{2}\right) \label{4.7} \]

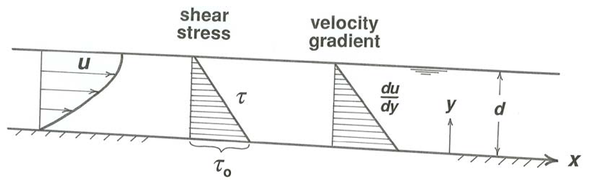
Para valores dados de\(\gamma\),\(\alpha\),\(\mu\), y\(d\), la velocidad\(u\) por lo tanto varía parabólicamente desde cero en el límite inferior hasta un máximo en la superficie (Figura\(\PageIndex{7}\)). Por otro lado, a partir de la Ecuación\ ref {4.7} el gradiente de velocidad\(du/dy\) varía linealmente desde un máximo en la parte inferior hasta cero en la superficie libre, debido a que es directamente proporcional al esfuerzo cortante (Figura\(\PageIndex{7}\)).

Figura\(\PageIndex{7}\): Distribución vertical de velocidad, esfuerzo cortante y gradiente de velocidad en flujo laminar uniforme estable de canal abierto.

Aquí hay un recordatorio sobre el cizallamiento dentro de un fluido que fluye, que encontró por primera vez en el Capítulo 1. Se puede pensar, vagamente, en términos de capas del fluido que se deslizan unas junto a otras. Una buena manera de hacer ese concreto es obtener una libreta telefónica muy gruesa y “rack” sus páginas poniéndote las manos firmemente en las portadas frontal y posterior y deslizándolas paralelas entre sí en la dirección perpendicular al lomo del libro. En los fluidos, por supuesto, el cizallamiento es continuo más que en forma de capas discretas.